Головна ⇒ 📌Формули й таблиці ⇒ Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Формули й таблиці
МАТЕМАТИКА
ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Первісна функція
Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х 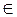 (а;b), що дорівнює f(x): F'(x) = f(x).
(а;b), що дорівнює f(x): F'(x) = f(x).
Загальний вигляд первісної F(x) + C, де С – довільне стале число.
Теорема.
Будь-яка неперервна на функція y = f(x) має первісну функцію.
Визначений інтеграл: 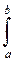 F(x)dx.
F(x)dx.
Формула Ньютона-Лейбніца:
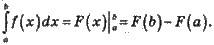
Застосування визначеного інтеграла:
1. Обчислювання площ плоских фігур
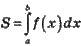
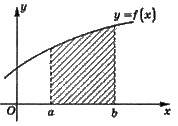
2. Обчислювання об’ємів тіл
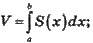
S(x) – площа перерізу 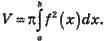
3. Обчислення відстані за відомим законом зміни швидкості: 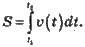
4. Обчислення роботи змінної сили: 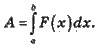
5. Обчислення кількості електрики: 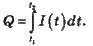
Related posts:
- Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Похідна функція – визначення похідної функції. Рівняння дотичної до графіка функції y = f(x) у точці М(х0,у0): – кутовий коефіцієнт дотичної....
- Показникова функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Показникова функція У = ах (0 < а < 1) У = ах (а > 1) Область визначення Х (-∞;+∞) Х (-∞;+∞) Множина значень Y (0;+∞) Y (0;+∞) Перетин з віссю Y При х = 0, y = 1. При х = 0, y = 1. Монотонність Функція спадає […]...
- Логарифмічна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Логарифмічна функція Y = logax(0 < a < 1) У = logax(а > 1) Область визначення Х (0;+∞) Х (0;+∞) Множина значень Y (-∞;+∞) Y (-∞;+∞) Перетин з осями координат З віссю ОХ Х = 1, у = 0; Х = 1, у = 0; З віссю OY Перетину […]...
- Інтеграл і його застосування Математика – Алгебра Нехай – неперервна функція, невід’ємна на відрізку . Розіб’ємо відрізок на n рівних частин точками , де . Утворимо добутки , і так далі й знайдемо їх суму . Знайдемо . Ця границя називається Інтегралом функції від A до B. Позначення: , де a – нижня межа інтегрування, b – верхня межа; […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Обернені тригонометричні функції – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ У = sin x 0; π/2 π/2 π/2; π π π; 3π/2 3π/2 3π/2; 2π 2π M A X П E P E Т И Н И M I N П E P E Т И Н И У = cos x 0; π/2 π/2 π/2; π π π; […]...
- Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...
- Формули приведення – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули приведення π/2 ± α π ± α 3 π/2 ± α 2π ± α 90° ± α 180° ± α 270° ± α 360° ± α Sin β Cosα Sinα -cosα ±sinα Cos β Sinα -cosα ±sinα Cosα Tg β Tgα ctgα Tgα Tgα ctgα ±tgα Ctg β […]...
- Тригонометричні функції числового аргументу Математика – Алгебра Тригонометричні функції Тригонометричні функції числового аргументу Розглянемо одиничне (тригонометричне) коло, центр якого розташований у точці і радіус якого дорівнює 1 (див. рисунок). Нехай точка P0 – це точка (1; 0). Кожну іншу точку кола можна дістати поворотом P0 навколо початку координат. Будемо вважати від’ємним напрямок повороту за годинниковою стрілкою, додатним – проти. […]...
- Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах2+bx+c. Розв’язування квадратних нерівностей” УРОК № 26 Тема. Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах 2 + b х + С. Розв’язування квадратних нерівностей” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Функція та її властивості” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. […]...
- Площі фігур Геометрія Площі фігур Геометричну фігуру називають Простою, якщо її можна розбити на скінченну кількість плоских трикутників. Для простих фігур Площа – це додатна величина, числове значення якої має такі властивості: – рівні фігури мають рівні площі; – якщо фігура розбивається на частини, що є простими фігурами, то площа цієї фігури дорівнює сумі площі її частин; […]...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- Обернені тригонометричні функції: у = arctg x, у = arcctg x УРОК 19 Тема. Обернені тригонометричні функції: у = arctg x, у = arcctg x Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arctg х і у = arcctg x. І. Перевірка домашнього завдання 1. Фронтальна бесіда з класом за питаннями 6, 7, 9-12, до “Запитання і завдання для повторення” розділу II. 2. Самостійна робота. […]...
- Значення функцій деяких кутів – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Значення функцій деяких кутів α 0; 2π π/6 π/4 π/3 π/2 π 3π/2 0; 360° 30° 45° 60° 90° 180° 270° Sin α 0 1/2 /2 /2 1 0 -1 Cos α 1 /2 /2 1/2 0 -1 0 Tg α 0 1/ 1 Не існують 0 Не існують […]...
- Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...
- Функція. Область визначення функції. Область значень функції Урок № 60 Тема. Функція. Область визначення функції. Область значень функції Мета: закріпити термінологію, відпрацювати навички роботи з поняттями функції; відпрацювати навички роботи із функцією, заданою формулою і таблично; знаходити функції аргументу, області визначення функції. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (традиційно) II. Перевірка домашнього завдання @ Оскільки основна частина […]...
- Степеневі функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції Графіки функції є параболами степеня n Графіки функції є гіперболами Функція y = ах, де а > 0, а ≠ 1, називається показниковою функцією з основою а. Приклад 0 < а < 1 Y = (1/2)x А > 1 Y = 2х Область визначення Х […]...
- Функція. Область визначення і область значень функції. Способи задання функцій. Функціональна залежність між величинами як математична модель Розділ 2. ФУНКЦІЇ & 19. Функція. Область визначення і область значень функції. Способи задання функцій. Функціональна залежність між величинами як математична модель У житті ми часто стикаємося із залежностями між різними величинами. Наприклад, периметр квадрата залежить від довжини його сторони, площа прямокутника від його вимірів, маса шматка крейди – від його об’єму, відстань, яку долає […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- Степеневі функції з раціональними показниками – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції з раціональними показниками...
- ПОНЯТТЯ ФУНКЦІЇ Розділ 4 Табличний процесор & 16. Використання вбудованих функцій 16.1. ПОНЯТТЯ ФУНКЦІЇ Ознайомимося ще з одним інструментом електронних таблиць, що дозволяє прискорити виконання обчислень, а саме із вбудованими функціями. Функція – це заздалегідь визначена формула, згідно з якою виконуються обчислення за заданими величинами у вказаному порядку. Наприклад, у таблиці наведено обсяги файлів деякої папки (рис. […]...
- Функція. Область визначення та область значень функції Урок № 61 Тема. Функція. Область визначення та область значень функції Мета: вдосконалювати та поглиблювати вміння та навички розв’язувати основні види завдань для функції, заданої формулою. Тип уроку: застосування знань. Хід уроку I. Організаційний момент II. Перевірка домашнього завдання 1) № 1,2 перевіряємо, зібравши зошити, № 2 бажано розібрати (навести приклади і сформулювати основну ідею, […]...
- ФУНКЦІЯ. СПОСОБИ ЗАДАННЯ ФУНКЦІЇ Цілі: – навчальна: сформувати поняття функції, аргументу та значення функції; домогтися засвоєння способів задання функції; сформувати вміння розв’язувати задачі, які передбачають застосування цих понять; – розвивальна: формувати культуру усного та писемного мовлення; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, працьовитість; Тип уроку : засвоєння нових знань, […]...
- Лінійні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Лінійні функції...
- Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції УРОК № 19 Тема. Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції Мета уроку: закріпити знання учнів про означення поняття нулів функції, проміжків знакосталості, функції, що зростає або спадає на проміжку, а також про способи відшукання названих характеристик функції у випадках, якщо функція задана графічно або аналітично. Закріпити вміння учнів виконувати дії […]...
- Квадратична функція – Функції та графіки Математика – Алгебра Функції та графіки Квадратична функція Квадратним тричленом називається многочлен виду , де x – змінна, a, b і c – деякі числа, причому . Коренем квадратного тричлена називається таке значення змінної, яке перетворює квадратний тричлен на 0. Щоб знайти корені квадратного тричлена, треба розв’язати квадратне рівняння . Теорема. Якщо і – корені […]...
- Квадратичні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Квадратичні функції Графіком квадратичної функції є парабола, яка отримується з графіка функції у = ах2 за допомогою двох паралельних перенесень: – перенесення уздовж осі ОХ на m одиниць ліворуч, якщо m < 0, і праворуч, якщо m > 0; – перенесення уздовж осі OY на у0 одиниць […]...
- Площа. Площа прямокутника УРОК 59 Тема. Площа. Площа прямокутника Мета: вдосконалити знання учнів про поняття площа і площа прямокутника; навчити застосовувати знання про площу прямокутника та її властивості під час розв’язування задач на комбінації геометричних фігур. Тип уроку: застосування та вдосконалення знань, умінь та навичок. Хід уроку І. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Скільки […]...
- Тригонометричні функції кута УРОК 5 Тема. Тригонометричні функції кута Мета уроку: повторити означення тригонометричних функцій гострого кута прямокутного трикутника і ввести означення тригонометричної функції довільного кута. І. Аналіз помилок, допущених у математичному диктанті та самостійній роботі. 1. Побудуйте графіки функцій (індивідуальні картки): А) ; б) ; в) ; г) . Відповідь: а) рис. 25; б) рис. 26; в) […]...