Головна ⇒ 📌Довідник з математики ⇒ Інтеграл і його застосування
Інтеграл і його застосування
Математика – Алгебра
Нехай 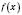 – неперервна функція, невід’ємна на відрізку
– неперервна функція, невід’ємна на відрізку 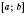 . Розіб’ємо відрізок
. Розіб’ємо відрізок 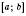 на n рівних частин точками
на n рівних частин точками 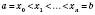 ,
,
де 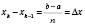 .
.
Утворимо добутки 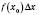 ,
, 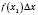 і так далі й знайдемо їх суму
і так далі й знайдемо їх суму
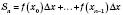
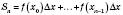 .
.
Знайдемо 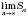 .
.
Ця границя називається Інтегралом функції
Позначення:
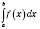 , де a – нижня межа інтегрування, b – верхня межа; функція
, де a – нижня межа інтегрування, b – верхня межа; функція 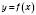 – підінтегральна функція, вираз
– підінтегральна функція, вираз 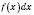 – підінтегральний вираз, x – змінна інтегрування.
– підінтегральний вираз, x – змінна інтегрування.Отже,
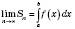 .
.Криволінійна трапеція – це фігура, обмежена графіком неперервної і невід’ємної на відрізку
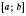 функції
функції 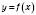 , відрізком
, відрізком 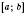 і прямими
і прямими 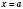 і
і 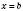 .
.Площа такої
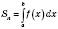 .
.Формула Ньютона – Лейбніца
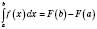 , де
, де 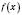 – функція, неперервна на відрізку
– функція, неперервна на відрізку 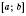 , а
, а 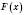 – довільна первісна для
– довільна первісна для 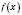 на
на 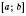 . Цю формулу можна записати у вигляді
. Цю формулу можна записати у вигляді 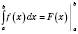 .
.
Властивості інтеграла
1. 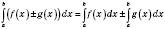 .
.
2. 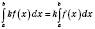 , де k Є R.
, де k Є R.
3. 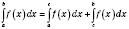 , де
, де 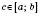 .
.
4. 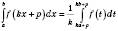 , де p Є R, k Є R.
, де p Є R, k Є R.
Обчислення площ плоских фігур за допомогою інтеграла
Нехай є яка-небудь фігура, обмежена графіком функцій 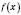 і
і 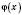 . Якщо обидві функції
. Якщо обидві функції 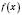 і
і 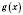 неперервні на відрізку
неперервні на відрізку 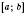 , причому
, причому 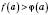 ,
, 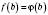 , а для всіх
, а для всіх 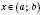 ,
, 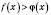 , то площа такої фігури дорівнюватиме
, то площа такої фігури дорівнюватиме 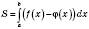 .
.




 (1 votes, average: 5.00 out of 5)
(1 votes, average: 5.00 out of 5)Related posts:
- Поняття первісної функції – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Поняття первісної функції Первісною для даної функції на заданому проміжку називається така функція , що для всіх . Операція знаходження первісної F для даної функції називається Інтегруванням. Теорема 1. Будь-яка неперервна на відрізку функція має первісну функцію. Лема. Якщо на деякому проміжку, то на цьому проміжку, де C […]...
- Інтеграл та його застосування 175. 1) F(x) = 9×2 – 2х +1? F(x) – первісна для функції у = f(x) на заданому проміжку, якщо для всіх x з цього проміжку виконується співвідношення F'(x) = f(x). Дійсно, F'(x) = 18х – 2 = 2(9х – 1) = f(x), -∞ < х < +∞, що й треба було довести. 2) Аналогічно. […]...
- Правила знаходження первісних – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Правила знаходження первісних 1. Якщо є первісною для , а – первісною для , то є первісною для. 2. Якщо є первісною для , а k – стале число, то є первісною для . 3. Якщо є первісною для , а k і b – сталі, причому , […]...
- Застосування похідної Математика – Алгебра Похідна Застосування похідної Нехай функція визначена на проміжку і . Функція називається Зростаючою в точці, якщо існує інтервал , де , який міститься у проміжку і є таким, що для всіх x з інтервалу і для всіх x з інтервалу . Функція називається Спадною в точці, якщо існує інтервал , який міститься […]...
- Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Первісна функція Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х (а;b), що дорівнює f(x): F'(x) = f(x). Загальний вигляд первісної F(x) + C, де С – довільне стале число. Теорема. Будь-яка неперервна на функція y = f(x) […]...
- Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
- Неперервність функції в точці Математика – Алгебра Границя Неперервність функції в точці Нехай функція визначена на проміжку і точка є внутрішньою точкою цього проміжку. Функція називається Неперервною в точці, якщо існує границя функції в цій точці й вона дорівнює значенню функції в точці . Нехай функція визначена в усіх точках деякого проміжку . Візьмемо дві довільні точки з цього […]...
- Кoрінь n-го степеня та його властивості Математика – Алгебра Степенева функція Кoрінь n-го степеня та його властивості Коренем N-го степеня з числаА називається таке число, n-й степінь якого дорівнює а. Якщо n – число непарне, то існує – і до того ж тільки один – корінь n-го степеня з довільного числа а. Цей корінь – число того ж знака, що число […]...
- Функції Математика – Алгебра Функції Функціональною відповідністю, або Функцією, називають таку відповідність між двома змінними, коли кожному значенню однієї змінної відповідає одне значення другої змінної. Першу змінну називають Незалежною, або Аргументом функції, а другу – Залежною, або Функцією від першої змінної. Усі значення, які приймає незалежна змінна, утворюють Область визначення функції. Записують: , де x – […]...
- Графік функції. Графічний спосіб задання функції Розділ 2. ФУНКЦІЇ & 20. Графік функції. Графічний спосіб задання функції У 6 класі ми вже розглядали графік залежності між двома величинами. Розглянемо поняття графіка функції. Приклад 1. Нехай дано функцію у = + 3, де -2 ≤ х ≤ 3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю: Х […]...
- Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...
- Застосування властивостей показникової функції до розв’язування вправ УРОК 44 Тема. Застосування властивостей показникової функції до розв’язування вправ Мета уроку. Формування умінь учнів застосовувати властивості показникової функції до розв’язування вправ. Познайомити учнів з використанням показникової функції під час вивчення явищ навколишнього середовища. І. Перевірка домашнього завдання Колективне обговорення № 1-12 із “Запитання і завдання для повторення” § 1 розділу IV. II. Набуття умінь […]...
- Відрізок і його довжина § 1. Найпростіші геометричні фігури та їхні властивості 2. Відрізок і його довжина Практичні завдання 20. Точки С, D, Е належать відрізку AB, а точки F, M, K не належать відрізку АВ. 21. Утворилося три відрізки АВ, ВС, АС. 22. Точка С лежить між точками А і В, а точка D – між точками В […]...
- Метод інтервалів Математика – Алгебра Границя Метод інтервалів Отже, нехай функція неперервна на інтервалі І й перетворюється на 0 у скінченній кількості точок цього інтервалу. Тоді інтервал І розбивається цими точками на інтервали, в кожному з яких зберігає незмінний знак. Щоб визначити цей знак, достатньо обчислити значення у будь-якій точці кожного такого інтервалу. Приклад Розв’язати нерівність Розглянемо […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Похідна Математика – Алгебра Похідна Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує до нуля, тобто . Функція в точці називається Диференційовною, якщо в цій точці вона має похідну . Якщо функція є диференційовною в кожній точці деякого інтервалу , то вона називається […]...
- Похідна та її застосування 127. 1) 2) 3) 4) 128. 1) Y = φ(x), 2) У = φ(x), не існує; 3) φ(1) = 0. 129. 1) f(x) = x2 + 1, x0 = -1, Δx = 0,1; Δy – ? Δy = у(х0 + Δх) – у(х0) = f( -0,9) – f(-1) = (-0,9)2 + 1 – ((-1)2 + […]...
- ЗАКОН ЗБЕРЕЖЕННЯ ТА ПЕРЕТВОРЕННЯ ЕНЕРГІЇ В МЕХАНІЧНИХ ПРОЦЕСАХ ТА ЙОГО ПРАКТИЧНЕ ЗАСТОСУВАННЯ Розділ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ &43. ЗАКОН ЗБЕРЕЖЕННЯ ТА ПЕРЕТВОРЕННЯ ЕНЕРГІЇ В МЕХАНІЧНИХ ПРОЦЕСАХ ТА ЙОГО ПРАКТИЧНЕ ЗАСТОСУВАННЯ З розглянутих прикладів випливає, що всі тіла в природі мають або потенціальну, або кінетичну енергію. Але в більшості випадків тіло (наприклад, літак у польоті) має одночасно і потенціальну, і кінетичну енергії. Суму потенціальної і кінетичної енергій […]...
- Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...
- Колообіг Оксигену в природі. Застосування кисню та його біологічна роль Тема 2 Кисень & 20. Колообіг Оксигену в природі. Застосування кисню та його біологічна роль Опанувавши цю тему, ви зможете: – пояснювати поняття “колообіг”, а також колообіг Оксигену, суть процесу фотосинтезу; – обгрунтовувати застосування кисню; – оцінювати значення кисню для життєдіяльності організмів, його біологічну роль. – Пригадайте з курсу природознавства, що вам відомо про поширення […]...
- Логарифмічна функція, її графік і властивості УРОК 56 Тема. Логарифмічна функція, її графік і властивості Мета уроку. Ознайомити учнів з логарифмічною функцією, її властивостями і графіком. І. Перевірка домашнього завдання 1. Три учні відтворюють розв’язування вправ № 13, 15, 20. 2. Розв’язування вправ, аналогічних домашнім. А) Обчисліть: ; . =====–=. ====–= 5. Б) Обчисліть . ==== 52 – 3-2 = 25 […]...
- ЗАКОН ЗБЕРЕЖЕННЯ Й ПЕРЕТВОРЕННЯ ЕНЕРГІЇ В МЕХАНІЧНИХ ПРОЦЕСАХ ТА ЙОГО ПРАКТИЧНЕ ЗАСТОСУВАННЯ Розділ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРІЯ & 54. ЗАКОН ЗБЕРЕЖЕННЯ Й ПЕРЕТВОРЕННЯ ЕНЕРГІЇ В МЕХАНІЧНИХ ПРОЦЕСАХ ТА ЙОГО ПРАКТИЧНЕ ЗАСТОСУВАННЯ Рух і взаємодія – необхідні умови існування матеріального світу. Якби вони зникли, світ перестав би існувати. Енергія як загальна характеристика руху і взаємодії не лише визначає здатність тіл виконувати роботу, а й кількісно доводить, що […]...
- Числові функції Математика – Алгебра Числові функції Залежність змінної y від змінної x називається Функцією, якщо кожному значенню x відповідає єдине значення y. x називається Аргументом, або Незалежною змінною, y – Залежною змінною, або Функцією від x. Позначення: , і т. д. Множина значень, яких набуває незалежна змінна x, називається областю визначення функції. Позначення: , і т. […]...
- Застосування палетки для знаходження площі непрямокутних фігур УРОК 62 Тема. Застосування палетки для знаходження площі непрямокутних фігур Мета: пояснити будову палетки і правила користування нею; вправляти учнів у складанні та обчисленні виразів; вдосконалювати обчислювальні навички. Обладнання: палетка, геометричні фігури, картка з тестовим завданням. ХІД УРОКУ I. Контроль і закріплення знань учнів Тестове опитування за темою “Площа фігур. Задачі на рух” Тест 1) […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Застосування алюмінію та його сплавів – МЕТАЛИ ГОЛОВНИХ ПІДГРУП ПОСІБНИК З ХІМІЇ ДЛЯ ВСТУПНИКІВ ДО ВИЩИХ НАВЧАЛЬНИХ ЗАКЛАДІВ Частина II. НЕОРГАНІЧНА ХІМІЯ Розділ 13. МЕТАЛИ ГОЛОВНИХ ПІДГРУП § 13.13. Застосування алюмінію та його сплавів Фізичні та хімічні властивості алюмінію зумовили його широке застосування в техніці. Значним споживачем алюмінію є авіаційна промисловість: літак на складається з алюмінію та його сплавів, а авіацшнии двигун – на […]...
- ЗАКОН ЗБЕРЕЖЕННЯ Й ПЕРЕТВОРЕННЯ ЕНЕРГІЇ В МЕХАНІЧНИХ ПРОЦЕСАХ ТА ЙОГО ПРАКТИЧНЕ ЗАСТОСУВАННЯ Тип уроку: комбінований урок. Мета: навчити учнів описувати перетворення кінетичної енергії в потенціальну і навпаки, наводити приклади перетворення одного виду механічної енергії в інший, пояснити сутність закону збереження енергії; формувати матеріалістичний світогляд учнів. Обладнання та наочність: досліди, що ілюструють перетворення одного виду енергії в інший, портрет Ю. Р. Майера. Відеофрагмент: стрільба з лука, фрагмент мультфільму […]...
- Функції та графіки Математика – Алгебра Функції та графіки Функція може задаватися описом, таблицею, графіком, формулою тощо. Область визначення функції зручно записувати за допомогою числових проміжків. Приклади 1) ; ; 2) ; ; 3) ; ; 4) ; . Пояснимо, як ми знайшли область визначення в останньому прикладі. Функція визначена для тих і тільки тих значень x, які […]...
- Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...
- Застосування координат 124. Б) 0 ≤ x ≤ 4; 0 ≤ у ≤ 4; 0 ≤ z ≤ 4. 125. 0 ≤ х ≤ 3; 0 ≤ у ≤ 3; -3 ≤ 2 ≤ 3. 126. А) А(0; 0; 0); В(0; 1; 0); С(1; 1; 0); D(1; 0; 0); А1(0; 0; 1); В1(0; 1; 1); С1(1; 1; […]...
- ЗМІННА НЕПЕРЕРВНА Соціологія короткий енциклопедичний словник ЗМІННА НЕПЕРЕРВНА – Див. Змінна дискретна та Змінна неперервна....
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Лінійне рівняння з двома змінними та його графік Урок № 70 Тема. Лінійне рівняння з двома змінними та його графік Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння […]...
- Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
- Умови виникнення й припинення горіння. Поширення та колообіг Оксигену в природі. Застосування кисню, його біологічна роль ТЕМА 2. ПРОСТІ РЕЧОВИНИ МЕТАЛИ І НЕМЕТАЛИ Урок 4. Умови виникнення й припинення горіння. Поширення та колообіг Оксигену в природі. Застосування кисню, його біологічна роль Цілі: вивчити умови виникнення й припинення горіння, кругоообіг Оксигену в природі; формувати знання про реакції горіння на прикладах горіння складних речовин, про оксиди; з’ясувати галузі застосування кисню. Обладнання: таблиці “Застосування […]...
- ВЛАСТИВОСТІ ТА ВИГОТОВЛЕННЯ ДРОТУ, ВИДИ ДРОТУ ТА ЙОГО ЗАСТОСУВАННЯ РОЗДІЛ 1 ОСНОВИ МАТЕРІАЛОЗНАВСТВА ВИДИ ТА ПРИЗНАЧЕННЯ КОНСТРУКЦІЙНИХ МАТЕРІАЛІВ. ТОНКОЛИСТОВИЙ МЕТАЛ ТА ДРІТ § 5. ВЛАСТИВОСТІ ТА ВИГОТОВЛЕННЯ ДРОТУ, ВИДИ ДРОТУ ТА ЙОГО ЗАСТОСУВАННЯ Опорні поняття: дріт; прокатування та волочіння дроту; електричний та конструкційний дріт; застосування дроту. – Дріт – металевий виріб у вигляді гнучкої нитки або тонкого прута. Дріт, як правило, круглого, рідше – […]...
- Застосування векторів 269. 5(х – 2) + 0 × (у + 1) – 3(z – 4) = 0; 5x – 10 – Зz + 12 = 0; 5x – Зz + 2 = 0 – рівняння шуканої площини. 270. 3(x – 1) – 4(y – 2) + 7(z + 3) = 0; 3x – 3 – 4у […]...
- Перетворення многочлена на квадрат суми або різниці двох виразів 624. а2 – 18а + 81 = (а – 9)2. 625. Тотожністю є рівність 2) а2 + 8аb + 16b2 = (а + 4b)2. 628. 1) Якщо у = -4, то у2 – 8у + 16 = (у – 4)2 = (-4 – 4)2 = 64. 2) Якщо с = -10, то с2 + 24с […]...
- Розв’язування задач на застосування векторів Урок 60 Тема. Розв’язування задач на застосування векторів Мета уроку: формування вмінь учнів застосовувати вивчений матеріал до розв’язування задач. Обладнання: стінна таблиця “Вектори в просторі”. Хід уроку І. Перевірка домашнього завдання 1. Два учні відтворюють розв’язування задач № 55 (4), 56. 2. Фронтальне опитування. 1) Чому дорівнює скалярний добуток векторів, які задано координатами? 2) Як […]...