Площа ортогональної проекції многокутника
Урок 56
Тема. Площа ортогональної проекції многокутника
Мета уроку: вивчення теореми про площу ортогональної проекції многокутника, формування вмінь учнів застосовувати вивчену теорему до розв’язування задач.
Обладнання: стереометричний набір, модель куба.
Хід уроку
1. Два учні відтворюють розв’язування задач № 42, 45 на дошці.
2. Фронтальне опитування.
1) Дайте означення кута між двома площинами, які перетинаються.
2) Чому дорівнює кут між:
А) паралельними площинами;
Б) перпендикулярними площинами?
3)
4) Чи правильно, що площина, яка перетинає паралельні площини, перетинає їх під однаковими кутами?
5) Чи правильно, що площина, яка перетинає перпендикулярні площини, перетинає їх під однаковими кутами?
3. Перевірка правильності розв’язання задач № 42, 45, яке відтворили учні на дошці.
Учням пропонується самостійно прочитати в підручнику доведення теореми 4.1 із п. 34, а потім викликаються до дошки учні, які відтворюють доведення теореми.
1. Доведіть, що площа проекції трикутника, у якого одна сторона знаходиться в площині проекції, дорівнює
2. Доведіть теорему для випадку, коли многокутником є трикутник, у якого одна сторона паралельна площині проекцій.
3. Доведіть теорему для випадку, коли многокутником є трикутник, у якого жодна із сторін не паралельна площині проекцій.
4. Доведіть теорему для будь-якого многокутника.
1. Знайти площу ортогональної проекції многокутника, площа якого дорівнює 50 см2, а кут між площиною многокутника і його проекцією – 60°.
2. Знайти площу многокутника, якщо площа ортогональної проекції цього многокутника дорівнює 50 см2, а кут між площиною многокутника і його проекцією дорівнює 45°.
3. Площа многокутника дорівнює 64 см2, а площа ортогональної проекції – 32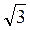
см2. Знайдіть кут між площинами многокутника і його проекцією.
4. Чи може площа ортогональної проекції многокутника дорівнювати площі цього многокутника?
5. Ребро куба дорівнює а. Знайти площу перерізу куба площиною, яка проходить через вершину основи під кутом 30° до цієї основи і перетинає всі бічні ребра. (Відповідь.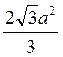 
)
6. Задача № 48 (1, 3) із підручника (с. 58).
7. Задача № 49 (2) із підручника (с. 58).
8. Сторони прямокутника дорівнюють 20 і 25 см. Його проекція на площину подібна йому. Знайти периметр проекції. (Відповідь. 72 см або 90 см.)
§4, п. 34; контрольне запитання № 17; задачі № 48 (2), 49 (1) (с. 58).
IV. Підведення підсумку уроку
Запитання до класу
1) Сформулюйте теорему про площу ортогональної проекції многокутника.
2) Чи може площа ортогональної проекції многокутника бути більшою площі многокутника?
3) Через гіпотенузу АВ прямокутного трикутника АВС проведено площину? під кутом 45° до площини трикутника і перпендикуляр CO до площини?. АС = 3 см, ВС = 4 см. Укажіть, які з наведених тверджень правильні, а які – неправильні:
А) кут між площинами АВС і? дорівнює куту СМО, де точка М – основа висоти СМ трикутника АВС;
Б) СО = 2,4
см;
В) трикутник АОС є ортогональною проекцією трикутника АВС на площину?;
Г) площа трикутника АОВ дорівнює 3 см2.
(Відповідь. а) Правильне; б) неправильне; в) неправильне; г) правильне.)
(1 votes, average: 5.00 out of 5)
Loading...