Площа прямокутника. Площа паралелограма
Урок № 45
Тема. Площа прямокутника. Площа паралелограма
Мета: закріпити знання учнів про:
– зміст та властивості площі многокутника;
– зміст теореми про площу прямокутника та його наслідок.
Сформулювати та довести теорему про площу паралелограма.
Продовжувати формувати вміння відтворювати зміст вивчених понять та теорем, а також використовувати їх під час розв’язування задач на обчислення площ прямокутника і паралелограма.
Тип уроку: засвоєння вмінь та навичок.
Наочність та обладнання: конспекти: “Площа.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Для економії часу на цьому етапі уроку учні коментують розв’язання домашніх задач за готовими рисунками, виконаними на дошці заздалегідь.
III. Формулювання мети і завдань уроку
З метою створення проблемної ситуації пропонуємо учням задачу.
Задача. Двом учням дали завдання пофарбувати два листи фанери: одному у формі прямокутника зі сторонами 3 м і 5 м, а другому – у формі паралелограма, в якому до сторони довжиною 5 м проведена висота довжиною 3
Обговорюючи завдання, учні доходять висновку, що для відповіді на запитання задачі треба знайти площі фігур, даних у задачі. Площа прямокутника обчислюється за відомою учням формулою, а обчислення площі паралелограма – є ключовим питанням. Отже, формулюється завдання – вивчити спосіб обчислення площі паралелограма за стороною та проведеною до неї висотою. Виконання цього завдання – основна мета уроку.
IV. Актуалізація опорних знань
Для успішного засвоєння учнями змісту та ідеї доведення теореми про обчислення площі паралелограма учням слід активізувати знання і вміння щодо властивостей площ; формули площі прямокутника; ознак рівності прямокутних трикутників; властивостей паралелограма; оперативних умінь роботи з формулами.
Виконання усних вправ
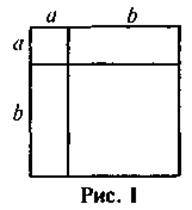
1. На рис. 1 зображено геометричне доведення формули (a + b)2 = а2 + 2ab + b2. Дайте пояснення.
2. Площа квадрата (у м2) виражається тим самим числом, що й периметр (у м). Чому дорівнює сторона квадрата?
3. Як зміниться площа прямокутника, коли одну з його сторін збільшити в 4 рази, а другу зменшити в 4 рази?
4. ОС – бісектриса кута АОВ, CD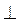 OA, CF
OA, CF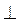 OB (рис. 2). Доведіть, що CD = CF.
OB (рис. 2). Доведіть, що CD = CF.
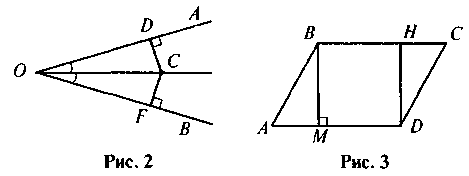
5. ABCD – паралелограм, ВМ 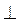 AD, DH
AD, DH 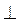 ВС (рис. 3). Доведіть, що? ABM = ?CDH.
ВС (рис. 3). Доведіть, що? ABM = ?CDH.
V. Засвоєння знань
План вивчення нового матеріалу
1. Теорема про площу паралелограма.
2*. Наслідки з формули паралелограма.
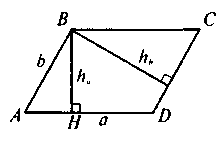
@ На цьому уроці починається робота з вивчення формул для обчислення площ чотирикутників, властивості яких було вивчено раніше, а також формули площі трикутника. Доведення теореми про формулу площі паралелограма зазвичай не становить труднощів для учнів (особливо після проведеної роботи з повторення – див. усні вправи). Запис доведення теореми можна зробити так, як це показано на рис. 4.
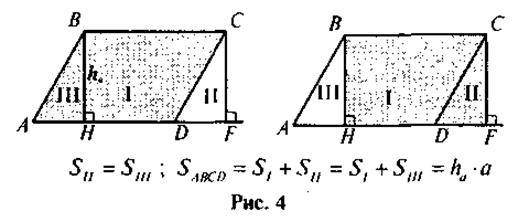
Під час роботи над закріпленням доведеної формули слід опрацювати такі контрольні моменти: для обчислення площі паралелограма береться тільки висота, проведена до даної сторони; оскільки висота паралелограма менша від його сторони (чому?), то замінювати висоту на сторону, обчислюючи площу паралелограма, не можна (на відміну від прямокутника). Також доречно обговорити застосування формули для обчислення площі ромба (оскільки висоти і сторони ромба рівні, то площу ромба можна знайти як добуток сторони на висоту). Як один із важливих наслідків з формули площі паралелограма, можна розглянути факт про те, що сторони паралелограма обернено пропорційні до його відповідних сторін (більш простий варіант формулювання цієї властивості: до більшої сторони паралелограма проведено меншу висоту, і навпаки). Що стосується інших наслідків із доведеної теореми, які традиційно вивчаються після здобуття формули S = aha, то вони вивчатимуться пізніше (після опанування учнями способів розв’язання прямокутних трикутників).
Конспект 18 | |
Площа паралелограма | |
Якщо ABCD – паралелограм, AD = a, ВН = ha – висота, проведена до AD, то SABCD = ahа (bhb) Наслідки 1) |
|
VI. Формування первинних умінь
Виконання усних вправ
1. Чи правильне міркування: “У паралелограмі ABCD довжини сторін дорівнюють а і b, а площа не дорівнює ab. Отже, цей паралелограм не прямокутник”. Чому?
2. Чи існує паралелограм, сторони якого мають довжини 3 см і 6 см, а відповідні висоти 4 см і 1 см?
3. Кожна сторона паралелограма менша за 1 м, а площа дорівнює 1 м2. Чи може так бути? Поясніть.
Виконання письмових вправ
1. У паралелограмі зі стороною а, проведеною до неї висотою ha і площею S знайдіть:
А) S, якщо a = 10 см, ha = 6 см;
Б) а, якщо S = 48 см2, ha = 4 см;
В) ha, якщо S = 120 см2, а = 24 см.
2. Діагональ паралелограма дорівнює 15 см і перпендикулярна його стороні. Знайдіть площу паралелограма, якщо інша його сторона дорівнює 17 см.
3. Знайдіть площу паралелограма, якщо:
А) його периметр дорівнює 42 см, а довжини висот складають 6 см і 8 см;
Б) його сторона дорівнює 5 см, а висота ділить іншу сторону на відрізки завдовжки 4 см і 6 см;
В) його сторони дорівнюють 8 см і 10 см, а гострий кут – 30°.
VII. Підсумки уроку
Чи правильне твердження теореми про площу паралелограма для прямокутника?
Чи правильне твердження: площа паралелограма дорівнює добутку його сторони на висоту? Для якого чотирикутника це твердження правильне?
VIII. Домашнє завдання
Вивчити зміст та доведення теореми про площу паралелограма.
Розв’язати задачі.
1. Сторони паралелограма дорівнюють 12 см і 16 см. Знайдіть його висоти, якщо площа паралелограма дорівнює 96 см2.
2. Сторона паралелограма і проведена до неї висота дорівнюють відповідно 16 см і 9 см. Знайдіть сторону квадрата, рівновеликого даному паралелограму.
3. Виріжте з паперу два рівні рівнобедрені трикутники і складіть з них:
А) ромб; б) паралелограм, відмінний від ромба.
Порівняйте площі складених фігур.
4. Знайдіть площу паралелограма, якщо:
А) його діагональ перпендикулярна стороні, а висота, проведена вершини тупого кута, ділить іншу сторону на відрізки завдовжки 4 см і 9 см;
Б) його сторони дорівнюють 4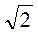 см і 8 см, а гострий кут – 45°.
см і 8 см, а гострий кут – 45°.
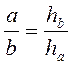 ; 2) S = ah.
; 2) S = ah.