Поділ числа у даному відношенні
Розділ 3 Відношення і пропорції
§24. Поділ числа у даному відношенні
Розглянемо задачі, в яких вимагається поділити число або значення величини у даному відношенні, тобто на частини, пропорційні деяким числам. Такі задачі називають задачами на поділ числа у даному відношенні або задачами на пропорційний поділ.
Задача 1. Сплав масою 30 кг складається із заліза і міді, які взято у відношенні 3 : 2. Скільки у сплаві заліза і скільки міді?
Розв’язання. І спосіб. (Мал. 8). Маси заліза і міді відносяться як 3 : 2, тобто до сплаву входить 3 частини

Мал. 8
Мал. 9
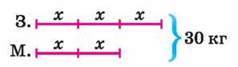
II спосіб. (Мал. 9). Позначимо масу однієї частини буквою х. Оскільки заліза взято три частини, то його у сплаві х + х + х = 3х (кг), а міді взято дві частини, тому її у сплаві х + х = 2х (кг).
За умовою маємо рівняння 3х + 2х = 30. Тоді 5х = 30. Отже, х = 6 (кг) – маса однієї частини, тобто 6 ∙ 3 = 18 (кг) – взято заліза, 6 ∙ 2 = 12 (кг) – міді.
Відповідь. 18 кг заліза і 12 кг міді.
Часто
Задача 2. Між мамою, татом і їхнім сином поділили яблука у відношенні 2 : 1 : 3. Скільки яблук отримала мама і скільки тато, якщо син отримав 12 яблук?
Розв’язання. Оскільки трьом частинам відповідають 12 яблук, то на одну частину припадає 12 : 3 = 4 (яблука). Отже, тато отримав 4 яблука, а мама – 4 ∙ 2 = 8 (яблук).
Відповідь. 4 яблука – тато, 8 яблук – мама.
– Поясни хід розв’язування задачі 1 (І спосіб і II спосіб) та задачі 2.
620. (Усно) Шапокляк і крокодил Гена грали в теніс. Кількість партій, які виграла Шапокляк, відноситься до кількості партій, які виграв Гена, як 1 : 3. Скільки партій виграла Шапокляк, якщо Гена виграв 6 партій?
621. Кількість задач, які розв’язав Юрко, відноситься до кількості задач, які він не розв’язав, як 1 : 2. Скільки задач розв’язав Юрко, якщо йому залишилося розв’язати 4 задачі?
622. Поділи:
1) число 21 на дві частини у відношенні 2 : 5;
2) число 48 на три частини у відношенні 3 : 7 : 2.
623. Поділи:
1) число 210 на дві частини у відношенні 7 : 3;
2) число 104 на три частини у відношенні 2 : 5 : 6.
624. Латунь – це сплав міді і цинку, маси яких відносяться як 3 : 2. Для виготовлення шматка латуні потрібно 240 г міді. Скільки треба взяти цинку, щоб виплавити такий шматок латуні?
625. Сплав містить 3 частини цинку і 4 частини заліза. Скільки треба взяти цинку для такого сплаву, якщо заліза взято 240 кг?
626. Для виготовлення соку беруть 3 частини фруктів і 5 частин води. Скільки фруктів треба взяти, щоб отримати 96 кг соку?
627. Периметр трикутника дорівнює 60 дм, а довжини сторін відносяться як 6 : 5 : 4. Знайди сторони трикутника.
628. Сторони трикутника відносяться як 4 : 7 : 8. Сума найбільшої і найменшої сторін дорівнює 36 см. Знайди довжину середньої сторони.
629. Сторони трикутника відносяться як 2 : 3 : 4. Різниця найбільшої і найменшої сторін дорівнює 12 см. Знайди сторони трикутника.
630. Три будівельники, які мають однакову продуктивність праці, встановлювали паркан у заміському будинку. Перший працював 5 днів по 6 годщодня, другий – 8 днів по 5 год щодня, третій – 4 дні по 7 год щодня. За встановлений паркан їм заплатили 3430 грн. По скільки гривень отримав кожен будівельник?
631. На спорудженні будинку працювало три бригади. У першій бригаді 8 робітників працювало 10 днів, у другій 10 робітників працювало 9 днів, у третій 6 робітників працювало 12 днів. За роботу всі три бригади разом отримали 31 460 грн. По скільки гривень отримала кожна бригада, якщо продуктивність праці всіх робітників однакова?

632. Поділи число 182 на три частини х, у і z так, щоб х : у = 2 : 1, у : z = 3 : 4.
633. Із 25 л молока отримують 3 л вершків. Скільки вершків отримають з 35 л молока? Скільки треба молока, щоб отримати 7,5 л вершків?
634. Спрости відношення: 1) 875 : 1125; 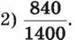
635. Однією з робіт відомого українського майстра мікромініатюр Миколи Сергійовича Сядристого, є найменша у світі скрипка, довжина якої 3,45 мм. Справжня довжина скрипки дорівнює 58-59 см. В якому масштабі (приблизно) майстер виконав свою мікромініатюру?