Головна ⇒ 📌Довідник з математики ⇒ Послідовності
Послідовності
Математика – Алгебра
Послідовності
Розглянемо яку-небудь множину, що містить 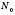 дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до
дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до 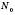 , або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад:
, або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад:
2; 4; 6; 8; … – послідовність парних чисел;
1; 3; 5; …. – послідовність непарних чисел;
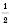
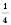 ;
; 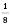 ; … – послідовність чисел вигляду
; … – послідовність чисел вигляду 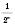 ;
;3; 6; 9; … – послідовність чисел, кратних 3.
Числа, що утворюють послідовність, називаються її Членами і позначаються буквою з індексом. Наприклад,
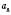 – восьмий член послідовності,
– восьмий член послідовності, 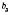 – третій член і т. д.
– третій член і т. д.Послідовності можуть бути Скінченні і Нескінченні.
Приклад скінченної послідовності: 12; 14; 16; 18; 20 – послідовність парних чисел, більших від 10, але не більших, ніж 20. Тобто:
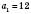
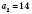 ;
; 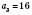 ;
; 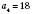 ;
; 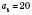 .
.Послідовність можна задавати описом, таблицею.
Найзручніший спосіб – це задати послідовність Формулою N-го члена.
Наприклад, послідовність чисел, кратних 5, можна задати формулою
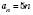 .
.Щоб знайти, наприклад, 20-й член послідовності, треба замість n підставити у формулу число 20:
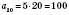 .
.Навпаки, щоб дізнатися, який номер має в цій послідовності число 80, треба скласти рівняння
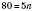 , звідки
, звідки 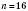 , тобто
, тобто 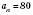 .
.У випадку рівняння
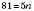 робимо висновок, що числа 81 серед членів цієї послідовності немає, тому що рівняння не має натуральних коренів.
робимо висновок, що числа 81 серед членів цієї послідовності немає, тому що рівняння не має натуральних коренів.Послідовність можна також задавати формулою, яка виражає будь-який член послідовності, починаючи з деякого, через один чи кілька попередніх.
Наприклад, нехай
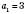 , тоді
, тоді 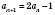 .
.Послідовність називають Зростаючою, якщо кожний її член, починаючи з другого, більший від попереднього. Послідовність називається Спадною, якщо кожний її член, починаючи з другого, менший від попереднього.
Related posts:
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Границя числової послідовності Математика – Алгебра Границя Границя числової послідовності Число a називається Границею послідовності,, …, , …, якщо для будь-якого додатного числа існує таке натуральне число , що для всіх виконується нерівність . Позначеня: , або . Послідовність , , 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що […]...
- Числові послідовності УРОК № 65 Тема. Числові послідовності Тестові завдання 1. Послідовність задано формулою аn = 5n + 2. Знайдіть а3. А) 3; б) 17; в) 5; г) інша відповідь. 2. В арифметичній прогресії (bп) різниця дорівнює 2. Знайдіть b10, якщо b1 = 3. А) 1536; б) 18; в) 21; г) інша відповідь. 3. Знайдіть суму перших […]...
- Арифметична прогресія Математика – Алгебра Послідовності Арифметична прогресія Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії. Арифметична прогресія буде зростаючою, якщо , і спадною, якщо . Прогресію можна задати за допомогою першого члена […]...
- Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю . . Теорема 2. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю, яка дорівнює ab: . Наслідки 1) Сталий множник можна виносити за знак границі. […]...
- Геометрична прогресія Математика – Алгебра Послідовності Геометрична прогресія Геометричною прогресією називається послідовність відмінних від 0 чисел, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число q називають Знаменником геометричної прогресії. Формула n-го члена геометричної прогресії: . Теорема. Послідовність тоді й тільки тоді є геометричною […]...
- Властивості прогресій – ПРОГРЕСІЇ Формули й таблиці МАТЕМАТИКА ПРОГРЕСІЇ Нескінченною числовою послідовністю називається числова функція, визначена на множині натуральних чисел: Арифметична прогресія Геометрична прогресія Арифметичною прогресією називається така послідовність чисел, при якій кожен член, починаючи із другого, дорівнює попередньому, доданому до одного й того самого, постійного для цього ряду числа. Геометричною прогресією називається така послідовність чисел, при якій кожен […]...
- Подільність цілих чисел Формули й таблиці МАТЕМАТИКА Подільність цілих чисел Ціле число а ділить ціле число b, або b ділиться на а, якщо існує таке ціле число с, при якому b = ас. Це має місце тоді, коли остача від ділення числа b на число а дорівнює нулю. Подільність цілих чисел має такі властивості: 1. Будь-яке ціле число […]...
- ОЗНАКИ ПОДІЛЬНОСТІ НА 2, 10, 5 Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ § 2. ОЗНАКИ ПОДІЛЬНОСТІ НА 2, 10, 5 Запишемо натуральний ряд чисел: 1; 2; 3; 4; 5; б; 7; 8; 9; 10; 11; 12… Помножимо кожне число на 2. Дістали ряд чисел, кратних числу 2: 2; 4; 6; 8; 10; 12; 14; 16; 18; 20; 22; 24… Такі числа називають […]...
- Дійсні числа Математика – Алгебра Квадратні корені Раціональні числа – це числа, які можуть бути записані у вигляді , де m – ціле число, n – натуральне. Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. І навпаки, кожний нескінченний періодичний десятковий дріб є раціональним числом. Числа, які зображуються нескінченними неперіодичними десятковими дробами, називають ірраціональними. […]...
- ЗАКОН ПОСЛІДОВНОСТІ ПРОХОДЖЕННЯ ФАЗ РОЗВИТКУ Екологія – охорона природи ЗАКОН ПОСЛІДОВНОСТІ ПРОХОДЖЕННЯ ФАЗ РОЗВИТКУ – фази розвитку прир. системи можуть проходити лише в еволюційно закріпленому порядку (історично, екологічно зумовленому), від відносно простого до складного, як правило, без випадання проміжних етапів (однак, можливо, з дуже швидким їх проходженням або еволюційно закріпленою відсутністю). Напр., метаморфоз комах з повним перетворенням може відбуватися лише […]...
- Множини і підмножини 567. А – (понеділок, вівторок, середа, четвер, п’ятниця, субота, неділя) – множина днів тижня; В – множина кольорів світлофора: (жовтий, зелений, червоний); С – множина материків: (Євразія, Африка, Північна Америка, Південна Америка, Австралія, Антарктида); D – множина цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; E – множина кольорів веселки (червоний, оранжевий, […]...
- Дільники і кратні Математика – Алгебра Подільність натуральних чисел Дільники і кратні Дільником натурального числа а називають натуральне число, на яке а ділиться без остачі. Кратним натуральному числу а називається натуральне число, яке ділиться на а без остачі. Приклади 1) Число 12 має 6 дільників: 1, 2, 3, 4, 6, 12. (Зверніть увагу: .) 2) Запишемо п’ять перших […]...
- Поняття рівняння. Розв’язування рівнянь 770. а) 5х = 3х + 4. Х = 2 – корінь рівняння, бo 5 • 2 = 3 • 2 + 4 – правильна рівність. Б) 2х + 8 = 7х. Х = 2 – не є коренем рівняння, 2 • 2 + 8 = 7 • 2 – неправильна рівність. В) 10 – […]...
- Практична робота “Визначення технологічної послідовності виготовлення виробу з аплікацією” Розділ 2. ОЗДОБЛЕННЯ ВИРОБІВ АПЛІКАЦІЄЮ Урок № 7 Тема. ПОСЛІДОВНІСТЬ ВИГОТОВЛЕННЯ ВИРОБУ З АПЛІКАЦІЄЮ Практична робота “Визначення технологічної послідовності виготовлення виробу з аплікацією” Мета уроку: Навчальна: забезпечити засвоєння учнями знань про технологічну послідовність виготовлення будь-якого виробу, формувати вміння планувати й виконувати технологічні операції; Розвивальна: розвивати логічне мислення, уміння аналізувати та співставляти; Виховна: виховувати потребу проявити […]...
- Прості й складені числа Математика – Алгебра Подільність натуральних чисел Прості й складені числа Натуральне число називається Простим, якщо воно має тільки два різних дільники: одиницю й саме це число. Число, яке має більше двох дільників, називається складеним. Число 1 має єдиний дільник – 1, тому не належить ні до простих, ні до складених чисел. Приклади 1) Числа 2, […]...
- Ознаки подільності на 10, 5 та 2 Розділ 1 Подільність натуральних чисел §2. Ознаки подільності на 10, 5 та 2 Припустимо, що треба дізнатися, чи ділиться число 137 146 на 5. Для цього можна виконати ділення й одержати відповідь на поставлене запитання. Але відповідь можна знайти значно простіше, не виконуючи ділення, за допомогою ознак подільності. Розглянемо деякі з них. Будь-яке натуральне число, […]...
- НАЙМЕНШЕ СПІЛЬНЕ КРАТНЕ Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ §5. НАЙМЕНШЕ СПІЛЬНЕ КРАТНЕ Знайдемо кратні числа 4. Для цього достатньо помножити число 4 на числа натурального ряду: 4; 8; 12; 16; 20; 24; 28; 32; 36; 40; 44… Аналогічно знайдемо кратні числа 6: 6; 12; 18; 24; 30; 36; 42; 48; 54; 60; 66… Серед кратних числа 4 і […]...
- Дільники і кратні натурального числа Розділ 1 Подільність натуральних чисел У цьому розділі ви: – ознайомитеся з дільниками і кратними натуральних чисел; – дізнаєтеся про прості та складені числа, взаємно прості числа; – навчитеся розкладати числа на прості множники, знаходити найбільший спільний дільник і найменше спільне кратне натуральних чисел. §1. Дільники і кратні натурального числа 15 яблук можна розділити порівну […]...
- МАТЕМАТИКА Формули й таблиці МАТЕМАТИКА Натуральні числа Натуральні – числа 1, 2, 3, що використовуються для рахунку предметів. Позначається буквою N. Просте число – натуральне число, що має тільки 2 дільники: самого себе й одиницю. Таких чисел нескінченна множина. Якщо число n – це добуток двох чисел: n = m · k, то воно ділиться без […]...
- Модуль числа Математика – Алгебра Раціональні числа Модуль числа Відстань від початку відліку до точки, що зображає число на координатній прямій, називається Модулем даного числа. Позначення: – модуль а. Очевидно, що для додатних чисел і 0 , для від’ємних . для будь-якого числа а. Модулі протилежних чисел рівні: . Приклади 1) ; ; . 2) Розв’яжіть рівняння. […]...
- Ознаки подільності натуральних чисел на 2, 5, 10, 3 і 9 Урок № 3 Тема. Ознаки подільності натуральних чисел на 2, 5, 10, 3 і 9 Мета: відпрацювати навички використання ознак подільності і понять уроку №1 для виконання завдань, що передбачають означення подільності чисел. Тип уроку: засвоєння вмінь і навичок. Хід уроку І. Перевірка домашнього завдання 1. Ігровий момент @Учитель заздалегідь виготовляє картки з правильними і […]...
- Взаємно обернені числа Розділ 2 Звичайні дроби §16. Взаємно обернені числа Розглянемо дріб і поміняємо в ньому чисельник і знаменник місцями. Отримаємо дріб Якщо тепер помножити дріб то отримаємо 1: Також отримаємо 1 при множенні 5 на тощо. – Два числа, добуток яких дорівнює 1, називають взаємно оберненими. Легко зробити висновок: щоб знайти дріб взаємно обернений з даним […]...
- Квадратні корені Математика – Алгебра Квадратні корені Квадратні рівняння Квадратним рівнянням називається рівняння виду , де х – невідоме, a, b, c – деякі числа, причому . Числа a, b, c – коефіцієнти квадратного рівняння: a – перший коефіцієнт, b – другий коефіцієнт, c – вільний член. Якщо , рівняння називається Зведеним. Якщо хоча б один із […]...
- Найбільший спільний дільник (нсд) Математика – Алгебра Подільність натуральних чисел Найбільший спільний дільник (нсд) Найбільше натуральне число, на яке ділиться кожне з чисел a і b, називається найбільшим спільним дільником чисел a і b і позначається НСД (a; b). НСД можна шукати для будь-якої кількості чисел. Для знаходження найбільшого спільного дільника кількох натуральних чисел треба розкласти ці числа на […]...
- Зміни послідовності нуклеотидів ДНК МЕДИЧНА БІОЛОГІЯ Розділ 1 БІОЛОГІЧНІ ОСНОВИ ЖИТТЄДІЯЛЬНОСТІ ЛЮДИНИ 1.2. Молекулярно-генетичний і клітинний рівні організації життя 1.2.3. Спадковий апарат еукаріотичних клітин і його функціонування на молекулярному рівні 1.2.3.15. Зміни послідовності Нуклеотидів ДНК Мутації гена здебільшого є наслідком зміни послідовності нуклеотидів ДНК. Структурна класифікація мутацій гена: 1) заміна одних азотних основ іншими (транспозиція); 2) зміна кількості нуклеотидних […]...
- Геометрична прогресія УРОК № 54 Тема. Геометрична прогресія Мета уроку: домогтися засвоєння учнями: означення геометричної прогресії, відповідної термінології (знаменник геометричної прогресії), її рекурентної формули та основних властивостей геометричної прогресії (включаючи характеристичну властивість). Виробити вміння: відтворювати зміст вивчених понять, а також використовувати їх для розв’язування задач, що передбачають виділення геометричної прогресії серед інших числових послідовностей, використання рекурентної формули […]...
- Властивості нескінченно малих послідовностей Математика – Алгебра Границя Властивості нескінченно малих послідовностей Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю. Послідовність називається Обмеженою, якщо існує таке число , що для всіх значень 2, … виконується нерівність . Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою послідовністю. Послідовність називається Нескінченно […]...
- Дії над натуральними числами Математика – Алгебра Натуральні числа і дії над ними Дії над натуральними числами Додавання У записі числа a і b – доданки, число с, а також вираз – сума чисел а і b. Властивості додавання 1. Переставна. Від перестановки доданків сума не змінюється: . 2. Сполучна. Щоб до суми двох чисел додати третє число, можна […]...
- МАТЕМАТИЧНИЙ СЛОВНИК МАТЕМАТИЧНИЙ СЛОВНИК Вираз числовий – запис, який містить числа, знаки дій і дужки. Геометричне тіло об’ємна геометрична фігура, яка займає певну частину простору. Дріб число, яке містить частини цілого. Знаменник дробу – число, яке показує, на скільки рівних частин поділено ціле. Класи числа трійки послідовних розрядів числа, починаючи з одиниць. Круглі числа – числа, запис […]...