Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Прийоми додавання і віднімання в межах 1000

Прийоми додавання і віднімання в межах 1000

Прийоми додавання і віднімання в межах 1000

Мета: узагальнити й систематизувати уміння виконувати прийоми додавання і віднімання – усні та письмові.

Дидактичні задачі. Актуалізувати вміння застосовувати усні прийоми додавання і віднімання в межах 1000. Перенести прийом додавання та віднімання частинами на випадки додавання і віднімання трицифрових чисел; прийом порозрядного додавання та віднімання на випадки додавання і віднімання трицифрових чисел, а також на випадки обчислення більш, ніж двох доданків. Перенести прийом округлення на випадки додавання

і віднімання трицифрових чисел. Актуалізувати прийом письмового додавання і віднімання; перенести прийом письмового додавання на додавання у випадку трьох і більше доданків. Актуалізувати вміння розв’язувати складені задачі на знаходження суми, різницеве порівняння двох добутків.

Розвивальна задача: розвивати логічне мислення учнів (№8; РЗ ч. 1 с. 5, №3).

ХІД УРОКУ

І. МОТИВАЦІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Сьогодні на уроці ми пригадаємо відомі прийоми додавання та віднімання круглих трицифрових чисел, узагальнимо їх для інших випадків обчислення. Кожен зможе визначитись із

зручним для себе способом міркування. А для чого нам потрібно вміти знаходити значення виразів різними способами? Щоб впевнитися в тому, що знайдений результат є правильним. Навіщо це потрібно? Передусім, якщо ви самі знайдете помилку, то зможете її вчасно виправити. Це дуже важливо для майбутнього. Дорослі люди мають не лише знаходити вихід з ситуації, а й оцінювати правильність своїх дій. Сьогодні на прикладі математичних завдань ви потренуєтесь перевіряти себе. Отже, готуємось до майбутнього успішного дорослого життя! І в цьому нам передусім допоможуть заняття математикою!

ІІ. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ВИВЧЕНОГО

1.Усне опитування.

Назвіть взаємообернені арифметичні дії. ( Додавання і віднімання; множення та ділення.) Як пов’язані дії додавання і віднімання? Множення та ділення? Якою дією перевіряється дія додавання; віднімання; множення; ділення? Як перевірити правильність виконання арифметичної дії додавання; віднімання; множення; ділення? Наведіть приклади. Що означає число збільшити на кілька одиниць ( у кілька разів)? Що означає зменшити число на кілька одиниць ( у кілька разів)? Як дізнатися на скільки одиниць ( у скільки разів) одне число більше або менше за інше? Як зміниться значення суми (добутку), якщо один з доданків (множник) збільшиться на (у) кілька одиниць (разів), а інший лишиться таким самим? Наведіть приклади. Як зміниться значення різниці (частки), якщо зменшуване; від’ємник (ділене; дільник) збільшиться на (у) кілька одиниць (разів)? Наведіть приклади. Чи істинним є твердження: значення загальної величини і величини одиниці виміру ( кількості або часу) змінюються в одному напрямі – якщо одне з збільшиться (зменшиться), то й інше, так само, збільшиться (зменшиться). Сформулюйте правило додавання (віднімання) суми до (від) числа; правило додавання (віднімання) числа до (від) суми.

2.Актуалізація прийомів додавання й віднімання круглих трицифрових чисел.

Завдання №1 виконується колективно.

530 + 280 ( 740 – 570).

Перша рівність – розв’язання з використанням прийому додавання (віднімання) частинами. Цей прийом грунтується на правилі додавання (віднімання) суми до (від) числа. Пригадуємо правило. З’ясовуємо, що другий доданок ( від’ємник) при обчисленні частинами можна замінювати і сумою розрядних доданків і сумою зручних доданків. Таким чином, додавання (віднімання) частинами можна здійснити двома способами. Пропонуємо учням виконати обчислення іншим способом.

Друга рівність – додавання (віднімання) на підставі правила додавання (віднімання) числа до (від) суми. Пригадуємо правило. З’ясовуємо, що перший доданок (зменшуване) можна подати у вигляді і суми розрядних, і суми зручних доданків. Таким чином, використовуючи даний прийом можна виконати обчислення двома способами. Пропонуємо учням виконати обчислення іншим способом.

Третя рівність – реалізація прийому порозрядного додавання ( віднімання). З’ясовуємо, що при додаванні обидва доданки подаємо у вигляді суми розрядних доданків, а при відніманні, якщо є перехід через розряд, – зменшуване подаємо у вигляді суми зручних доданків, де переший доданок сотні, але на одну сотню менше, а другий – 1 сотня + десятки зменшуваного, а від’ємник подаємо у вигляді суми розрядних доданків. І при порозрядному додаванні і при порозрядному відніманні окремо виконуємо дії з сотнями, а потім з десятками; і нарешті додаємо одержані результати. Отже, при відніманні слід перевіряти, чи можна з одиниць певного розряду зменшуваного відняти одиниці цього розряду від’ємника.

Четверта рівність – додавання ( віднімання) шляхом округлення. Визначаємо, що основою цього прийому обчислення є залежність значення суми (різниці) від зміни одного з доданків ( від’ємника). Формулюємо залежність. Звертаємо увагу учнів на те, що цей спосіб міркування застосовується не для всіх випадків обчислення, а лише, тоді, коли цифра десятків одного з доданків ( від’ємника) 5 або більше.

П’ята рівність – реалізація прийому укрупнення розрядних одиниць. Теоретична основа – питання нумерації трицифрових чисел: 10 одиниць становлять 1 десяток. Замінюємо обидва числа однаковими більшими розрядними одиницями. Виконуємо додавання (віднімання) чисел десятків. Результат подаємо у одиницях.

Завдання №1 із робочого зошита виконується з коментарем.

3.Узагальнення приймів додавання та віднімання; перенесення на складніші випадки обчислення.

Завдання №2 виконується колективно.

Учні обчислюють значення першого виразу по частинах, замінюючи від’ємник (другий доданок) сумою розрядних доданків. Зіставляють другий вираз з першим: змінилося зменшуване (перший доданок), до нього дописали ліворуч ще одну цифру – одержали трицифрове число. Але на процес обчислення це, практично, не вплине, оскільки від’ємник ( другий доданок), які ми маємо замінювати сумою розрядних доданків, не змінився – до результату першого виразу треба ліворуч приписати цифру сотень. Зіставляють третій і другий вираз: змінився від’ємник (другий доданок): до нього приписали ліворуч ще одну цифру і одержали трицифрове число. Щоб відняти (додати) трицифрове число частинами, треба замінити його сумою, наприклад розрядних доданків, і по черзі відняти сотні, десятки та одиниці. Отже трицифрові числа додають і віднімають частинами аналогічно відповідним обчисленням з двоцифровими числами.

Завдання №4 виконується колективно.

Учні обчислюють значення першого виразу у стовпчику порозрядно. Зіставляють другий і перший вираз: з’ясовують, що змінилися обидва числа – до кожного з них ліворуч дописали ще одну цифру й одержали трицифрові числа. Таким чином, замінюючи трицифрові числа сумою, одержимо суми трьох доданків, а обчислюючи треба виконувати окремо дії з сотнями, дії з десятками та дії з одиницями. Трицифрові числа додають і віднімають порозрядно аналогічно відповідним обчисленням з двоцифровими числами.

Завдання №5 виконується колективно.

Учні знаходять значення першої суми порозрядно. Зіставляють другу та першу суми: друга сума містить не два, а три доданки. З’ясовують, як зміна кількості доданків вплине на розв’язування: в цьому випадку треба кожний з трьох доданків подати у вигляді суми розрядних доданків, а потім, так само, виконати окремо дії з десятками, окремо з одиницями, а потім додати одержані суми. Зіставляємо третю суму та другу і визначають, що так само можна міркувати й при порозрядному додаванні чотирьох доданків. Зауважуємо, що у такий спосіб можна лише додавати кілька доданків!

Завдання №6 виконується колективно.

Працюємо аналогічно до завдання №2. Зазначимо, що другий доданок 28 у перших двох виразах першого стовпчика замінюємо близьким круглим числом 30; а у третьому – 130. Висновок: трицифрове число, якщо воно закінчується цифрою 5; 6; 7; 8; 9, можна замінити близьким круглим числом, і додати (відняти) це число, попередньо визначивши на скільки більше додали (відняли), тому від ( до) одержаного результату відняти (додати) це число.

Завдання №7 виконується колективно.

Учні пояснюють письмовий прийом додавання та віднімання за поданими розв’язаннями. Зіставляють першу та другу суму: добавився ще один доданок. З’ясовуємо, чи можна при додаванні трьох доданків міркувати так само, як і при додаванні двох доданків. Так, можна! Учні пояснюють розв’язання. Зауважуємо, що у такий спосіб можна лише виконувати додавання трьох доданків; віднімати три доданки стовпчиком не можна, оскільки при відніманні існує потреба позичати в зменшуваному одиницю вищого розряду та роздробляти її у нижчу… і у випадку двох від’ємників легко припуститися помилки!

Решту завдань учні виконують з коментарем.

Завдання №2 із робочого зошита виконуються з коментарем.

4.Розвиток варіативного мислення учнів.

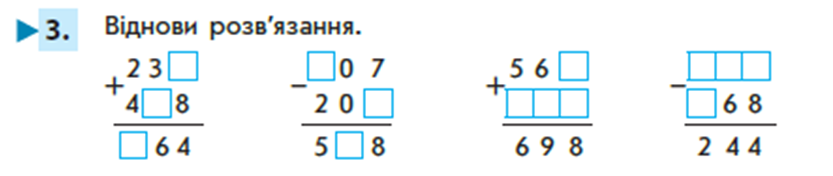
Завдання №3 із робочого зошита виконується з коментарем. Пропонуємо для третього та четвертого стовпчиків один з варіантів розв’язань.

9

1

4

1

2

1

3

0

8

8

9

6

2

6

Прийоми додавання і віднімання в межах 1000

5.Розвиток логічного мислення учнів.

Завдання №8 виконується колективно.

У Тані було 5 горіхів. Покажемо це. Не відомо, скільки горіхів було спочатку у братика. Коли Таня віддала один горіх, то в неї залишилося 4 горіхи, і в них стало горіхів порівну. Значить в неї і в брата стало по 4 горіха.

Прийоми додавання і віднімання в межах 1000

Прийоми додавання і віднімання в межах 1000

Прийоми додавання і віднімання в межах 1000

Прийоми додавання і віднімання в межах 1000

Прийоми додавання і віднімання в межах 1000Т.

Прийоми додавання і віднімання в межах 1000

Прийоми додавання і віднімання в межах 1000

Прийоми додавання і віднімання в межах 1000

Бр.

Значить, спочатку у брата було на 1 горіх менше, тобто 4 – 1 = 3 горіха.

Відповідь: у брата було 3 горіха.

Продовжимо цю задачу: Таня віддала брату 2 горіхи, тоді. Горіхів в них стало порівну…

Після розв’язання цієї задачі можна зробити висновок: якщо в двох коробках спочатку предметів не порівну, а після перекладання з першої коробки в другу кількох предметів стає в цих коробках порівну, то в першій коробці предметів більше на подвійну кількість предметів, що переклали.

УІІ. ПОЯСНЕННЯ ЗАВДАННЯ ДЛЯ ДОМАШНЬОЇ РОБОТИ

Завдання №6 – виконати додавання та віднімання трицифрових чисел письмово. Завдання № 7 – записати задачу коротко в формі таблиці, скласти план розв’язування задачі та розв’язати її; з метою перевірки правильності розв’язку скласти і розв’язати хоча б одну обернену задачу.

УІІ. ПІДСУМОК. РЕФЛЕКСІЯ НАВЧАЛЬНО-ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ

Які прийоми обчислень ми використали у складніших випадках обчислення з трицифровими числами? Як можна міркувати при додаванні та відніманні трицифрових чисел? Як можна міркувати при додаванні трьох і більше доданків, використовуючи усний прийом? Письмовий прийом? Розкажіть про результати власних навчальних досягнень: Я знаю… Я розумію… Я можу пояснити… Я вмію… Я перевіряю… Я оцінюю… Мені цікаво… В мене добре виходить… Мені ще слід попрацювати над…


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Прийоми усного множення і ділення в межах 1000 Мета: узагальнити й систематизувати уміння виконувати прийоми усного позатабличного множення та ділення. Дидактичні задачі. Актуалізувати уміння виконувати прийоми усного множення і ділення в межах 1000: множення та ділення на одноцифрове число; множення та ділення круглих чисел на одноцифрове способом укрупнення розрядних одиниць, способом множення ( ділення) добутку на число ; ділення на кругле число способом […]...

  2. Прийоми додавання і віднімання в межах 1 000 Прийоми додавання і віднімання в межах 1 000 Письмове додавання у випадку трьох доданків 1 Прокоментуй розв’язання учнів. Які прийоми обчислення вони застосували? 2 Згадай суть прийому додавання і віднімання чисел частинами. У кожному стовпчику зістав вирази. Знайди значення першого виразу частинами. Чи допоможе обчислення першого виразу знайти значення другого виразу у стовпчику? Чи можна […]...

  3. Письмове додавання і віднімання багатоцифрових чисел Мета: формувати навички письмового додавання та віднімання багатоцифрових чисел Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати способи міркування при усному додаванні та відніманні: додавання (віднімання) способом укрупнення розрядних одиниць, додавання (віднімання) частинами на підставі правила додавання (віднімання) сумі до (від) числа; додавання (віднімання) на підставі правила додавання (віднімання) числа до (від) суми; порозрядне додавання ( […]...

  4. СПОСОБИ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. ПОРІВНЯННЯ ВИРАЗУ І ЧИСЛА ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 1-Й КЛАС Урок 7. СПОСОБИ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. ПОРІВНЯННЯ ВИРАЗУ І ЧИСЛА Мета: повторити способи додавання і віднімання двоцифрових чисел; формувати вміння порівнювати вирази і числа; розвивати логічне мислення; формувати потребу розв’язувати поставлені завдання швидко і правильно. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ Пролунав уже дзвінок, Всіх покликав на урок. Тому […]...

  5. ЗВ’ЯЗОК ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ. СКЛАДАННЯ ПРИКЛАДІВ НА ВІДНІМАННЯ ІЗ ПРИКЛАДІВ НА ДОДАВАННЯ. ПРАВИЛО ЗНАХОДЖЕННЯ НЕВІДОМОГО ДОДАНКА. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 44. ЗВ’ЯЗОК ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ. СКЛАДАННЯ ПРИКЛАДІВ НА ВІДНІМАННЯ ІЗ ПРИКЛАДІВ НА ДОДАВАННЯ. ПРАВИЛО ЗНАХОДЖЕННЯ НЕВІДОМОГО ДОДАНКА. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР Мета: розкрити взаємозв’язок між додаванням і відніманням; ознайомити учнів з правилом знаходження невідомого доданка; вчити складати приклади на віднімання із […]...

  6. ВЛАСТИВОСТІ ДІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ ВЛАСТИВОСТІ ДІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ A + b = b + a A + (b + c) = (a + b) + c = a + b + c Додавання числа до суми Додавання суми до числа Віднімання числа від суми Віднімання суми від числа (a – b) + c = (a + c) – […]...

  7. ЗВ’ЯЗОК ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ. ПЕРЕВІРКА ДОДАВАННЯ ВІДНІМАННЯМ Мета: ознайомити учнів з використанням зв’язку між діями додавання і віднімання для перевірки додавання; вдосконалювати обчислювальні навички, вміння розв’язувати задачі на дві дії; розвивати логічне мислення; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Гра “Склади букет” На дошці прикріплена ваза та квіти з написаними […]...

  8. УТВОРЕННЯ, ЧИТАННЯ ТА ЗАПИСУВАННЯ П’ЯТИЦИФРОВИХ ЧИСЕЛ У МЕЖАХ 20 000. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ТРИЦИФРОВИХ ЧИСЕЛ. НЕРІВНОСТІ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ОЗНАЙОМИТИ З УТВОРЕННЯМ, ЧИТАННЯМ ТА ЗАПИСОМ П’ЯТИЦИФРОВИХ ЧИСЕЛ У МЕЖАХ 20 000; ПОВТОРИТИ ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ТРИЦИФРОВИХ ЧИСЕЛ; ФОРМУВАТИ ВМІННЯ ЗНАХОДИТИ ЗНАЧЕННЯ НЕВІДОМИХ У НЕРІВНОСТЯХ; УДОСКОНАЛЮВАТИ ВМІННЯ ПОРІВНЮВАТИ ЗАДАЧІ I. Перевірка домашнього завдання Взаємоперевірка учнями виконаних завдань один у одного в парах. II. Актуалізація та корекція опорних знань учнів 1. Завдання […]...

  9. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 1. ОБЧИСЛЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ. ДОДАВАННЯ І ВІДНІМАННЯ ПО 1 ВИДУ 4 + 1 + 1; 9 ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 50. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 1. ОБЧИСЛЕННЯ ЗНАЧЕНЬ ВИРАЗІВ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ. ДОДАВАННЯ І ВІДНІМАННЯ ПО 1 ВИДУ 4 + 1 + 1; 9 – 1 – 1 Мета: на основі практичних вправ і знань про послідовність чисел у натуральному ряді розкрити прийоми додавання і віднімання […]...

  10. Письмове додавання й віднімання чисел у межах 1000 Розділ 3. Письмове додавання й віднімання чисел у межах 1000 410. 460 – 240 = 220 270 – (50 + 70) = 270 – 120 = 150 340 + 24 = 364 81 : 9 + 340 = 9 + 340 = 349 830 + 100 = 930 270 + 40 = 310 412. 413. […]...

  11. Додавання і віднімання багатоцифрових чисел Мета: формувати обчислювальні навички Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати розуміння залежності значення суми від зміни одного з доданків, залежності значення різниці від зміни від’ємника. Актуалізувати прийом округлення при додаванні і відніманні; застосування прийому округлення до випадків додавання і віднімання, чисел, близькі до розрядних одиниць: 99,999,9999… . Формувати навички додавання та віднімання багатоцифрових чисел […]...

  12. Арифметичні дії додавання і віднімання Метою розділу є формування в учнів навичок письмового додавання та віднімання багатоцифрових чисел. Слід зазначити, що з письмовим прийомами додавання та віднімання учні ознайомились у 3-му класі, на початку навчального року в 4-му класі алгоритми письмових прийомів були актуалізовані, водночас розглядалось письмове додавання у випадку трьох доданків. Таким чином, тривалий час було відведено для формування […]...

  13. УСНЕ ДОДАВАННЯ І ВІДНІМАННЯ У МЕЖАХ 100 З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ ТА ДІЛЕННЯ (продовження) Урок 134. УСНЕ ДОДАВАННЯ І ВІДНІМАННЯ У МЕЖАХ 100 З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД Мета: повторити усне додавання і віднімання у межах 100 з переходом через розряд; удосконалити вміння розв’язувати прості і складені задачі; розвивати увагу, навички самоконтролю; виховувати працьовитість Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. […]...

  14. Додавання і віднімання в межах 1000 Додавання і віднімання в межах 1000 480. Розв’язання: 1) 1000 – 700 = 300 (г) – міді; 2) 700 – 300 = 400 (г) Відповідь: на 400 грамів більше срібла. 485. Розв’язання: 1) 16 : 8 = 2 (м) – на І верстаті за 1 год; 2) 2 + 2 = 4 (м) – на […]...

  15. НУМЕРАЦІЯ ЧИСЕЛ 1-100. ВИПАДКИ ДОДАВАННЯ І ВІДНІМАННЯ В МЕЖАХ 100, ПОВ’ЯЗАНІ З НУМЕРАЦІЄЮ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ПРОСТИХ ЗАДАЧ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 1-Й КЛАС Урок 1. НУМЕРАЦІЯ ЧИСЕЛ 1-100. ВИПАДКИ ДОДАВАННЯ І ВІДНІМАННЯ В МЕЖАХ 100, ПОВ’ЯЗАНІ З НУМЕРАЦІЄЮ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ПРОСТИХ ЗАДАЧ Мета: повторити нумерацію чисел 1-100; вдосконалити обчислювальні навички, вміння розв’язувати прості задачі; розвивати кмітливість, мислення учнів; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Ознайомлення […]...

  16. Додавання і віднімання багатоцифрових чисел на основі нумерації Мета: формувати уявлення про багатоцифрові числа. Дидактичні задачі. Актуалізувати знання послідовності чисел в натуральному ряді в заданих межах; способу порівняння чисел на підставі їх прямування в натуральному ряді; вміння читати багатоцифрові числа, визначати їх розрядний склад; записувати багатоцифрові числа і порівнювати їх. Актуалізувати вміння замінювати суму розрядних доданків багатоцифровим числом; розуміння взаємозв’язку додавання і віднімання; […]...

  17. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 2. ДОДАВАННЯ І ВІДНІМАННЯ ВИДУ 7 + 2 + 1; 8 – 2 ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 52. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 2. ДОДАВАННЯ І ВІДНІМАННЯ ВИДУ 7 + 2 + 1; 8 – 2 – 2. ДОДАВАННЯ І ВІДНІМАННЯ ПО 2. РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: ознайомити учнів з таблицями додавання і віднімання числа 2; вправляти у розв’язуванні прикладів виду 7 + 2 […]...

  18. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 4. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА ЧАСТИНАМИ ВИДУ 5 + 2 + 2; 5 – 2 ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 60. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 4. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА ЧАСТИНАМИ ВИДУ 5 + 2 + 2; 5 – 2 – 2. СКЛАДАННЯ І РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: ознайомити учнів з таблицями додавання і віднімання числа 4; вчити додавати і віднімати числа частинами виду 5 + […]...

  19. ЧИСЛОВІ МНОЖИНИ. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: повторити усну і письмову нумерацію чисел першої сотні; випадки додавання і віднімання в межах 20; розвивати мислення, пам’ять; виховувати акуратність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання (с. 153, завдання 984; 985) Завдання 984 Стає був у таборі з 15 липня по 7 серпня включно. Скільки днів був […]...

  20. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 3. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА ЧАСТИНАМИ ВИДУ 6 + 2 + 1; 9 ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 56. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 3. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА ЧАСТИНАМИ ВИДУ 6 + 2 + 1; 9 – 2 – 1. ДОДАВАННЯ І ВІДНІМАННЯ ПО 3. РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: формувати в учнів уміння складати таблиці додавання і віднімання числа 3; продовжити роботу над складанням […]...

  21. Арифметичні дії додавання і віднімання, множенняі ділення Мета: узагальнити й систематизувати навчальний досвід учнів відносно сутності арифметичних дій додавання й віднімання, множення та ділення, законів та властивостей арифметичних дій. Дидактичні задачі. Актуалізувати поняття про арифметичні дії закони і властивості арифметичних дій та їх застосування для полегшення обчислень ; Наголосити на теоретичній основі усних прийомів обчислення. Актуалізувати уміння застосовувати прийоми усного додавання, віднімання, […]...

  22. Прийоми усного множення і ділення в межах 1000 Прийоми усного множення і ділення в межах 1000 – Укрупнення розрядних одиниць – Послідовне множення; ділення 1 Перевір і прокоментуй розв’язання учнів. Які прийоми обчислення застосовано? Зістав випадки множення; випадки ділення. Чим вони відрізняються? Як ця відмінність впливає на розв’язання? 56 ∙ 6 = (50 + 6) ∙ 6 = 50 ∙ 6 + 6 […]...

  23. ОКРУГЛЕННЯ ЧИСЕЛ. ПРИЙОМИ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 3 КЛАС ОКРУГЛЕННЯ ЧИСЕЛ. ПРИЙОМИ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 30. Випиши спочатку розрядні числа, потім круглі. Прочитай числа, які не є круглими. Чи всі розрядні числа є круглими? 700 320 500 784 30 640 300 325 400 115 31. У господаря 189 кущів винограду. Що точніше: у господаря приблизно 1 сотня чи […]...

  24. ТАБЛИЦЯ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ПЛАНОМ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ЗАДАЧІ НА ДВІ ДІЇ Урок 25. ТАБЛИЦЯ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ПЛАНОМ Мета: узагальнити знання таблиць додавання і віднімання чисел; формувати вміння розв’язувати задачі за планом; виховувати пізнавальний інтерес до вивчення математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ […]...

  25. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 5. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА ЧАСТИНАМИ ВИДУ 3 + 2 + 3; 6 – 2 ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 63. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 5. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА ЧАСТИНАМИ ВИДУ 3 + 2 + 3; 6 – 2 – 3. ЗБІЛЬШЕННЯ І ЗМЕНШЕННЯ ЧИСЕЛ НА 5. СКЛАДАННЯ І РОЗВ’ЯЗУВАННЯ ЗАДАЧІ ЗА МАЛЮНКОМ. ПОБУДОВА ВІДРІЗКІВ Мета: ознайомити учнів з таблицями додавання й віднімання числа […]...

  26. Додавання і віднімання іменованих чисел Мета: формувати обчислювальні навички. Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати прийоми письмового додавання та віднімання, способи перевірки одержаних результатів; способи заміни складеного іменованого числа простим, простого іменованого числа – складеним; письмовий прийом додавання і віднімання простих іменованих чисел. Створити та розв’язати проблемну ситуації, у наслідок якої відбудеться відкриття двох способів міркування при додаванні і […]...

  27. НАЗВИ КОМПОНЕНТІВ ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ. ЗАДАЧІ НА РІЗНИЦЕВЕ ПОРІВНЯННЯ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 1-Й КЛАС Урок 3. НАЗВИ КОМПОНЕНТІВ ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ. ЗАДАЧІ НА РІЗНИЦЕВЕ ПОРІВНЯННЯ Мета: повторити назви компонентів дій додавання і віднімання, таблиці додавання і віднімання; формувати вміння розв’язувати задачі на різницеве порівняння; виховувати уважність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання (с. 6, завдання 20; […]...

  28. ДОДАВАННЯ І ВІДНІМАННЯ ПО 4. ЗНАХОДЖЕННЯ НЕВІДОМИХ КОМПОНЕНТІВ ДІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ. РОЗВ’ЯЗУВАННЯ І ПОРІВНЯННЯ ЗАДАЧ. ПОБУДОВА ВІДРІЗКІВ ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 61. ДОДАВАННЯ І ВІДНІМАННЯ ПО 4. ЗНАХОДЖЕННЯ НЕВІДОМИХ КОМПОНЕНТІВ ДІЙ ДОДАВАННЯ ТА ВІДНІМАННЯ. РОЗВ’ЯЗУВАННЯ І ПОРІВНЯННЯ ЗАДАЧ. ПОБУДОВА ВІДРІЗКІВ Мета: вправляти учнів у засвоєнні табличних випадків додавання і віднімання числа 4, додаванні і відніманні по 4, знаходженні невідомих компонентів дій додавання та віднімання; вчити розв’язувати і […]...

  29. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 7 З ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК. СКЛАДАННЯ Й РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА СХЕМАТИЧНИМ ЗАПИСОМ ЇХ УМОВИ. ЗНАХОДЖЕННЯ НЕВІДОМОГО ДОДАНКА ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ Урок 17. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 7 З ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК. СКЛАДАННЯ Й РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА СХЕМАТИЧНИМ ЗАПИСОМ ЇХ УМОВИ. ЗНАХОДЖЕННЯ НЕВІДОМОГО ДОДАНКА Мета: ознайомити учнів з таблицями додавання і віднімання числа 7 з переходом через десяток; […]...

  30. Віднімання раціональних чисел. Властивості віднімання Урок № 7 4 Тема. Віднімання раціональних чисел. Властивості віднімання Мета: доповнити уявлення учнів властивостями віднімання; відпрацювати навички замінювати віднімання додаванням і знаходити значення утворених сум. Тип уроку: застосування знань, навичок та вмінь. Хід уроку І. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Закінчіть речення: “Щоб від числа [а] відняти число 7 [-6], […]...

  31. ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 20 З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД Розділ 2. ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 20 З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД 118. Гра “Хто швидше долетить до Місяця?”. Якщо отримали однакову відповідь, то обрали правильний шлях. Рухайтеся від зірки до зірки. 119. Кожне з чисел доповни до 10 120. Розглянь, як виконали додавання і віднімання 121. Розв’яжи пряму і обернену задачі. – […]...

  32. ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ БЕЗ ПЕРЕХОДУ ЧЕРЕЗ ДЕСЯТОК. ПЕРИМЕТР ТРИКУТНИКА Мета: повторити прийоми додавання і віднімання двоцифрових чисел без переходу через десяток; формувати обчислювальні навички; розвивати вміння обчислювати периметр трикутника, розв’язувати задачі; виховувати уважність. Хід уроку І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання 2. Математичний диктант – Запишіть число, в якому 6 десятків і 5 одиниць; 2 десятки і 8 одиниць. […]...

  33. УСНЕ ДОДАВАННЯ І ВІДНІМАННЯ ВИДУ 430 + 500; 430 + 50; 760 Мета: формувати в учнів уміння застосовувати загальні правила додавання і віднімання трицифрових чисел до окремих випадків, коли в одному із компонентів цих дій відсутні сотні або десятки; закріплювати вміння розв’язувати задачі; розвивати мислення; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ (див. додаток на с. 147) III. ПОВІДОМЛЕННЯ ТЕМИ УРОКУ […]...

  34. ЗАКРІПЛЕННЯ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. САМОСТІЙНА РОБОТА УСНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 100 З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД Урок 48. ЗАКРІПЛЕННЯ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. САМОСТІЙНА РОБОТА Мета: удосконалити навички додавання і віднімання двоцифрових чисел; закріпити вміння розв’язувати задачі на дві дії; розвивати математичне мовлення; виховувати інтерес до математики, самостійність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. […]...

  35. Письмове додавання й віднімання трицифрових чисел. Знаходження значень буквених виразів. Задачі на 3 дії УРОК 3 Тема. Письмове додавання й віднімання трицифрових чисел. Знаходження значень буквених виразів. Задачі на 3 дії Мета: повторити алгоритм письмового додавання й віднімання чисел; опрацювати розширену задачу на знаходження третього доданка; ознайомити учнів з розміщенням відрізків на площині і в просторі. Обладнання: предметні малюнки, таблиця “Додавання й віднімання трицифрових чисел”. ХІД УРОКУ I. Контроль […]...

  36. Величини. Метрична система мір. Додавання й віднімання багатоцифрових чисел УРОК 130 Тема. Величини. Метрична система мір. Додавання й віднімання багатоцифрових чисел Мета: узагальнити й систематизувати знання учнів про дії додавання й віднімання багатоцифрових чисел, їх закони; вдосконалювати навички усної лічби. ХІД УРОКУ I. Контроль і закріплення знань учнів Усні обчислення – Обчислити зручним способом. 130 + 250 + 170 + 250 147 – (47 […]...

  37. ДІЯ ДОДАВАННЯ. ЗАКОНИ ДОДАВАННЯ. ТАБЛИЧНЕ Й ПОЗАТАБЛИЧНЕ, УСНЕ І ПИСЬМОВЕ ДОДАВАННЯ. ЗАДАЧІ, ЯКІ РОЗВ’ЯЗУЮТЬСЯ ДОДАВАННЯМ Мета: узагальнити уявлення учнів про дію додавання та її закони; закріпити вміння розв’язувати задачі на додавання; повторити прийоми письмового додавання трицифрових чисел; розвивати уважність; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення Гра “Ланцюжок” Зменшуване 400, від’ємник 120, знайди різницю; до […]...

  38. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ БАГАТОЦИФРОВИХ ЧИСЕЛ. ЗАДАЧІ, ЯКІ РОЗВ’ЯЗУЮТЬСЯ ВІДНІМАННЯМ Мета: ознайомити учнів з прийомом письмового додавання і віднімання багатоцифрових чисел у межах мільйона; вдосконалювати вміння розв’язувати рівняння, задачі; розвивати мислення, математичну пильність; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення. Робота в парах – Додайте відповіді в порядку спадання – […]...

  39. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 4 З ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК. ВИМІРЮВАННЯ ДОВЖИНИ ЛАМАНОЇ ЛІНІЇ. ЗАДАЧІ НА ЗНАХОДЖЕННЯ СУМИ ТА ОСТАЧІ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ Урок 12. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 4 З ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК. ВИМІРЮВАННЯ ДОВЖИНИ ЛАМАНОЇ ЛІНІЇ. ЗАДАЧІ НА ЗНАХОДЖЕННЯ СУМИ ТА ОСТАЧІ Мета: ознайомити учнів з таблицями додавання і віднімання числа 4 з переходом через десяток; розвивати вміння […]...

  40. Додавання на основі розрядного складу числа Додавання на основі розрядного складу числа Сума розрядних доданків 1 Назви числа: більші за 5 489, але менші від 5 512; більші за 34 987, але менші від 35 020; більші за 267 178, але менші від 267 207. 2 Запиши числа. Розбий отриману множину на підмножини. Прочитай елементи кожної підмножини. Допиши до кожної підмножини […]...

Ви зараз читаєте: Прийоми додавання і віднімання в межах 1000
«
»