Промінь, пряма, площина
Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ
§ 17. Промінь, пряма, площина
Продовжимо відрізок АВ за допомогою лінійки за точку В (рис. 38). На рисунку таке продовження обмежене розмірами аркуша, але можна уявити, що ми продовжили відрізок необмежено. Якщо продовжити відрізок АВ за його кінець В необмежено, то одержимо промінь АВ. Точка А – початок променя АВ. Кінця у променя немає. При позначенні променя на першому місці пишуть букву, яка означає початок променя.

Рис. 38
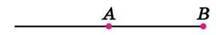
Рис. 39
Якщо продовжити відрізок АВ за його кінець А, то дістанемо промінь ВА (рис. 39). Його початок – точка В.
Якщо продовжити відрізок АВ за обидва кінці необмежено (рис. 40), то дістанемо фігуру, що має назву пряма. Пряма не має початку і кінця. Пряму, як і відрізок, позначають двома великими буквами, які позначають будь-які дві точки, що лежать на цій прямій. Наприклад, на рисунку 40 зображено пряму АВ, або ВА. Пряму АВ можна також позначити однією малою буквою латинського алфавіту, наприклад пряма а. Про точки А і В будемо говорити, що вони належать прямій а (або АВ).

Рис.
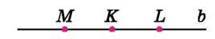
Рис. 41
Через будь-які дві точки можна провести пряму і до того ж тільки одну.
Кожна точка, яка належить прямій, розбиває її на два промені. На рисунку 41 точка К розбиває пряму b на промені КМ і KL. Ці промені є частиною прямої і мають єдину спільну точку К – початок цих променів. Такі промені називаються доповняльними (один з них доповнює інший до прямої).
Точка, відрізок, промінь, пряма – геометричні фігури. Ці геометричні фігури можна розмістити на площині (рис. 42). Площина є однією з основних геометричних фігур. Уявлення про частину площини дає, наприклад, поверхня стола, шибки, стелі, якщо уявити, що вони необмежено продовжені. Коли креслимо фігури, то частиною площини може бути, наприклад, аркуш зошита або шкільна дошка.
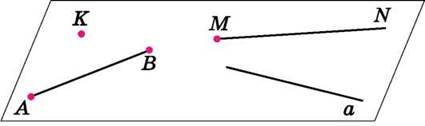
Рис. 42
588. Накресли пряму, познач на ній три точки. Виміряй довжини всіх утворених відрізків.
589. Розглянь рисунок 48. Чи правильні такі твердження:
1) точка D належить відрізку АС;
2) точка D належить променю АС;
3) точка С лежить між точками В і D;
4) точка D належить прямій АВ;
5) промені ВА і CD – доповняльні;
6) точка В належить і променю АС, і променю СА?

Рис. 48
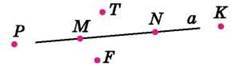
Рис. 49
590. Які з точок, зображених на рисунку 49, належать прямій а, а які – не належать?
591. Накресли промінь з початком у точці А і познач на ньому будь-яку точку В. Відклади на промені відрізок АK = 5 см та виміряй відрізок ВK.
592. Чи перетинаються (рис. 50):
1) пряма АВ і відрізок CD;
2) пряма АВ і промінь CD;
3) пряма АВ і промінь DC;
4) прямі АВ і CD;
5) промені АВ і ТО;
6) промені АВ і ОТ?
593. На скільки частин ділять площину дві прямі, які перетинаються?
594. На скільки частин ділять площину дві прямі, які не перетинаються?
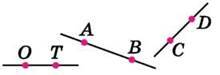
Рис. 50
Достатній рівень
595. Познач у зошиті три точки А, В і C, які не лежать на одній прямій. Проведи всі прямі, кожна з яких проходить через дві точки. Скільки є таких прямих?
596. Накресли два промені так, щоб їх спільною частиною були: 1) точка; 2) відрізок.
597. Накресли два промені з початком в одній і тій самій точці A. На скільки частин поділять площину ці промені?
598. Накресли промінь АВ. Побудуй доповняльний промінь до АВ. На кожному промені від його початку відклади відрізок, який дорівнює 4 см 5 мм. Яка відстань між двома крайніми точками на рисунку?
Високий рівень
599. Накресли пряму CD, промінь МК і відрізок АВ так, щоб пряма CD перетинала промінь МК і відрізок АВ, а промінь МК не перетинався з відрізком АВ.
600. Накресли пряму CK, промінь AE і відрізок MN так, щоб пряма CK перетинала відрізок MN і не перетинала промінь AE, а промінь AE перетинав відрізок MN.
601. На прямій позначено точки А, В і C. Причому АВ = 37 см, ВС = 42 см. Яка відстань може бути між А і C? Скільки випадків має задача?
602. Села M, N і К розташовані на прямолінійному шляху. Відомо, що MN = 7 км, MK = 13 км. Яка відстань може бути між селами N і К? Скільки випадків має задача?
Вправи для повторення
603. Обчисли значення виразу (а + а : 9) – b, якщо а = 1107, b = 978.
604. Обчисли:
1) 12 хв 37 с + 35 хв 42 с;
2) 7 хв 13 с – 5 хв 19 с;
3) 15 год 42 хв + 12 год 17 хв;
4) 4 год 15 хв – 59 хв.
605. Усі натуральні числа від 1 до 60 записано в один ряд. Скільки разів повторюється в цьому ряді цифра 5?