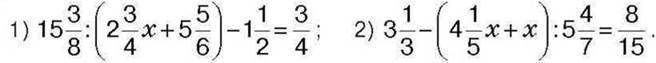Головна ⇒ 📌Математика ⇒ ПРЯМА ТА ОБЕРНЕНА ПРОПОРЦІЙНІ ЗАЛЕЖНОСТІ

ПРЯМА ТА ОБЕРНЕНА ПРОПОРЦІЙНІ ЗАЛЕЖНОСТІ

Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ

§ 14. ПРЯМА ТА ОБЕРНЕНА ПРОПОРЦІЙНІ ЗАЛЕЖНОСТІ

За допомогою пропорцій можна розв’язувати задачі.

Ви знаєте, наприклад, що вартість товару залежить від його кількості: що більшу кількість товару купують, то більшою буде його вартість. Такі величини називають прямо пропорційними.

Запамятайте!

Дві величини називаються прямо пропорційними, якщо при збільшенні (зменшенні) однієї величини в кілька разів інша величина збільшується (зменшується) в ту саму кількість разів.

Задача 1. За 2 кг цукерок

заплатили 72 грн. Скільки будуть коштувати 4,5 кг цих цукерок?

Розв’язання.

Зверніть увагу:

Якщо дві величини прямо пропорційні, то пропорцію утворюють відношення відповідних значень цих величин.

На практиці, крім прямої пропорційної залежності величин, зустрічається й обернена пропорційна залежність. Наприклад, дорогою до школи, коли часу обмаль, ви збільшуєте швидкість свого руху, щоб не запізнитися на урок. Отже, швидкість вашого руху залежить від чазу руху: що меншим е час руху, то більшою буде ваша швидкість. Такі величини називають обернено пропорційними.

Запам’ятайте!

Дві

величини називаються обернено пропорційними, якщо при збільшенні (зменшенні) однієї величини в кілька разів інша величина зменшується (збільшується) в ту саму кількість разів.

Задача 2. Автомобіль, рухаючись зі швидкістю 90 км/год, у проїхав відстань від Черкас до Києва за 2 год 3 якою швидкістю він рухався в зворотному напрямку, якщо відстань від Києва до Черкас він подолав за 2,5 год?

Розв’язання.

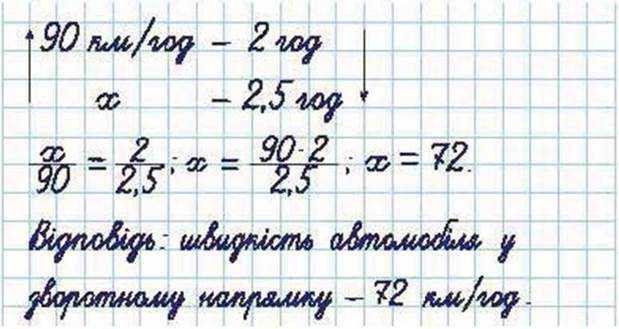
Зверніть увагу:

Якщо дві величини обернено пропорційні, то пропорцію утворюють взаємно обернені відношення відповідних значень цих величин.

? Чи завжди дві величини є прямо пропорційними або обернено пропорційними? Поміркуємо. Наприклад, під час хвороби температура дитини може то зростати, то спадати протягом кількох днів. І тут немає залежності, а значить, не може бути й пропорційності. А от зріст дитини постійно збільшується при збільшенні її віку. Отже, є залежність між величинами, а значить, є підстави аналізувати, чи пропорційні дані величини. Зрозуміло, що пропорційної залежності тут немає, тому з’ясовувати, як саме пропорційні ці величини – прямо чи обернено, – не треба. Якщо ж дві величини пропорційні, то можливі лише два варіанти, які взаємно виключають один одного, – або пряма пропорційність, або обернена пропорційність.

Дізнайтеся більше

З історією золотого перерізу непрямим чином пов’язане ім’я італійського математика і ченця Леонардо з Пізи (1180-1240 pp.), більш відомого як Фібоначчі (син Боначчі).

Він багато подорожував Сходом, познайомив Європу з індійськими (арабськими) цифрами. У 1202 р. побачила світ його математична праця “Книга про абаки” (лічильні дошки), у якій були зібрані всі відомі на той час завдання. Одне із завдань було таке: “Скільки пар кроликів за один рік від однієї пари народиться?”. Розмірковуючи на цю тему, Фібоначчі вибудував такий ряд чисел:

0, 1, 1,2, 3, 5, 8, 13,21, 34,55, … .

Нині ця послідовність чисел відома як ряд Фібоначчі. Особливість цієї послідовності чисел полягає в тому, що кожен її член, починаючи з третього, дорівнює сумі двох попередніх:

0 + 1 = 1; 1+1 = 2; 1+2 = 3; 2 + 3 = 5;

3 + 5 = 8; 5 + 8=13; 8 + 13 = 21; 13 + 21=34

Тощо, а відношення сусідніх чисел ряду наближається до відношення золотого перерізу. Наприклад:

21 : 34 = 0,617, а34 : 55 = 0,618.

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Які величини називаються прямо пропорційними? Наведіть приклади.

2. Як розв’язують задачі на пряму пропорційність?

3. Які величини називаються обернено пропорційними? Наведіть приклади.

4. Я к розв’язують задачі на обернену пропорційність?

5. Чи завжди дві величини є пропорційними?

589′. Дві величини прямо пропорційні. Як зміниться одна величина, якщо іншу: а) збільшити в 5 разів; б) зменшити у 2 рази?

Відповідь поясніть.

590′. За умовою задачі склали скорочений запис:

1)3-36, 2) 70-3, 3) 2-100,

4-48; 60-2; 4-50.

Чи є дані величини прямо пропорційними?

591′. Дві величини обернено пропорційні, Як зміниться одна величина, якщо інша:

А) збільшиться в 4 рази; б) зменшиться в 6 разів?

Відповідь поясніть.

592′. За умовою задачі склали скорочений запис:

1) 80-4, 2)3-18, 3)10-8,

160 – 2; 5 – 30; 4 – 20.

Чи є дані величини обернено пропорційними?

593°. Визначте, чи є прямо пропорційною дана залежність величин:

1) вартість товару, купленого по одній ціні, і кількість товару;

2) маса коробки цукерок і кількість однакових цукерок у коробці;

3) шлях, який проїхав автомобіль зі сталою швидкістю, і час руху;

4) швидкість руху і час руху для подолання певної відстані;

5) вага людини і її зріст;

Б) маса ягід і маса цукру для приготування варення;

7) периметр прямокутника і довжина однієї з його сторін;

8) довжина сторони квадрата і його периметр.

594°. За скороченим записом задачі знайдіть х, якщо величини є прямо пропорційними.

1) 3 кг цукерок -36 грн, 2) 15 деталей – 3год,

6 кг цукерок – х; х -2 год.

595°. Скільки коштують 10 кг цукерок, якщо за 4 кг таких цукерок заплатили 128 грн?

596°. За 3 кг яблук заплатили 24 грн. Скільки коштують 7 кг таких яблук?

597°. За 4 год катер проплив 80 км. Яку відстань пропливе катер за 2 год, рухаючись із такою самою швидкістю?

598°. Турист пройшов 20 км за 5 год. За скільки годин турист подолає відстань 28 км, рухаючись із такою самою швидкістю?

599°. При випіканні хліба з 1 кг житньої муки отримують 1,4 кг хліба. Скільки потрібно муки, щоб отримати 42 ц хліба?

600°. Із 3 кг сирих зерен кави отримують 2,5 кг смажених зерен. Скільки кілограмів сирих зерен кави треба взяти, щоб отримати 10 кг смажених?

601 °. Відстань 210 км автомобіль проїхав за 3 год. Яку відстань проще автомобіль за 2 год, рухаючись із такою самою швидкістю?

602°. Безхвоста мавпа гібон, стрибаючи з дерева на дерево, за 2 год долає відстань 32 км. Яку відстань подолає гібон за 3 год?

603°. Визначте, чи є обернено пропорційною дана залежність величин:

1) ціна товару і вартість покупки;

2) маса коробки цукерок і її вартість;

3) швидкість руху і час руху для подолання певної відстані;

4) швидкість руху автомобіля і шлях, який він проїхав зі сталою швидкістю;

5) обсяг виконаної роботи і час її виконання;

6) продуктивність праці і час на її виконання для певного обсягу роботи;

7) кількість автомобілів і вантаж, який вони перевезуть за визначений час;

8) довжина сторони квадрата і його площа.

604°. За скороченим записом задачі знайдіть х, якщо величини є обернено пропорційними.

1) 3 год – 80 км/год, 2) 5 робітників -8 днів,

4 год – х; х -10 днів.

605°. Замовлення на виготовлення меблів 3 столяри виконали за 12 днів. За скільки днів зможуть виконати це замовлення 6 столярів, якщо їх продуктивність праці буде однаковою?

606°, За скільки днів виконають завдання 6 робітників, якщо 2 робітники можуть виконати це завдання за 9 днів?

607°. Червоний кенгуру рухався 3 год зі швидкістю 55 км/год. Якою має бути швидкість кенгуру, щоб цю відстань він зміг подолати за 2,5 год?

608°. Якою має бути швидкість потяга за новим розкладом, щоб проїхати відстань між двома станціями за 4 год, якщо відповідно до старого розкладу, рухаючись зі швидкістю 100 км/год, він долав її за 5 год?

609. За 4 кг печива заплатили 56 грн. Скільки будуть коштувати 3 кг цукерок, ціна яких на 2 грн більша, ніж ціна печива?

610. 5 кг яблук коштують 40 грн. Знайдіть вартість 2 кг груш, ціна яких на 4 грн більша, ніж ціна яблук.

611. Маятник настінного годинника робить 730 коливань за 15 хв. Скільки коливань він зробить за 1 год? За скільки часу маятник зробить 2190 коливань?

612. За 24 зошити Наталка заплатила 60 грн. Скільки коштують 20 таких зошитів? Скільки таких зошитів можна купити за 45 грн?

613. У бідоні 12 л молока. Його розлили порівну в 6 банок. Скільки літрів молока в кожній банці? Скільки трилітрових банок можна наповнити молоком із цього бідона?

614. Через водопровідний кран витікає за хвилину 6 л води. Скільки води витече через кран за півгодини? За який час через кран витече 27 л води?

615. Відстань між станціями становить 360 км. За який час проїде цю відстань потяг, який за годину долає 90 км? Якою має бути швидкість потяга, щоб він міг пройти цю відстань за 4 год 30 хв?

616. Відстань між селами становить 18 км. За який час проще цю відстань велосипедист, швидкість якого становить 12 км/год? З якою швидкістю треба рухатись пішоходу, щоб пройти цю відстань за 6 год?

617. Два трактори зорали поле за 6 днів. За скільки днів зорють це поле 4 трактори, якщо будуть працювати з такою самою продуктивністю праці? Скільки тракторів потрібно, щоб зорати це поле за 2 дні?

618. Вісім вантажівок можуть перевезти вантаж за 3 дні. За скільки днів зможуть перевезти вантаж 6 таких вантажівок? Скільки вантажівок потрібно, щоб перевезти цей вантаж за 2 дні?

619. Складіть і розв’яжіть задачу на:

1) пряму пропорційність, для розв’язування якої потрібно скласти пропорцію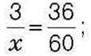

2) обернену пропорційність, для розв’язування якої потрібно скласти пропорцію х : 4 = 120 : 160.

620. Складіть і розв’яжіть задачу на: 1) пряму пропорційність, для розв’язування якої потрібно скласти пропорцію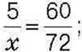

2) обернену пропорційність, для розв’язування якої потрібно скласти пропорцію 3 : х = 90 : 60.

621 *. Тарасик може пройти шлях від залізничної станції до селища за 20 хв. За який час він доїде на велосипеді від станції до селища, якщо швидкість його руху на велосипеді у 2 рази більша, ніж швидкість руху пішки?

622*. Майстер, працюючи самостійно, виконує роботу за 3 дні, а разом з учнем – за 2 дні. За скільки днів учень може виконати цю роботу самостійно?

623*. Дмитрик пробігає 4 круги по біговій доріжці за такий самий час, за який Катруся пробігає 3 круги. Катруся пробігла 12 кругів. Скільки кругів за цей час пробіг Дмитрик?

624*. Із басейну можуть викачати воду за 1 год 15хв. Через скільки часу після початку роботи в басейні залишиться 0,2 тієї кількості води, яка була спочатку?

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

625. Для друкування книги передбачалося розміщувати на кожній сторінці по 28 рядків, у кожному рядку – по 40 літер. Проте виявилося, що доцільніше розміщувати на кожній сторінці по 35 рядків. Скільки в такому випадку буде розміщуватись у кожному рядку літер під час друкування цієї книги, якщо кількість літер на сторінках не зміниться?

626. Для приготування 12 тістечок потрібно взяти білок одного яйця і 3 столові ложки цукру. Скільки цих продуктів треба взяти для приготування 24такихтістечок? Скільки таких тістечок вийде, якщо є 3 яйця?

ЗАДАЧІ НА ПОВТОРЕННЯ

627. Яке число треба вписати в останню клітинку ланцюжка?