Прямокутний трикутник
Геометрія
Основні властивості найпростіших геометричних фігур
Прямокутний трикутник
Трикутник називається Прямокутним, якщо він має прямий кут.
Сторона, яка лежить проти прямого кута, називається Гіпотенузою.
Сторони, що утворюють прямий кут, називаються Катетами.
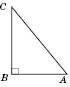
На рисунку 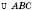 – прямокутний. AB і BC – катети, AC – гіпотенуза.
– прямокутний. AB і BC – катети, AC – гіпотенуза.
Теорема. Сума гострих кутів прямокутного трикутника дорівнює 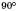 .
.
Ознаки рівності прямокутних
Теорема 1. Якщо гіпотенуза й катет одного прямокутного трикутника відповідно дорівнюють гіпотенузі й катету другого прямокутного трикутника, то такі трикутники рівні.
Теорема 2. Якщо два катети одного прямокутного трикутника відповідно дорівнюють двом катетам другого трикутника, то такі трикутники рівні.
Теорема 3. Якщо гіпотенуза й гострий кут одного прямокутного трикутника відповідно дорівнюють гіпотенузі й гострому куту другого трикутника, то такі трикутники рівні.
Теорема 4. Якщо катет і прилеглий (протилежний) гострий кут одного прямокутного трикутника відповідно дорівнюють катету
Властивість катета, протилежного куту в 30°
Теорема 1. У прямокутному трикутнику з кутом 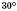 катет, протилежний цьому куту, дорівнює половині гіпотенузи.
катет, протилежний цьому куту, дорівнює половині гіпотенузи.
Теорема 2. Якщо в прямокутному трикутнику катет дорівнює половині гіпотенузи, то протилежний цьому катету кут дорівнює 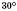 .
.
Related posts:
- ПРЯМОКУТНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 16. ПРЯМОКУТНИЙ ТРИКУТНИК Трикутник наливають прямокутним, якщо один із його кутів – прямий. Сума двох інших його кутів дорівнює 90°, бо 180° – 90° = 90°. Сторона прямокутного трикутника, що лежить проти прямого кута, – це гіпотенуза, дві інші його сторони – катети (мал. 196). На малюнку прямий кут іноді позначають […]...
- Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...
- Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...
- Властивості подібних фігур Геометрія Подібність фігур Властивості подібних фігур Теорема. Коли фігура подібна фігурі , а фігура – фігурі , то фігури і Подібні. Із властивостей перетворення подібності випливає, що у подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Наприклад, у подібних трикутниках ABC і : ; ; ; . Ознаки подібності трикутників Теорема 1. Якщо два […]...
- Співвідношення між сторонами й кутом прямокутного трикутника Геометрія Трикутники Співвідношення між сторонами й кутом прямокутного трикутника Нехай ABC – прямокутний трикутник з прямим кутом С і гострим кутом при вершині A, що дорівнює . Косинусом гострого кута прямокутного трикутника називається відношення прилеглого катета до гіпотенузи. На рисунку або . Синусом кута називається відношення протилежного катета до гіпотенузи: або . Тангенсом кута називається […]...
- РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...
- Прямокутний трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Прямокутний трикутник Теорема Піфагора:...
- Трикутник і його елементи Розділ 1. Найпростіші геометричні фігури та їх властивості § 9. Трикутник і його елементи 292. На мал. 194 зображені трикутники ABD, ABC, ОВС. Проти кута C в трикутнику АВС лежить сторона АB, в трикутнику DBC – сторона BD. Прилеглими до кута С в трикутнику ABC є сторони АС і ВС, в трикутнику DBC – сторони […]...
- Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...
- Рівносторонній трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Рівносторонній трикутник Усі висоти, медіани й бісектриси мають однакову довжину. Вписане і описане коло мають спільний центр. Середня лінія трикутника – відрізок, що сполучає середини двох сторін трикутника. Теорема: Зовнішній кут трикутника – кут, суміжний із внутрішнім кутом трикутника. Теорема: Теорема косинусів: у будь-якому трикутнику зі сторонами а, b, с […]...
- Рівносторонній трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівносторонній трикутник Якщо всі сторони трикутника рівні, він називається Рівностороннім. На рисунку . Теорема 1. У рівносторонньому трикутнику всі кути рівні. Теорема 2. У рівносторонньому трикутнику висота, медіана, бісектриса, проведені з однієї вершини, збігаються. Теорема 3. У рівносторонньому трикутнику всі медіани (висоти, бісектриси) рівні між собою....
- Прямокутний паралелепіпед. Куб. Піраміда Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 25. Прямокутний паралелепіпед. Куб. Піраміда Сірникова коробочка, цеглина, дерев’яний брусок, ящик, пенал дають уявлення про геометричну фігуру, яка називається прямокутним паралелепіпедом (рис. 188). Рис. 188 Поверхня прямокутного паралелепіпеда складається із шести прямокутників, які називаються його гранями. Протилежні грані прямокутного паралелепіпеда попарно рівні. […]...
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- Трикутник і його види Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 2. ДОДАВАННЯ І ВІДНІМАННЯ НАТУРАЛЬНИХ ЧИСЕЛ 14. Трикутник і його види З усіх многокутників трикутники мають найменшу кількість сторін. Трикутники можна розрізняти за видом їх кутів. Якщо всі кути трикутника гострі, то його називають гострокутним трикутником (рис. 117). Якщо один із кутів трикутника прямий, то його […]...
- Кути, вписані в коло Геометрія Кути, пов’язані з колом Кути, вписані в коло Кут розбиває площину на дві частини. Кожна із цих частин називається Плоским кутом. Плоскі кути із спільними сторонами називаються Доповняльними. Якщо плоский кут є частиною півплощини, то його градусною мірою називається градусна міра звичайного кута з тими самими сторонами. Центральним кутом у колі називається плоский кут […]...
- Трикутник та його елементи Урок № 15 Тема. Трикутник та його елементи Мета: домогтися засвоєння учнями змісту понять: “трикутник”; “сторона, вершина, кут (внутрішній) трикутника”; “кут, протилежний стороні”; “кут, прилеглий до сторони”; “периметр трикутника”; “внутрішня та зовнішня область трикутника”. Сформувати вміння: – розпізнавати та називати елементи трикутників, зображених на рисунку; – за рисунком та символічним позначенням трикутника називати кути, протилежні […]...
- Теорема Піфагора Геометрія Трикутники Теорема Піфагора Теорема 1 (Піфагора). У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Правильною є і теорема, обернена до теореми Піфагора. Теорема 2 (обернена). Коли в трикутнику сторони a, b, c і , то цей трикутник є прямокутним з гіпотенузою c. Теорема 3. У прямокутному трикутнику будь-який із катетів менший за гіпотенузу. […]...
- Рівні трикутники. Висота, медіана, бісектриса трикутника § 2. Трикутники 6. Рівні трикутники. Висота, медіана, бісектриса трикутника Практичні завдання 132. 133. ВН – спільна висота трикутників ABD, ABC, BDC. ВН лежить поза трикутником BCD. 134. 135. 136. Вправи 137. 1) ME; 2) ∠E; 3) MK i KE; 4) ∠K i ∠E. 138. 1) ∠E; 2) ∠C i ∠E;3) CF; 4) CF і […]...
- Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...
- ТРИКУТНИК І ЙОГО ЕЛЕМЕНТИ Основна ідея, якою пройнята вся математика, – це ідея рівності. Г. Спенсер РОЗДІЛ 3 ТРИКУТНИКИ У цьому розділі ви повторите свої знання про трикутники, здобуті в попередніх класах, і дізнаєтеся про багато інших їх властивостей. Основне в розділі – три ознаки рівності трикутників Вони часто використовуються в геометрії. Тому від того, як добре ви вивчите […]...
- Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Рівняння. Кути. Прямокутник. Трикутник і його види УРОК 41 Тема. Рівняння. Кути. Прямокутник. Трикутник і його види Мета: підготовити учнів до тематичної контрольної роботи. Тип уроку: повторення і систематизація знань. Хід уроку I. Актуалізація опорних знань Усні вправи 1. Знайти корінь рівняння: 1) х + 15 = 29; 2) 30 – х = 17; 3) х – 12 = 19; 4) 12 […]...
- КОЛО І ТРИКУТНИК РОЗДІЛ 4 КОЛО І КРУГ. ГЕОМЕТРИЧНІ ПОБУДОВИ & 20. КОЛО І ТРИКУТНИК Коло і трикутник можуть не мати спільних точок або мати 1, 2, 3, 4, 5, 6 спільних точок (відповідні малюнки виконайте самостійно). Заслуговують на увагу випадки, коли коло проходить через усі три вершини трикутника або коли воно дотикається до всіх сторін трикутника. Розглянемо […]...
- Многокутник та його периметр. Трикутник. Види трикутників Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 21. Многокутник та його периметр. Трикутник. Види трикутників Якщо кінець ламаної збігається з її початком, то таку ламану називають замкненою. На малюнку 137 зображено замкнену ламану, що складається з п’яти ланок, причому ланки ламаної не перетинаються. Таку ламану називають многокутником. Зауважимо, що […]...
- Співвідношення між сторонами і кутами прямокутного трикутника Урок № 59 Тема. Співвідношення між сторонами і кутами прямокутного трикутника Мета: домогтися засвоєння учнями змісту правил знаходження невідомих сторін прямокутного трикутника, що випливають з означень тригонометричних функцій гострого кута; формувати вміння відтворювати зміст цих правил, а також застосовувати правила для знаходження невідомих сторін прямокутного трикутника. Закріплювати знання числових значень тригонометричних функцій кутів 30°, 45°, […]...
- Теорема Піфагора Урок № 34 Тема. Теорема Піфагора Мета: сформувати в учнів розуміння змісту теореми Піфагора та її доведення. Формувати вміння відтворювати зміст теореми Піфагора, застосовувати її формулювання для розв’язування задач на знаходження невідомих сторін прямокутних трикутників. Типу уроку: засвоєння нових знань. Наочність та обладнання: конспект “Теорема Піфагора”. Хід уроку I. Організаційний етап II. Перевірка домашнього завдання […]...
- Теорема синусів Геометрія Розв’язування трикутників Теорема синусів Теорема 1 (синусів). Сторони трикутника пропорційні до синусів протилежних кутів. У трикутнику, зображеному на рисунку, за теоремою синусів маємо: . Теорема 2. Якщо R – радіус кола, описаного навколо трикутника, то , або , де a – сторона трикутника, а – протилежний цій стороні кут. Теорема 3. У трикутнику проти […]...
- Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...