Головна ⇒ 📌Плани-конспекти уроків по фізиці ⇒ Релятивістський закон додавання швидкостей

Релятивістський закон додавання швидкостей

2-й семестр

МЕХАНІКА

5 . Релятивістська механіка

Урок 2/69

Тема. Релятивістський закон додавання швидкостей

Мета уроку: ознайомити учнів з релятивістським законом додавання швидкостей

Тип уроку: вивчення нового матеріалу

План уроку

Демонстрації

5 хв.

Фрагмент відеофільму “Принцип відносності Галілея”

Вивчення нового матеріалу

30 хв.

1. Класичний закон додавання швидкостей.

2. Релятивістський закон додавання швидкостей.

Відносність одночасності.

4. Відносність для двох подій понять “раніше” й “пізніше”

Закріплення вивченого матеріалу

10 хв.

1. Тренуємося розв’язувати задачі.

2. Контрольні запитання

ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

1. Класичний закон додавання швидкостей

Рух будь-якого тіла є відносним: його положення, швидкість, вид траєкторії залежать від того, відносно якої системи відліку (тіла відліку) цей рух розглядається. Щоб описати рух тіла, зручно обирати інерціальну систему відліку, тому що в цій системі відліку зміна швидкості тіла зумовлюється

лише дією на нього інших тіл.

O Інерціальними системами відліку називають такі системи відліку, у яких виконується перший закон Ньютона. Уперше твердження про рівноправність усіх інерціальних систем відліку висловив Галілей, тому його називають принципом відносності Галілея (або принципом відносності класичної фізики).

У всіх інерціальних системах відліку за однакових початкових умов усі механічні явища протікають однаково.

З цього принципу випливає, що не існує жодної виділеної системи відліку, яку можна було б назвати такою, що “перебуває в стані спокою”: усі інерціальні системи відліку цілком рівноправні. А це означає, що швидкість будь-якого тіла відносна: її можна визначити лише відносно певного тіла.

З принципу відносності Галілея випливає, що закони Ньютона мають ту саму форму в усіх ІСВ. При цьому якщо тіло рухається відносно інерціальної системи зі швидкістю 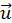‘, а сама система рухається зі швидкістю v відносно нерухомої системи, то швидкість й тіла відносно нерухомої системи відліку дорівнює:

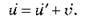
Це співвідношення називається законом додавання швидкостей Галілея (або класичним законом додавання швидкостей).

2. Релятивістський закон додавання швидкостей

Як узгодити твердження про незалежність швидкості світла від руху джерела з алгебраїчним додаванням звичайних швидкостей у механіці? Ейнштейн показав, що звичайна формула механіки для додавання швидкостей невірна й має бути змінена. Релятивістський закон додавання швидкостей має вигляд:

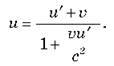
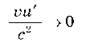Якщо << с, ця формула переходить у відому формулу перетворення Галілея для швидкості. Дійсно, якщо << с, то І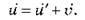

Якщо одна зі швидкостей дорівнює швидкості світла, наприклад ? с, то

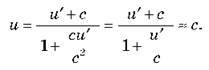
Цей результат демонструє той факт, що рух системи відліку не впливає на швидкість поширення світла в ній. Величина с відіграє роль гранично великої швидкості для будь-яких тіл або матеріальних сигналів.

3. Відносність одночасності

До початку XX ст. ніхто не сумнівався в тому, що час є абсолютним. Дві події, одночасні для жителів Землі, є одночасними для жителів будь-якої космічної цивілізації. Створення теорії відносності показало, що це не так.

Звернемося до уявного експерименту. Нехай прямолінійною ділянкою шляху рухається вагон завдовжки 6 600 000 км зі швидкістю 250 000 км/с. Припустімо, що в деякий момент у середині вагона загорілася лампочка. Спостерігач, який перебуває у вагоні, побачить, що світло дійде до передньої та задньої його стінок одночасно. Час поширення світла:

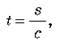
Де s – половина довжини вагона; с – швидкість світла:

Для спостерігача, який стоїть на платформі, швидкість поширення світла буде однаковою в усіх напрямах, але вагон відносно нього рухається. Світло, що поширювалося в напрямі руху вагона, наздоганяє його, тому світло пройде до зустрічі з передньою стінкою вагона шлях l1 = s + T1, де t1 – час поширення світла від джерела до передньої стінки вагона, а l1 = ct1. Звідси:

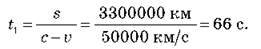
Світло, що поширюється проти напряму руху вагона, пройде до зустрічі з його задньою стінкою шлях l2 = s + T2, де t2 – час поширення світла до задньої стінки вагона. Звідси:

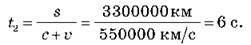
Отже, з погляду спостерігача, який стоїть на платформі, світло дійде до передньої та задньої стінок вагона не одночасно: до задньої стінки він дійде на 60 с швидше, ніж до передньої. Отже,

O дві події, одночасні в одній інерціальній системі відліку, не є одночасними в інший інерціальній системі відліку.

Одночасність – не абсолютна характеристика явищ. Різні спостерігачі можуть мати різні уявлення про одночасність подій.

Ейнштейн показав, що для кожної системи відліку, що рухається рівномірно й прямолінійно відносно іншої системи відліку, існує свій власний час.

Чому ж відносність одночасності подій практично неможливо спостерігати в повсякденному житті? Уявити собі це наочно, “відчути”, ми не можемо через те, що швидкість світла набагато більша за ті швидкості, з якими рухаємося ми. Одночасність може виявитися лише в процесі порівняння подій, розглянутих у системах відліку, які рухаються відносно одна одної зі швидкістю, що можна порівняти зі швидкістю світла.

4. Відносність для двох подій понять “раніше” й “пізніше”

Якщо змінити описаний уявний експеримент, й у тому ж вагоні, що рухається зі швидкістю 250 000 км/с, помістити лампочку не в середині вагона, а на відстані 2 200 000 км від передньої стінки вагона, то можна показати, що, з погляду спостерігача, який перебуває у вагоні, світло зустрінеться з передньою стінкою вагона раніше, ніж із задньою. З погляду спостерігача, який стоїть на платформі, світло зустрінеться із задньою стінкою вагона раніше, ніж з передньою.

Отже, поняття “раніше” й “пізніше” є відносними.

Розглянемо приклад: у деякій точці Галактики спалахнула “нова” зоря. Через певний час світло від цієї зорі дійде до спостерігача на Землі. Тут потрапляння світла в око спостерігача є наслідком народження “нової” зорі, а народження зорі є причиною потрапляння світла в око спостерігача. Ці дві події пов’язані причинно-наслідковим зв’язком. З якої б системи відліку не велося спостереження, поширення світла від зорі в жодному разі не може передувати її народженню, тобто наслідок ніколи не може настати раніше за причину.

Отже, якщо події пов’язані причинно-наслідковим зв’язком, то для них поняття “раніше” й “пізніше” є абсолютними.

Якщо події не пов’язані причинно-наслідковим зв’язком, як у прикладі з вагоном, то поняття “раніше” й “пізніше” є відносними. У цьому випадку зміна порядку чергування подій у часі не суперечить закону причинності, тобто наслідок не настає раніше за причину.

Запитання до учнів під час викладу нового матеріалу

1. Що ви розумієте під інерціальними системами відліку? Наведіть приклади.

2. Принцип відносності класичної фізики.

3. У чому полягають відмінності у формулюванні принципу відносності Галілея й принципу відносності Ейнштейна?

4. Порівняйте поняття одночасності в класичній фізиці й у теорії відносності.

5. У якому випадку поняття “раніше” й “пізніше” є відносними, а в якому – абсолютними?

6. Дві події в певній інерціальній системі відліку відбуваються в одній точці одночасно. Чи будуть ці події одночасними в іншій інерціальній системі відліку?

7. Чи можна стверджувати, що просторово розділені події, одночасні в одній інерціальній системі відліку, одночасні й у всіх інших інерціальних системах відліку?

ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ

1). Тренуємося розв’язувати задачі

1. Космічний корабель віддаляється від Землі з відносною швидкістю = 0,75 с. З нього стартує ракета (у напрямі від Землі) зі швидкістю u’= 0,75 с відносно корабля. Чому дорівнює швидкість ракети відносно Землі?

2. Дві частинки віддаляються від спостерігача зі швидкостями 0,7 с у протилежні боки. Якою є швидкість частинок відносно одна одної?

3. Дві фотонні ракети віддаляються одна від одної зі швидкістю 0,65 с відносно земного спостерігача. Чому дорівнює відносна швидкість ракет?

2). Контрольні запитання

1. За яких швидкостей руху релятивістський закон додавання швидкостей переходить у класичний закон?

2. У чому полягає принципова відмінність швидкості світла від швидкостей руху всіх тіл?

3. Що означає вислів “події А і В є одночасними”?

4. Доведіть, що поняття “раніше” й “пізніше” є відносними.

5. Які події називаються одночасними?

Що ми дізналися на уроці

– У всіх інерціальних системах відліку за однакових початкових умов усі механічні явища протікають однаково.

– Класичний закон додавання швидкостей:

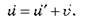
– Релятивістський закон додавання швидкостей:

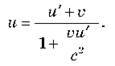
– Подія – це спрощена модель такого явища, яке в заданій системі відліку можна вважати таким, що відбувається в певній точці простору в певний момент часу.

– Події, одночасні в одній системі відліку, виявляються неодночасними в іншій системі відліку, яка рухається рівномірно й прямолінійно відносно першої, тобто одночасність – поняття відносне.

Домашнє завдання

1. П.: § 48.

2. 36.:

Р1) – 22.5; 22.6;

Р2) – 22.7; 22.20; 22.21;

Р3) – 22.33, 22.34; 22.39.