Рівність геометричних фігур

Розділ 1. Найпростіші геометричні фігури та їх властивості

§ 11. Рівність геометричних фігур

397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F.

398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину.

399. Кути ABC і MON сумістити не можна, оскільки вони мають різні градусні міри.

400. XY = AB = 17. XZ = АС = 10, YZ = BC = 9, ∠X = ∠A, ∠Y = ∠B, ∠Z = ∠C.

401. AB = AC.

402.

403.

404.

1) Відрізки

АО i OB можна сумістити, бо вони мають рівні довжини.

2) Відрізки АО і AB не можна сумістити, бо вони мають різні довжини.

3) Відрізки AB і OB не можна сумістити, бо вони мають різні довжини.

405.

1) Кути АОС і СОВ можна сумістити, бо вони мають рівні градусні міри.

2) Кути АОС і АОВ не можна сумістити, бо вони мають різні градусні міри.

3) Кути АОВ і СОВ не можна сумістити, бо вони мають різні градусні міри.

406. 1) Можна, бо АВ = СВ, 3,4 см = 3,4 см.

2) Не можна, бо АВ ≠ СО, 5 см + 6 см.

3) Не можна, бо AB ≠ CD, 15 см + 15 мм.

407. 1) Неможна, бо 60° ≠ 61°.

2) Можна, бо 73° = 73°.

3) Не можна,

бо 107°58′ ≠ 107°69′.

408. Так, квадрати сумістяться, бо AB = А1В1, ВС = B1C1, CD = С1D1, AD = A1D1, ∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1.

409. 1) Так; 2) так; 3) так, бо вони рівні; 4) не завжди, можна сумістити, якщо вони рівні.

410. Так, кола сумістяться.

411. 1) Точки С і С1 не сумістяться, бо АС ≠ А1С1. 2) Точки В і В1 не сумістяться, бо AB ≠ А1В1. 3) Відрізки EF і E1F1 сумістяться, бо EF = E1F1.

412. 1) Ні; 2) ні; 3) ні.

413. 1) АВ = A1B1, АС = А1С1, ВС = В1С1; 2) ∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1.

414. ?АВС = ?А1В1С1.

1) A1B1 = AB = 6 см, B1C1 = ВС = 7 см, А1С1 = АС = 8 см;

2) ∠A = ∠A1 = 65°, ∠B = ∠B1 = 80°, ∠C = ∠C1 = 35°.

415. 1) Оскільки? ABC = ?А1В1С1, то ∠A1 = ∠A = 42°, ∠B1 = ∠B = 80°, ∠C1 = ∠C = 180° – 42° – 80° = 58°.

2) Оскільки? ABC = ?A1B1C1, то ∠B1 = ∠B = 65°, ∠C1 = ∠C = 45°, ∠A1 = ∠A = 180° – 65° – 45° = 70°.

416. 1) Оскільки? ABC = ?A1B1C1, то P? А1В1С1 = А1В1 + B1C1 + А1С1 = AB + BC + AC = 7 см + 9 см + 11 см = 27 см.

2) Оскільки? ABC = ?A1B1C1, то P? А1В1С1 = А1В1 + B1C1 + А1С1 = AB + BC + AC = 14 см + 15 см + 17 см = 46 см.

3) Оскільки? ABC = ?A1B1C1, то P? А1В1С1 = А1В1 + B1C1 + А1С1 = AB + BC + AC = 1,3 дм + 2,1 дм + 20 см = 1,3 дм + 2,1 дм + 2 дм = 5,4 дм.

Відповідь: 1) 27 см; 2) 46 см; 3) 5,4 дм.

417.

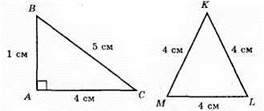
Трикутники, які мають рівні периметри, не завжди рівні.

P? АВС = 3 см + 5 см + 4 см = 12 см.

P? MKL = 4 см + 4 см + 4 см = 12 см.

P? АВС = P? MKL > але? AВС ≠ ?MKL.

418. 1) А1В1 = 11 см, АС = 16 см, B1C1 = 14 см; 2) ∠B1 = 60°, ∠A = 60°, ∠C = 70°.

419. AB = А1В1 = A2B2 = 4,2 см, BC = B1C1 = B2C2 = 2 см, А1С1 = А2С2 = AC = 6,3 см, ∠A1 = ∠A2 = ∠A = 20°, ∠B = ∠B2 = ∠B1 = 115°, ∠C = ∠C1 = ∠C2 = 45°.

420.

421.

422.

Застосуйте на практиці

423.

Оскільки OB ⊥ AC, BP ⊥ AK, TO ∠OBP = ∠BAK.

424. KL = AB, ML = CB, ∠L = ∠B. Oтже, ?KLM = ?АВС за першою ознакою рівності трикутників.

425. Оскільки AB ≠ DF, АС = DE, ∠A = ∠D, то? АВС ≠ ?DEF.

426. ?KML = ?АВС.

427. Оскільки DE = АВ, ∠D = ∠A, ∠E = ∠B, то? DEF = ?ABC за другою ознакою рівності трикутників.

428. LE = LB, LD = LA, ED ≠ BA. Отже, ?ABC ≠ ?PMN.

429.

?ABC = ?PMN.

430. Мал. 250. ?АВD = ?CBD запертою ознакою рівності трикутників, оскільки AD = CD, ∠BDA = ∠BDC, BD – спільна сторона.

Мал. 252. ?ABD = ?CBD за першою ознакою рівності трикутників, оскільки AB = CB, ∠ABD = ∠CBD, BD – спільна сторона.

Мал. 252. ?АВО = ?DCO за першою ознакою рівності трикутників, оскільки BO = CO, AO = DO, ∠BOA = ∠COD – як вертикальні кути.

431. Оскільки ∠A = ∠E, AB = EF, АС = DE, то? ABC = ?EFD за першою ознакою рівності трикутників, тоді ∠B = ∠F.

432.

?ABC	AB = 15 см, ВС = 16 см, ∠B = 120°	AB = 16 см, AC = 19 см, ∠A = 13°
?KLM	KL = 5 см, LM = 16 см, ∠L = 120°	KL = 16 см, KM = 19 см, ∠K = 13°
?DEF	DE = 5 см, EF = 16 см, ∠E = 120°	DE = 16 см, DF = 19 см, ∠D = 13°

433. АС = KL, CB = LM, ∠C = ∠L, то? АСВ = ?KLM за першою ознакою рівності трикутників, тоді КМ = АВ = 7.

434.

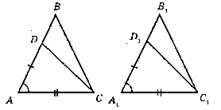
Оскільки AD = A1D1, AC = A1C1, ∠A = ∠A1, то? ADC = ?A1D1C1 за першою ознакою рівності трикутників.

435.

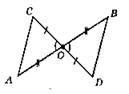
1) Оскільки CO = DO, AO = BO, ∠AOC = ∠BOD – як вертикальні кути, то? АОС = ?BOD за першою ознакою рівності трикутників.

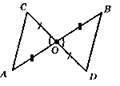
2) Оскільки АО = BO, CO = DO, ∠BOC = ∠AOD то? ВОС = ?АОD за першою ознакою рівності трикутників.

436. Оскільки BD – бісектриса ∠ABC, то ∠CBD = ∠ABD.

?ABD = ?CBD за першою ознакою рівності трикутників, оскільки AB = ВС, BD – спільна сторона. ∠CBD = ∠ABD. Із рівності трикутників маємо:

1) AD = CD; 2) ∠BCD = ∠BAD = 130°.

437.

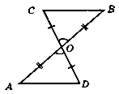
Оскільки AO = OB, CO = OD, ∠COB = ∠DOA – як вертикальні кути, то? СОВ = ?DOA за першою ознакою рівності трикутників.

Із рівності трикутників маємо:

1) ВС = AD = 5 см; 2) ∠ABC = ∠BAD = 65°.

438. Мал. 255. Оскільки ∠ABD = ∠CBD, ∠ADB = ∠CDB, BD – спільна сторона, то? BAD = ?BCD за другою ознакою рівності трикутників.

Мал. 256. Оскільки ∠BAD = ∠CDA – як сума двох рівних кутів, ∠CAD = ∠BDA, AD – спільна сторона, то? ABD = ?DCA за другою ознакою рівності трикутників.

Мал. 257. Оскільки АО = CO, ∠A = ∠C, ∠BOA = ∠DOC – як вертикальні кути, то? АBО = ?СDO за другою ознакою рівності трикутників.

439. Оскільки AB = FF, ∠A = ∠F, ∠B = ∠F, то? ABC = ?EFD за другою ознакою рівності трикутників, тоді ∠F = ∠C.

440.

?ABC	AB = 7 см, ∠A = 60°, ∠B = 41°	АС = 13 см, ∠A = 27°48′, ∠C = 92°
?DEF	DE = 7 см, ∠D = 60°, ∠E = 41°	DF = 13 см, ∠D = 27°48‘, ∠F = 92°
?PMN	PM = 7 см, ∠P = 60°, ∠M = 41°	PN = 13 см, ∠P = 27°48‘, ∠N = 92°

441. На мал. 258. Оскільки AB = EF, ∠A = ∠E, ∠B = ∠F, то? АВС = ?EFD за другою ознакою рівності трикутників. Із рівності трикутників випливає, що ∠B = ∠C = 40°.

На мал. 259. Ос кільки AB = QR, ∠A = ∠Q, ∠B = ∠R, то? ABC = ?QRP за другою ознакою рівності трикутників, тоді OР = АС = 12 см.

442. Оскільки AB = DP, ∠A = ∠D, ∠B = ∠P, TO? ABC = ?DPM за другою ознакою рівності трикутників. Із рівності трикутників маємо:

1) AB = DP = 6,2 см; 2) ∠D = ∠A = 54°; 3) ∠B = ∠P = 46°39′; 4) PM = BC = 85 мм.

443.

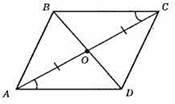
Оскільки АО = OC, ∠OCB = ∠OAD і ∠BOC = ∠DOA – як вертикальні кути, то? СОВ = ?AOD за другою ознакою рівності трикутників.

444. Оскільки ∠AOB = ∠ADC, AD – спільна сторона, ∠BAD = ∠CAD, бо AD – бісектриса кута САВ, то? ABD = ?ACD за другою ознакою рівності трикутників.

445.

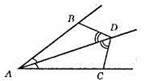
Оскільки ∠BDA = ∠CDA, ∠BAD = ∠CAD, бо AD – бісектриса кута А, AB – спільна сторона, то? ABD = ?ACD за другою ознакою рівності трикутників.

446. Оскільки АО = СО, BO = DO, ∠AOB = ∠COD як вертикальні кути, то? АОВ = ?COD за першою ознакою рівності трикутників.

Із рівності трикутників маємо ∠ABO = ∠CDO, а ці кути є внутрішніми різносторонніми при прямих AB і CD і січній BD. Отже, AB || CD.

447. Оскільки ВС = AD, ∠DAC = ∠ACB, АС – спільна, то? ABC = ?CDA за першою ознакою рівності трикутників. Із рівності трикутників маємо: ∠BAC = ∠DCA, які є внутрішніми різносторонніми при прямих AB і CD і січній АС, отже, AB || DC.

448. Оскільки ВС || AD, то ∠DAC = ∠BCA – як внутрішні різносторонні кути при паралельних прямих ВС і AD і січній АС.

?ABC = ?ADC за першою ознакою рівності трикутників, оскільки ВС = AD, ∠DAC = ∠BCA, АС – спільна сторона.

449.

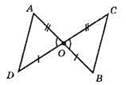
Оскільки АО = ОС, OB = OD (бо AB = CD за умовою i АО = ОС), ∠AOD = ∠COB – як вертикальні кути, то? ВОС = ?DOA. Із рівності трикутників випливає, що ∠ABC = ∠ADC.

450.

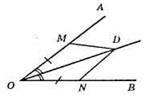
Оскільки ОМ = ON, то ∠MOD = ∠NOD (бо OD – бісектриса кута A), OD – спільна сторона, то? MOD = ?NOD запертою ознакою рівності трикутників. Із рівності трикутників випливає, що DM =DN.

451.

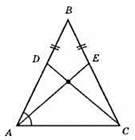
Розглянемо? АВЕ і? CBD. BE = BD, ВС = ВА – як бічні сторони рівнобедреного трикутника, ∠DBE – спільний. Отже, ?АВЕ = ?CBD за першою ознакою рівності трикутників. Із рівності трикутників випливає: 1) AE = CD; 2) ∠AEC = ∠ADC – як суміжні кути до рівних кутів АЕВ і В DC.

452. Розглянемо трикутники OAD і OCD. У них ОА = ОС, OD = OB, ∠O – спільний. ?OAD = ?OCD за першою ознакою рівності трикутників. Із рівності трикутників маємо: 1) AD = ВС; 2) ∠OAD =∠OCB, тоді ∠DAB = ∠BCD – як суміжні до рівних кутів OAD і ОСВ.

453.

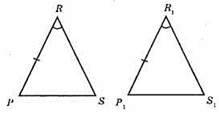
Нехай PRS і Р1R1S1- рівнобедрені трикутники (PR = RS, P1R1= R1S1).

У них PR = Р1R1, ∠R = ∠R1. ?PRS = ?P1R1S1 (оскільки PR = Р1R1, ∠R = ∠R1, RS = R1S1) за першою ознакою рівності трикутників.

454.

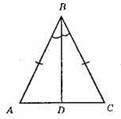
Нехай BD – бісектриса рівнобедреного трикутника ABC (AB = ВС).

Оскільки АВ = ВС, ∠ABD = ∠CBD (оскільки BD – бісектриса кута В), BD – спільна сторона, то? ABD = ?CBD. Із рівності трикутників випливає, що AD = DC, тобто BD – є медіаною трикутника АВС.

455. Оскільки BO = OD, ∠BAO = ∠DCO (як внутрішні різносторонні кути при паралельних прямих AB і DC та січною АС), ∠АВО = ∠CDO (як внутрішні різносторонні кути при паралельних прямихAB і DC і січною BD), то? АОВ = ?COD за другою ознакою рівності трикутників.

456. Оскільки АО = ОС і ∠ОАВ = ∠OCD – за умовою, ∠AOB = ∠DOC – як вертикальні кути, то? AOB = ?СОD за другою ознакою рівності трикутників. Із рівності трикутників маємо: 1) AB = CD = 10 CM; 2) OB = OD = 3 CM, BD = BO + OD = 3 CM + 3 CM = б CM.

457. І випадок (задано гострий кут)

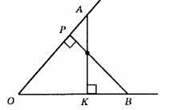
ОА = OB – за умовою. AK ⊥ OB, BP ⊥ ОА, тобто ∠АКО = ∠ВРО = 90°, ∠О – спільний. Отже, ?ОАК = ?ОВР за другою ознакою рівності трикутників. Із рівності трикутників маємо: AK = ВР.

II випадок (задано прямий кут)

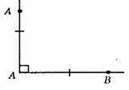
Оскільки ∠AOB = 90°, то AO ⊥ ВО, АО = ВО, то перпендикуляри рівні.

III випадок (задано тупий кут)

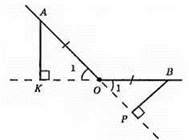
Розглянемо? ОАК і? ОВР. У них АО = OB – за умовою, ∠AOK = ∠BOP (як вертикальні кути), ∠KAO = ∠PBO (бо кожен з них дорівнює 90° – ∠1), отже, ?ОАК = ?ОВР за другою ознакою рівності трикутників. Із рівності трикутників маємо: АК = ВР.

458.

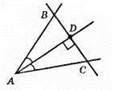
Нехай AD – бісектриса кута А, АD ⊥ BC. Розглянемо? ABD і? ADC. ∠BAD = ∠CAD, оскільки AD – бісектриса кута A, ∠ADB = 90°, ∠ADC = 90°. AD – спільна сторона. Отже, ?ABD = ?ACD за другою ознакою рівності трикутників. Із рівності трикутників AB = АС, тобто? ABC – рівнобедрений.

459.

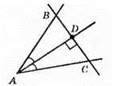
Нехай АD – бісектриса кута А і АD ⊥ ВС. ?ABD = ?ACD, оскільки ∠BAD = ∠CAD (бо АХ) – бісектриса кута A), ∠ADB = ∠ADC = 90° (бо АD ⊥ ВС). Із рівності трикутників маємо: AB = АС.

460.

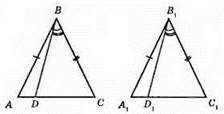
?ABC = ?A1B1C1 за першою ознакою рівності трикутників (оскільки AB = A1B1, ВС = B1C1, ∠B = ∠B1 за умовою). Із рівності трикутників маємо, що ∠A = ∠A1. Розглянемо? ABD і? A1B1D1: ∠A =∠A1, AB = A1B1, ∠ABD = ∠A1B1D1 – як різниця рівних кутів. Отже, ?ABD = ?A1B1D1 за другою ознакою рівності трикутників.

461.

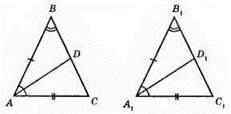
?ABC = ?A1B1C1 за другою ознакою рівності трикутників (оскільки AB = A1B1, ∠A = ∠A1, ∠B = ∠B1). Із рівності трикутників маємо: ВС = B1C1, AC = A1C1, ∠C = ∠C1.

1) ?ACD = ?A1C1D1 за першою ознакою рівності трикутників, оскільки АС = A1C1, ∠C = ∠C1, CD = C1D1 (як половини рівних сторін ВС і B1C1).

2) ?ABD = ?A1B1D1 за першою ознакою рівності трикутників, оскільки AB = A1B1, ∠B = ∠B1, BD = B1D1 (як половини рівних сторін ВС і B1C1).

462.

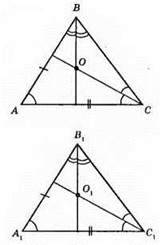
?ABC = ?А1В1С1 за першою ознакою рівності трикутників. Із рівності трикутників маємо: BC = B1C1, ∠B = ∠B1, ∠C = ∠C1. Розглянемо? ВОС і? В1O1С1. У них ВС = B1C1, ∠OBC = ∠O1B1С1 – як половини рівних кутів В і B1, ∠OCB = ∠O1C1B1 – як половини рівних кутів С і С1. Отже, ?ВОС = ?B1O1C1 за другою ознакою рівності трикутників.

463. За умовою ОА = ОС, OD = OB, ∠O – спільний. Тоді? AOD = ?СОВ. Отже, ∠OAD = ∠OCB, ∠ADO = ∠CBO, CD = OD – ОС, AB = OB – ОА і AB = CD, ∠BAM = ∠DCM як суміжні до рівних кутів OADі ОСВ. Тоді? АВМ = ?СОМ за другою ознакою рівності трикутників.

464.

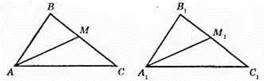
Нехай? ABC = ?А1В1С1, AM = А1М1. Оскільки? ABC = ?А1В1С1, то AB = А1В1, ∠B = ∠B1, BC = В1С1.

Розглянемо? ABM i? A1B1M1. У них АВ = А1В1, ∠B = ∠B1, ВМ = В1M1 – як половини рівних сторін ВС і B1C1. Отже, ?АВМ = ?А1В1М1 за першою ознакою рівності трикутників. З рівності трикутників маємо: AM = А1М1, тобто у рівних трикутників медіани, проведені до рівних сторін, рівні.

465.

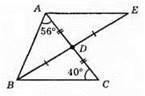
Оскільки BD – медіана, то AD = CD, DE = BD за побудовою.

Отже, ?ADE = ?CDB за другою ознакою. Із рівності трикутників маємо: ∠DAE = ∠DCB = 40°. Тоді ∠BAE = ∠BAD + ∠DAE = 56° + 40° = 96°.

Відповідь: 96°.

466.

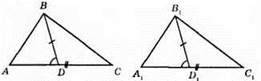
Нехай АС = A1C1, BD і B1D1 – медіани, BD = B1D1, ∠ADB = ∠A1D1B1.

Доведемо, що? ABC = ?А1В1С1.

?ADB = ?A1D1B1 за першою ознакою рівності трикутників, оскільки AD = A1D1 – як половини рівних сторін, BD = B1D1 – за умовою, ∠ADB = ∠A1D1B1.

З рівності трикутників маємо: АВ = А1В1, ∠A = ∠A1.

?ABC = ?A1B1C1 за першою ознакою рівності трикутників, оскільки АС = A1С1 за умовою, AB = A1B1 за доведеним, ∠A = ∠A1 за доведеним.

467. 1)

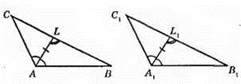
Нехай ∠A = ∠A1, AL = A1L1, ∠ALB = ∠A1L1B1.

Доведемо, що? ABC = ?А1В1С1.

?ALB = ?A1L1B1 за другою ознакою рівності трикутників, оскільки AL = A1L1 – за умовою, ∠ALB = ∠A1L1B1 – за умовою, ∠LAB = ∠L1A1B1 – як половини рівних кутів. З рівності трикутників маємо: AB = A1B1, LB = L1B1.

Розглянемо трикутники ABC і А1В1С1: AB = А1В1, ∠A = ∠A1, ∠B = ∠B1. Отже, ?ABC = ?А1В1С1 за другою ознакою рівності трикутників.

2)

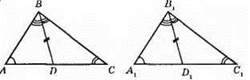
Нехай ∠A = ∠A1, ∠C = ∠C1, BD та В1D1 – бісектриси, BD = В1D1.

Доведемо, що? ABC = ?А1В1С1.

За теоремою про суму кутів трикутника ∠A + ∠C + ∠B = 180°, ∠B – 180° – (∠A + ∠B), ∠B1 = 180° – (∠A1 + ∠B1), отже, ∠B = ∠B1.

Оскільки ∠A = ∠A1 за умовою, ∠ABD = ∠A1D1B1 – як половини рівних кутів B і B1, то ∠ABD = ∠A1D1B1.

?ABD = ?A1B1D1 за другою ознакою рівності трикутників, оскільки BD = B1D1 – за умовою, ∠ABD = ∠A1B1D1 – за доведеним, ∠ADB = ∠A1D1B1 – за доведеним.

Із рівності трикутників випливає, що AB = A1B1. Тоді? ABC = ?А1В1С1 за другою ознакою рівності трикутників, оскільки АВ = А1В1 – за доведеним, ∠A = ∠A1 – за умовою, ∠B = ∠B1 – за доведеним.

3)

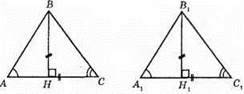
Нехай ∠A = ∠A1, ∠C = ∠C1, ВН та В1Н1 – висоти, BH = В1H1.

Доведемо, що? ABC = ?А1В1С1.

?АВН = ?А1В1Н1, оскільки у них ∠AHB = ∠A1H1B1 = 90°, ВН = B1H1, ∠ABH = ∠A1B1H1 (оскільки ∠ABH = 90° – ∠A, ∠A1B1H1 = 90° – ∠A1). Із рівності трикутників маємо АВ = A1B1, ∠ABH – ∠A1B1H1.

?CBH = ?C1B1H1, оскільки ∠BHC = ∠B1H1C1 = 90°, BH = B1H1, ∠CBH = ∠C1B1H1 (оскільки ∠CBH = 90° – ∠C, ∠C1B1H1 = 90° – ∠C1).

Із рівності трикутників маємо: ВС = B1C1, ∠CBH = ∠C1B1H1.

Розглянемо трикутники ABC і A1B1C1. У них AB = А1В1, ВС = В1С1, ∠ABC = ∠А1В1С1 (як суми рівних кутів ∠ABH = ∠A1B1H1, ∠CBH = ∠C1B1H1). Отже, ?ABC = ?А1В1С1.

468.

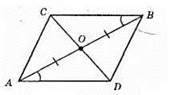
?CBO = ?DAO за другою ознакою рівності трикутників, оскільки AO = ВО (за умовою), ∠CBO = ∠DAO (за умовою), ∠COB = ∠DOA – як вертикальні кути.

Із рівності трикутників маємо: CO = DO. Розглянемо? СОА і? DOB. АО = ВО – за умовою, CO = OD – за доведеним, ∠AOC = ∠BOD – як вертикальні. Отже, ?АОС = ?BOD за першою ознакою рівності трикутників.

469. ?АОВ = ?DOC за першою ознакою рівності трикутників, оскільки AO = OD, ВО = ОС, ∠AOB = ∠DOC – як вертикальні кути. Із рівності цих трикутників випливає, що ∠A = ∠D.

Розглянемо? AMО і? DNO: AO = OD – за умовою, ∠A = ∠D – за доведеним, ∠AOM = ∠DON – як вертикальні кути. Отже, ?АОМ = ?DON за другою ознакою рівності трикутників. Із рівності цих трикутників випливає, що MO = ON.

470.

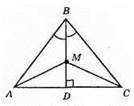
?ABD = ?CBD за другою ознакою рівності трикутників, оскільки BD – спільна сторона, ∠ADB = ∠CDB = 90° (бо BD – висота), ∠ABD = ∠CBD – за умовою. З рівності трикутників випливає, що AD= DC.

Розглянемо? AMD і? CMD: AD = DC, ∠ADM = ∠CDM = 90°, MD – спільна сторона. Отже, ?AMD = ?CMD за першою ознакою рівності трикутників. Із рівності трикутників випливає, що AM = CM.

471. ?OAD = ?ОСВ за першою ознакою рівності трикутників, оскільки ∠O – спільний, ОА = ОС – за умовою, OD = OB (як суми рівних відрізків). Із рівності трикутників випливає, що ∠ODA =∠OBC.

?CDM = ?АВМ за другою ознакою рівності трикутників, оскільки ∠ODA = ∠OBC – за доведеним, CD = AB – за умовою, ∠CMD = ∠AMB – як вертикальні, тоді ∠MCD = ∠MAB. Із рівності трикутників маємо: DM = ВМ. Розглянемо трикутники ODM і ОВМ: DM = ВМ – за умовою, ∠CDM = ∠ABM – за доведеним, OD = OB – як суми рівних відрізків. Отже, ?ODM = ?ОВМ за першою ознакою рівності трикутників. Із рівності трикутників маємо: ∠DOM = ∠BOM, тобто ОМ – бісектриса кута О.

472.

Нехай ∠A = ∠A1, AL = A1L1, AC = A1C1. Доведемо, що? ABC = ?A1B1C1.

?ALC = ?A1L1C1 – за першою ознакою рівності трикутників, оскільки AL = A1L1 – за умовою, АС = А1С1 – за умовою, ∠LAC = ∠L1A1C1 – як половини рівних кутів. З рівності трикутників маємо:∠C = ∠C1.

Розглянемо? ABC і? A1B1C1: АС = А1С1 – за умовою, ∠A = ∠A1 – за умовою, ∠C = ∠C1 – за доведеним. Отже, ?АВС = ?A1B1C1 – за другою ознакою рівності трикутників..