Рівняння із двома змінними та його розв’язок
Урок № 69
Тема. Рівняння із двома змінними та його розв’язок
Мета: сформувати уявлення про рівняння із двома змінними та його розв’язки; усвідомити зміст поняття “графік рівняння із двома змінними”; виробити вміння: відбирати перевіркою розв’язки рівняння із двома змінними; працювати з готовим графіком рівняння із двома змінними; перетворювати рівняння виду у = f(x) та обчислювати розв’язки рівняння із двома змінними.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього
@ Учитель збирає зошити, щоб перевірити якість корекційної роботи учнів та творче завдання.
III. Актуалізація опорних знань
Виконання усних вправ
1. Розв’яжіть рівняння:
3х = 6; 3х + 2 = 6; 6х = 3; 6 + х = 3; 6 + x = 2x – x + 6, 3х + 5 = 3х + 7.
Що означає “розв’язати рівняння”?
2. Складіть рівняння за умовою задачі:
1) довжина прямокутника х, ширина 3 м, а периметр 20 м;
2) ширина прямокутника х, довжина на 4 м більша, а периметр 20 м;
3) ширина прямокутника х, довжина у м, а периметр 20 м.
Якщо можна, розв’яжіть рівняння, знайдіть довжини сторін прямокутника.
3. Чи належить графіку функції
4. Чи є дана рівність правильною: 2 – 1 + 3 – (-1) = 5; 2 – 0,5 + 3 – (-1) = -2?
IV. Формулювання мети й завдань уроку
Після повторення основних понять, вивчених у темі “Лінійні рівняння з однією змінною”, та виконання усних вправ і складання рівнянь разом з учнями формулюємо мету: познайомитись із тим новим видом рівняння, що зустрівся нам під час розв’язування одного із завдань.
V. Вивчення нового матеріалу
@ Нове поняття “рівняння з двома змінними” вводиться на прикладах (так само, як і “рівняння з однією змінною”), а потім формулюється означення рівняння з двома змінними та означення розв’язку такого рівняння як впорядкованої пари чисел – значень змінних, що перетворюють рівняння на правильну рівність, так само, як і корінь рівняння з однією змінною. Це означення повинно бути добре зрозумілим усім учням. Поняття рівносильних рівнянь із двома змінними будується на відомих учням поняттях рівносильних рівнянь та властивостях рівносильних рівнянь. І взагалі, автор вважає, що формування нових знань учнів буде більш результативним, а знання – більш свідомими, якщо під час вивчення нового матеріалу звернутись до прийому аналогії (рівняння з однією зміною). З цього випадає лише поняття графіка рівняння з однією змінною, але це є винятком, що підтверджує справедливість правила. Тому й записи в зошитах учнів можуть мати вигляд порівняльної таблиці, в якій виділено ключові слова.
Конспект 21 | ||
Вид твердження | Рівняння з однією змінною | Рівняння з двома змінними |
1) Приклад | Х + 5 = 8 | Х + у = 8 |
2) Опис | Рівність, що містить невідоме число, позначене буквою (змінна) | Рівність, що містить два невідомих числа, позначених буквою (змінні) |
3) Супутні поняття | Корінь рівняння із першою змінною – значення змінної, що перетворює рівняння на правильну рівність | Розв’язання рівняння із двома змінними – впорядкована пара чисел (х;у), за яких рівняння перетворюється на правильну рівність |
4) Рівносильні | Рівняння з однією змінною – мають однакові корені або взагалі не мають коренів | Рівняння з двома змінними – мають одні й ті самі розв’язки або обидва не мають розв’язків |
5) Властивості рівносильних рівнянь | Однакові | |
6) Графік | ? | Фігура, що складається з точок (х; у), таких, що їх координати – розв’язки рівняння |
VI. Закріплення матеріалу. Вироблення вмінь
Виконання усних вправ
1. Чи є розв’язком рівняння х – 2у = 6 пара чисел (0; 0); (2; -2); (8; 1); (0; 3); (15; 4); (6; 0); (5; -5,5)?
2. Точки А(…; 0); В(0; …); С(1; …); D(…; -3) належать графіку рівняння 3х – у = 6. Знайдіть пропущені координати.
3. Виразіть змінну у через змінну х (зведіть рівняння до вигляду y = f(x)) шляхом виконання тотожних перетворень: х + у = 1; 5х + 5у = 0;
Х – у = 2. За утвореною формулою знайдіть два розв’язки кожного рівняння.
Виконання письмових вправ
1. Пари значень х та у внесено в таблицю. Які з них є розв’язками рівняння 1) х2 + у2 = 25; 2) х2 – у2=7?
Х | -5 | -4 | -3 | -1 | 0 | 3 | 4 | 5 |
У | 0 | 3 | 4 | 1 | -5 | 4 | -3 | 0 |
2. Виразіть із рівняння змінну у через змінну х. Використовуючи утворену формулу, знайдіть три будь-які розв’язки рівняння:
1) х + у = 27;
2) 2х – у = 4,5;
3) 3х + 2у = 12;
4) 5у – 2х = 1.
3. Які з точок А(-2; -5); В(4; 1); С(1; -4); D(2; 2) належать графіку рівняння х2 – 2ху + у3 = 0?
4. Доведіть, що рівняння:
1) х2 + у2 = -1 не має розв’язків;
2) х2 + у2 = 0 має тільки один розв’язок.
Додатково. Серед розв’язків рівняння х + 2у = 18 знайдіть таку пару, яка б складалась із двох однакових чисел.
VII. Підсумки уроку
Контрольні запитання
1. Що називається розв’язком рівняння з двома змінними? Чи є пара (2; 1) розв’язком рівнянь: 2у – х2 = -2; 3х – у = 4; х2 – у3 = 3; ху = 3?
2. Які рівняння з двома змінними називають рівносильними? Наведіть приклад.
3. Що таке графік рівняння з двома змінними?
VIII. Домашнє завдання
№ 1. Вивчіть зміст основних понять та складіть алгоритми:
А) “Як перевірити, чи є пара (х;у) розв’язком рівняння з двома змінними”;
Б) “Як знайти розв’язки рівняння з двома змінними”.
№ 2. Виразивши змінну у через х, знайдіть три будь-які розв’язки рівняння:
1) ху – 12 = 0; 2) 3х – у = 10.
№ 3. Які з точок А(-3; 12); В(2; -1); С(0; 3) належать графіку рівняння х2 – у + 3 = 0?
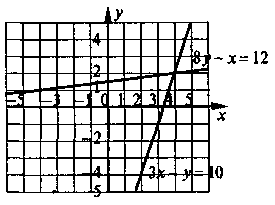
№ 4. На рисунку побудовані графіки рівнянь 3х – у = 10 і 8у – х = 12. Для кожного з рівнянь знайдіть за його графіком декілька розв’язків. Використовуючи рисунок, укажіть таку пару чисел, яка є розв’язком як першого, так і другого рівняння, перевірте відповідь обчисленням.