Головна ⇒ 📌Довідник з геометрії ⇒ Рівняння кола
Рівняння кола
Геометрія
Декартові координати на площині
Рівняння кола
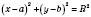 – рівняння кола з центром у точці
– рівняння кола з центром у точці 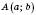 і радіусом R.
і радіусом R.
Зверніть увагу:
рівняння 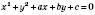 ,
,
де 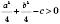 , задає коло й може бути зведеним до стандартного виду.
, задає коло й може бути зведеним до стандартного виду.
Related posts:
- Рівняння кола УРОК № 26 Тема. Рівняння кола Мета уроку: виведення рівняння кола. Формування вмінь учнів використовувати рівняння кола до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння кола. Розпізнають рівняння кола. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Взаємне розміщення кола і прямої – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Взаємне розміщення кола і прямої Коло і пряма не мають спільних точок. Коло і пряма мають одну спільну точку. А – дотична А – точка дотику Коло і пряма мають дві спільні точки. А – січна Рівняння кола (х – а)2 + (y – b)2 = R2, де (а, b) […]...
- Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180° Геометрія Декартові координати на площині Означення синуса, косинуса, тангенса, котангенса для будьякого кута від 0° до 180° Візьмемо коло на площині Oxy з центром у початку координат і радіусом R. Відкладемо від додатної півосі Ox кут у верхню півплощину (див. рисунок нижче). Точку перетину сторони кута з колом назвемо . Вона має координати . Тоді […]...
- Метод координат. Рівняння сфери, площини, прямої Завдання 2 1. 1) Рівняння сфери, усі точки якої рівновіддалені від початку координат на 1 од. має вигляд х2 + у2 + z2= 1. 2) Оскільки центр сфери – початок координат і вона перетинає ось Оz у точці (0; 0; 1), то вона має радіус 1, а значить, її рівняння; х2 + у2 + z2 […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Рівняння сфери, площини і прямої 79. (x – 1)2 + у2 + (2 – 4)2 = 25. 80. A(10; 0; 0), В(0; 10; 0), С(0; 0; 10). 81. M(3; 2; -1) не належить сфері. X2+ у2 + z2 – 2х + 4у – 6z – 2 = 0, бо 32 + 22 + (-1)2 – 2 × 3 + 4 […]...
- Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...
- Рівняння прямої Геометрія Декартові координати на площині Рівняння прямої Будь-яка пряма в декартових координатах x, y має рівняння виду: , де a, b, c – деякі числа. Знаходження координат точки перетину прямих та випадки розміщення прямої відносно системи координат описано в розділі “Алгебра. 8 клас” (“Лінійна функція”). Рівняння прямої, яка перетинає осі координат в точках і , […]...
- Відстань між точками Геометрія Декартові координати на площині Відстань між точками Якщо , – довільні точки і AB відстань між ними, то або . У випадку, коли точка B збігається з початком координат , отримуємо: . Рівнянням фігури на площині в декартових координатах називається рівняння з двома змінними x і y, яке задовольняють координати будь-якої точки фігури й […]...
- Дотична до кола Урок № 43 Тема. Дотична до кола Мета: вивчити означення дотичної до кола, теореми про властивість та ознаку дотичної до кола. Сформувати вміння: – відтворювати формулювання означення, властивості та ознаки дотичної; – використовувати ці формулювання під час розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Дотична […]...
- Коло. Довжина кола Розділ 3 Відношення і пропорції §29. Коло. Довжина кола Дуже давно люди винайшли колесо та побачили його корисні в побуті властивості. Геометричними фігурами, які дають уявлення про колесо, є коло і круг. На малюнку 15 зображено креслярський інструмент – циркуль. На одній його ніжці – вістря, а на другій – грифель. Якщо поставити ніжку з […]...
- Довжина кола Геометрія Многокутники Довжина кола Теорема. Відношення довжини кола до його діаметра не залежить від кола, тобто є одним і тим самим числом для будь-яких двох кіл. Це число позначається . , де l – довжина кола, R – радіус. Отже, або ; – число ірраціональне, . Довжина дуги кола, яка відповідає центральному куту : . […]...
- Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Координати середини відрізка Геометрія Декартові координати на площині Координати середини відрізка Якщо , – довільні точки, – середина відрізка AB, то ; ....
- КОЛО, КРУГ ТА ЇХ ЕЛЕМЕНТИ. ЦЕНТР КОЛА (круга), РАДІУС, ДІАМЕТР. ПОБУДОВА КОЛА. РОЗВ’ЯЗУВАННЯ ВПРАВ І ЗАДАЧ НА ВИВЧЕНІ ВИПАДКИ АРИФМЕТИЧНИХ ДІЙ АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ ТА ДІЛЕННЯ (продовження) Урок 68. КОЛО, КРУГ ТА ЇХ ЕЛЕМЕНТИ. ЦЕНТР КОЛА (круга), РАДІУС, ДІАМЕТР. ПОБУДОВА КОЛА. РОЗВ’ЯЗУВАННЯ ВПРАВ І ЗАДАЧ НА ВИВЧЕНІ ВИПАДКИ АРИФМЕТИЧНИХ ДІЙ Мета: ознайомити учнів із кругом і колом; навчати відрізняти круг і коло; вчити працювати з циркулем; формувати вміння розв’язувати приклади і задачі на вивчені випадки арифметичних […]...
- Складніші задачі на побудову Розділ 1. Найпростіші геометричні фігури та їх властивості § 19. Складніші задачі на побудову 736. Так. 737. Мал. 401. X належить бісектрисі кута В та колу. Мал. 402. X належить бісектрисі кута В та серединному перпендикуляру ОХ до відрізка ВС. Мал. 403. X належить серединному перпендикуляру ВО до відрізка АС та колу. 738. 1) Спочатку […]...
- Описані і вписані кола Розділ 1. Найпростіші геометричні фігури та їх властивості § 17. Описані і вписані кола 671. Коло, описане навколо трикутника, зображено на мал. 372. 672. Коло, вписане у трикутник, зображено на мал. 375. 673. Центр кола, описаного навколо гострокутного трикутника, лежить всередині трикутника. Центр кола, описаного навколо прямокутного трикутника, лежить на середині гіпотенузи. Центр кола, описаного […]...
- Довжина кола і дуги кола УРОК № 20 Тема. Довжина кола і дуги кола Мета уроку: виведення формул для знаходження довжини кола та довжини дуги кола. Формування вмінь учнів застосовувати виведені формули до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Довжина кола і площа круга” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють формули довжини кола і […]...
- Графік рівняння з двома змінними УРОК № 28 Тема. Графік рівняння з двома змінними Мета уроку: домогтися засвоєння учнями змісту: означення графіка рівняння з двома змінними; схеми дій для побудови графіка рівняння з двома змінними. Виробити вміння: відтворювати зміст вивченого означення та алгоритму; застосовувати їх для розв’язування вправ на побудову графіків рівнянь з двома змінними. Тип уроку: узагальнення та систематизація […]...
- Системи рівнянь – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Лінійне рівняння з однією змінною – рівняння, що зводиться до канонічного вигляду ах + b = 0, де х – змінна, а й b – константи. Корінь рівняння ах + b = 0 визначається формулою: х = – b/а – якщо а ≠ 0, множина розв’язків L = {-b/a}. – […]...
- Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Візьмемо три взаємно перпендикулярні прямі Oх, Oy, Oz, які перетинаються в одній точці О (див. рисунок). Проведемо через кожну пару цих прямих площину. Площина, яка проходить через прямі Oх і Oу, називається площиною Oxy. Дві інші площини називаються відповідно Oxz і Oyz. Прямі Ox, Oy, Oz називаються Координатними […]...
- Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...
- Дуга кола й круговий сектор – КОЛО Формули й таблиці МАТЕМАТИКА КОЛО Р – пряма, що не має спільних точок з колом T – дотична К – радіус D – діаметр G – січна S – хорда С – довжина кола Дотична й радіус, проведений у точку дотику, перпендикулярні. B – дуга кола α – кут між дотичною і хордою β – […]...
- Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...
- Довжина кола. Число n Урок № 5 6 Тема. Довжина кола. Число n Мета: повторити відомості, які учні мають з початкової школи про коло; сформувати більш строге геометричне уявлення про коло, його елементи та співвідношення між ними; дати зміст поняття “довжина” кола і виробити вміння знаходити довжину кола за відомим радіусом або діаметром та розв’язувати обернену задачу. Тип уроку: […]...
- Властивості сфери і кулі 1. Відстань, яка б відділяла мене від мого антипода дорівнювала б Двом радіусам Землі. Відповідь: 2R Землі. 2. Нехай АО – радіус Землі, ОА = 6400 км, О1А – радіус Полярного кола Землі. Координати Полярного кола Землі 66°31′ п. ш. ∠АОВ = 66°31′; ∠О1ОА = 90° – 67° = 23°. З ΔO1ОA: Ο1Α = ОА […]...
- РІВНЯННЯ СТАНУ ІДЕАЛЬНОГО ГАЗУ (РІВНЯННЯ КЛАПЕЙРОНА – МЕНДЕЛЄЄВА) – ВЛАСТИВОСТІ ГАЗІВ (ГАЗОВІ ЗАКОНИ) Фізика підготовка до ЗНО комплексне видання МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА 2. ВЛАСТИВОСТІ ГАЗІВ (ГАЗОВІ ЗАКОНИ) – Не зберігають ні форми, ні об’єму. – Характер молекулярного руху: безладний (хаотичний) рух. 2.1. РІВНЯННЯ СТАНУ ІДЕАЛЬНОГО ГАЗУ (РІВНЯННЯ КЛАПЕЙРОНА – МЕНДЕЛЄЄВА) Рівняння стану ідеального газу зв’язує макроскопічні параметри р, V, Т, які характеризують стан даної маси тіла. Рівняння […]...
- ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &22. ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що кожній упорядкованій парі чисел відповідає певна точка на координатній площині. Оскільки кожний розв’язок рівняння з двома змінними х і у – це упорядкована пара чисел, то всі його розв’язки можна зобразити точками па координатній площині. У цих точок […]...
- Найпростіші задачі па побудову Розділ 1. Найпростіші геометричні фігури та їх властивості § 18. Найпростіші задачі па побудову 708. Щоб побудувати трикутник, що дорівнює трикутнику ABC, треба провести три кола радіусами 5 см, 6 см і 9 см. 709. 710. 1) AС = 5 см; 2) AС = 0,35 дм; 3) AС = 43 мм. 711. 1) Будуємо відрізок […]...