Розкладання багаточленів на множники способом групування
Урок № 40
Тема. Розкладання багаточленів на множники способом групування
Мета: вдосконалити вміння та відпрацювати навички розкладання багаточленів на множники способом групування та використання цього перетворення многочленів для розв’язування різноманітних завдань.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
І. Перевірка домашнього завдання
@ Оскільки № 1 та 2 домашнього завдання були вправами на закріплення вироблених умінь, виконання цих вправ перевіряємо вибірково (у слабких учнів) під час перевірки.
Фронтально
1. Який з наведених виразів є правильним розкладом багаточлена
Mа – nа + mb – nb на множники:
1) а(m – n) + b(m – n);
2) (m – n)(а + b);
3) (mа – nа) + (mb – nb)?
2. В якій з відповідей правильно вказано добуток, що утворився під час розкладання багаточлена 5a – bx – 5b + ax на множники способом групування:
1) (5а – bх) – (5b – ах);
2) 5(а – b) + х(а – b);
3) (а – b)(5 + х)?
По виконанні цього завдання: 1) перевіряємо (самоперевірка за готовим правильним розв’язанням, записаним на дошці);
II. Робота з випереджальним домашнім завданням
@ Перевіряємо відповіді домашнього завдання № 3, виправляємо помилки й порівнюємо та узагальнюємо висновки, зроблені учнями: розкладання багаточленів на множники (способом групування) може бути одним із засобів спрощення обчислень значень виразів.
III. Мотивація навчальної діяльності
1. Розв’яжіть рівняння х7 – 2х – х + 2 = 0
Запитання для осмислення змісту завдання
– Чи є дане рівняння лінійним?
– Чи можна розв’язати це рівняння шляхом рівносильних перетворень?
– Як можна перетворити ліву частину рівняння?
– Яку властивість множення Можна при цьому використати?
2. Обчисліть значення виразу найбільш раціональним способом: 17,2 • 8,1 + 23,8 • 5,1 – 17,2 • 7,6 – 23,8 • 4,6.
Запитання для осмислення змісту завдання
– Яку послідовність виконання дій закладено в умові задачі?
– Чи буде такий спосіб обчислень раціональним?
– Чи можна перетворити дану алгебраїчну суму в добуток? Яким способом?
Висновки. Для розв’язування деяких задач необхідно розкласти вираз, даний в умові, на множники, в тому числі за алгоритмом розкладання багаточлена на множники способом групування.
IV. Удосконалення вмінь. Відпрацювання навичок
Виконання письмових вправ
1. Розв’яжіть рівняння/розклавши на множники ліву частину рівняння:
1) х2 + 2х + 3х + 6 = 0;
2) х2 – 2х – х + 2 = 0;
3) х2 – 4х – х + 4 = 0;
4) х2 + 3х – 2х – 6 = 0.
2. Знайдіть значення виразу найбільш раціональним способом:
1) 17,2 • 8,1 + 23,8 • 5,1 – 17,2 • 7,6 – 23,8 • 4,6;
2) 
.
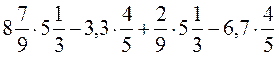3. Обчисліть значення виразу, попередньо розклавши його на множники:
1) 8а2 – 8аb – 5а + 5b якщо а =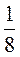 
, b = –
;
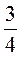2) 10у3 + у2 +10у + 1, якщо у = 0,3.
4*. Розкладіть на множники тричлен, подавши попередньо один з його членів у вигляді алгебраїчної суми подібних доданків:
1) х2 + 5х + 6; 2) х2 – 5х + 4; 3) х2 + х – 6; 4) х2 – 4х + 3.
@ Первинне сприйняття алгоритму роботи з подібними завданнями для учнів складне, тому бажано, щоб учні порівняли запропоновані в цій вправі завдання із кількома розв’язаними попередньо (див. № 1) та змістовно попрацювали з алгоритмом, а саме: Скільки членів треба мати в багаточлені, щоб можна було застосувати спосіб групування? Скільки членів є в даних багаточленах?
Порівняйте багаточлени кожної пари:
1) х2 – 3х + 2 та х2 – 2х – х + 2;
2) х2 + 5х + 6 та х2 + 2х + 3х + 6;
3) х2 + х – 6 та х2 + 3х – 2х – 6;
4) х2 – 5х + 4 та х2 – 4х – х + 4.
Зробіть висновки. На основі цих висновків розкладіть на множники дані вирази.
5*. Доведіть тотожність;
1) (х + а)(х + b) = х2 + (а + b)х + аb; 2)(х – а)(х – b) = х2 – (а + b)х + аb,
Де a, b – числа.
@ У розв’язуванні № 4 і 5 можливий інший порядок: спочатку учні доводять відповідні тотожності (№ 5*), а потім використовують ці тотожності для розкладання тричленів на множники.
V. Підсумки уроку
Види завдань на застосування алгоритму розкладання багаточленів на множники способом групування:
1) розкласти на множники багаточлени;
2) обчислити раціональним способом (числові та буквені вирази);
3) розв’язати рівняння.
VI. Домашнє завдання
Виконайте завдання. Ті, що викликали труднощі, виділіть.
№ 1. Домашня самостійна робота.
Варіант 1 | Варіант 2 |
1. Розкладіть на множники: | |
1) ха + хb + 6а + 6b; 2) х3 – х2 + х – 1; | 1) ас + bс + 2а + 2b; 2) а3 – 2а2 + а – 2; |
3) ab – 2a – 2b + 4; 4) x5 + 2×4 – х – 2; | 3) 3х + 9 – ху – 3у; 4) х4 + 3х3 – х – 3; |
5) ab – ac – a2 + bс | 5) ху – а2 – ах + ау |
2. Розв’яжіть рівняння: | |
Х2 + 8х + 7 = 0 | Х2 + 6х + 8 = 0 |
№ 2. Випереджальне домашнє завдання. За підручником систематизувати знання, набуті з теми “Багаточлени”, а саме:
1) виписати основні поняття теми;
2) які дії з багаточленами та за якими алгоритмами навчилися виконувати;
3) які приклади з підручника не с зрозумілими?
(1 votes, average: 5.00 out of 5)
Loading...