Розкладання многочленів на множники
702. Перетворити його в добуток кількох виразів.
703. 1) ні; 2) ні; 3) так.
704. 1) ні; 2) так; 3) ні.
705. 1) ні; 2) ні; 3) так.
706. 1) ні; 2) ні; 3) так.
707. ні; 2) так; 3) ні.
708. ні; 2) ні; 3) так.
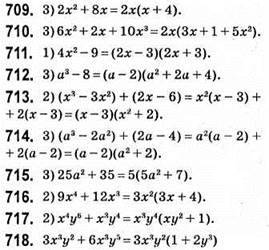
Жодна з рівностей не є тотожністю.
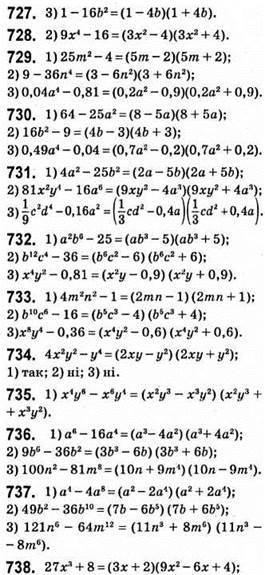
1) ні, не потрібен подвоєний добуток;
2) так;
3) ні, знаки в дужках невірно записані.
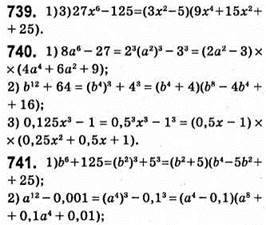
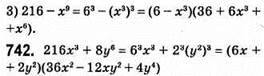
1) У других дужках не потрібен подвійний добуток;
2) все вірно;
3) у других дужках 6 і 2
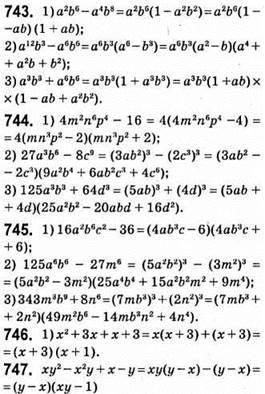
1) помилка в перших дужках – змінити знаки;
2) все вірно;
3) у перших дужках перед х потрібно поставити знак “-“.
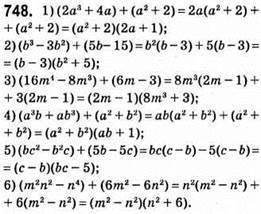
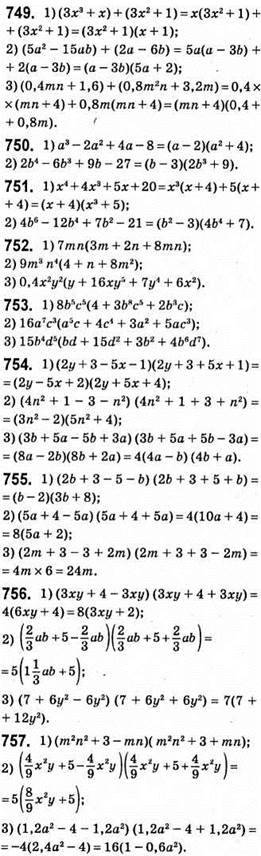
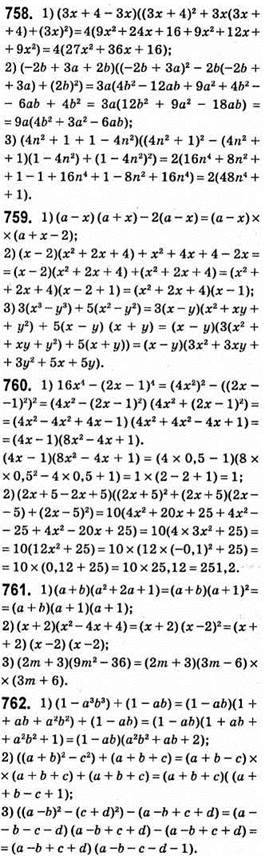
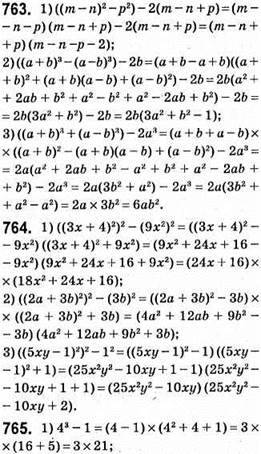
3 • 21 : 7 = 3 • 3 = 9, тобто 43 – 1 ділиться на 7;
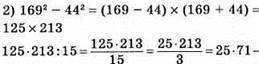ціле число;
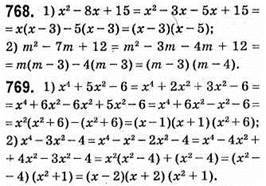
770. 1) x2 – 16 = 0; (x – 4)(x + 4) = 0; x – 4 = 0 або x + 4 = 0; x = 4 або x = -4;
2) (2x – 1)2 – 52 = 0;
(2x – 1 – 5)(2x – 1 + 5) = 0;
(2x – 6)(2x + 4) = 0;
2x – 6 = 0; 2x = 6; x = 6 : 2; x = 3 або 2x + 4 = 0;
2x
3) x2 – 9 – 6x – x2 – 3x = 0;
-9 – 9x = 0; -9x = 9; x = 9 : (-9); x = -1.
При n = 1 маємо, що 4 • 0 поділиться на 6; при n = 2 маємо, що 5 • 6 ділиться на 6, бо один із множників ділиться на 6.
Нехай виконується для будь-якого n, тоді повинно виконуватися і для n + 1:
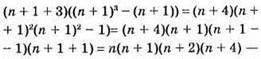
Для будь-якого n вираз ділиться на 6.
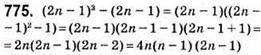
При n = 1 буде 0, а 0 ділиться на будь-яке число;
При n = 2 : 8 • 1 • 3 = 24 ділиться на 24;
При n = 3 : 12 • 2 • 5 : 24 = 5, також ділиться на 24;
При n = 4 : 16 • 3 • 7 = 48 • 7 ділиться на 24, в результаті отримаємо 14.
Нехай виконується для n = k, тоді і для n = k + 1 також буде виконуватися:
(2(k + 1) – 1)3 – (2(k + 1) – 1) = 4(k + 1) • (k + 1 – 1)(2k + 2 – 1) = 4(k + 1)k(2k + 1), при k ≥ 0 для будь-якого k ≥ 0: 4(k + 1) • k(2k + 1) поділиться на 24, а значить і вираз (2n – 1)3 – (2n – 1) ділиться на 24 за математичною індукцією.
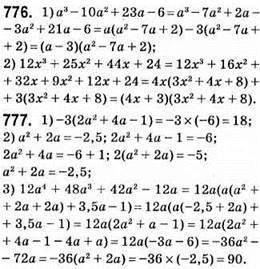
Застосуйте на практиці
778. а2 – площа підлоги першої кімнати; b2 – площа підлоги другої кімнати; 2аb – подвоєна площа підлоги третьої кімнати;
A2 + b2 + 2ab = 49; (а + b)2= 49; а + b = 7.
Р = 2(а + b) = 2 • 7 = 14 (м) – периметр кімнати, що має форму прямокутника.
779. Нехай x – вік тата; у – вік доньки, тоді x2 – у2 = 25 • 49;
(x – у)(х + у) = 25 • 49; x – у = 25, а (x + у) = 49, тоді маємо, що у = 12, а x = 37.
12 років доньці і 37 років татові.
Задачі на повторення
780. 1) |5x – 2| = 8
5x – 2 = 8; 5x = 8 + 2; 5x = 10; x = 2 або 5x – 2 = -8; 5x = -8 + 2; 5x = -6;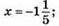 
2) а) при х > 0: 2х + 3х – 3 = 5; 5x = 8;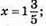 
Б) при x < 0: -2x + 3x – 3 = 5; x = 8 – не підходить;
В) при x = 0: 2 • 0 + 3 • (0 – 1) = 5;
-3 = 5 – невірно, тобто x = 0 – не підходить.
Відповідь: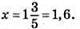 
781. Нехай друге число x, тоді перше – 1,4x, їх середнє арифметичне: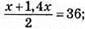 
2,4x = 72; x = 30 – друге число; 1,4 • 30 = 42 – перше число.
(1 votes, average: 5.00 out of 5)
Loading...