Головна ⇒ 📌Математика ⇒ Розв’язування вправ на всі дії з раціональними числами

Розв’язування вправ на всі дії з раціональними числами

Розділ 4 Раціональні числа і дії мідними

§50. Розв’язування вправ на всі дії з раціональними числами

1414. (Усно) Обчисли:

1) 5 + (-3); 2) -3 + (-8); 3) 4 – 7;

4) -2 – (-4); 5) -5,3 ∙ (-10); 6) -4,2 ∙ 0,1;

7) 4,7 : (-10); 8) -8,3 : (-0,1).

1415. (Усно) Обчисли:

1) 9 + (-9) + 10; 2) -8 + (-7) + 8;

3) -2 ∙ 50 ∙ (-8); 4) 4 ∙ (-17) ∙ 0.

1416. Знайди значення виразу:

1) -5,3 + (-4,9); 2) -2,9 + 1,3; 3) 0 – 7;

4) 14,2 – (-1); 5) 21 ∙ (-13); 6) -12 ∙ (-14);

7) -1,8 : (-2); 8) -2,5 : 0,5.

1417. Обчисли:

1) -4,7 + 5,9; 2) -2,7 + (-3,8); 3) 1 – 8;

4) -3 – (-2); 5) -14 ∙ 18; 6) -25 ∙ (-16);

7) -1,6 : 4; 8) -5,7 : (-0,3).

1418. (Усно) Спрости:

1) 3p – 2p; 2) 4x –

5x; 3) -2y + 5y;

4) -3y – y; 5) m – m; 6) -2p + p.

1419. (Усно) Знайди корінь рівняння:

1) х + 3 = 2; 2) х – 3 = -5;

3) х ∙ (-7) = 21; 4) х : (-4) = -5.

1420. Знайди значення виразу:

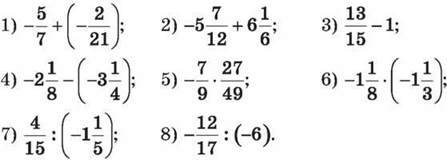
1421. Обчисли:

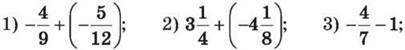
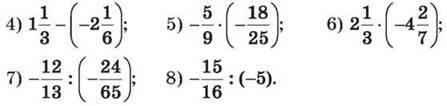
1422. Знайди середнє арифметичне чисел:

1) 12,5; -13,8; -5,3; 2) 12,7; -2,5; -14,1; 3,5.

1423. Знайди середнє арифметичне чисел:

1) 7,8; -13,6; 2) -2,5; 3,7; 4,9; -5,6; -8.

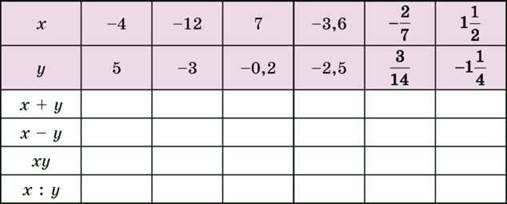
1424. Заповни в зошиті таку таблицю:

1425. Обчисли, потім заповни таблички відповідними буквами та прочитай ім’я та прізвище видатного українського письменника:

1) -4,5 + (-2,7) = Р; 2) -2,7 + 3,8

= В;

3) -5,2 – 4,7 = І; 4) 5,2 – (-2,5) = О;

5) -1,2 ∙ 4,5 = А; 6) -1,8 ∙ (-5,5) = К;

7) -8,1 : (-1,8) = Н; 8) 8,5 : (-2,5) = Ф.

1426. Обчисли, потім заповни таблички відповідними буквами та прочитай прізвище видатного українського математика:

1) -2,7 + (-3,8) = А; 2) 4,9 – 5,8 = У;

3) -2,7 – (-3,6) = К; 4) 3,6 ∙ (-1,5) = Ч;

5) -8 ∙ (-4,7) = В; 6) -12 : 2,5 = Р.

1427. Обчисли значення виразу 29,4 – а : b, якщо:

1) а = -33,5; b = 2,5; 2) а = -32,16; b = -2,4.

1428. Обчисли значення виразу x : y – 23,7, якщо:

1) x = -3,3; y = 1,2; 2) x = -7,12; y = -4,45.

1429. Заповни в зошиті таку таблицю:

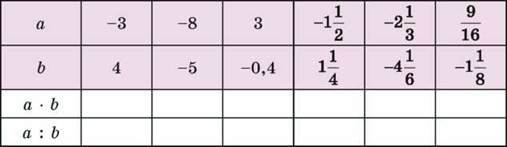
1430. Заповни в зошиті таку таблицю:

1431. Обчисли:

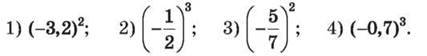
1432. Обчисли:

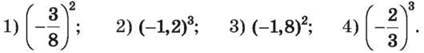
1433. Розв’яжи рівняння:

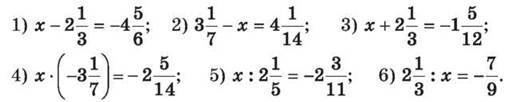
1434. Розв’яжи рівняння:

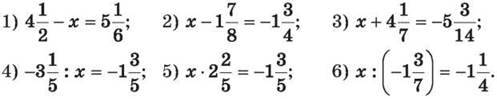
1435. Що більше: сума чисел 0,5 і -3,2 чи їх добуток? На скільки?

1436. На скільки сума чисел -7,2 і -6,4 менша від їх частки?

1437. На скільки частка чисел -5,75 і 2,3 більша за їх суму?

1438. Розв’яжи рівняння:

1) 0,4(3 – 2x) + 2,4 = 0,2(3 + 2x);

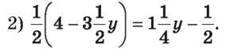
1439. Розв’яжи рівняння:

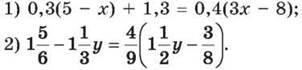
1440. Виконай дії:

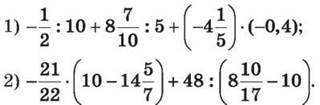
1441. Виконай дії

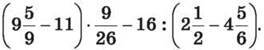
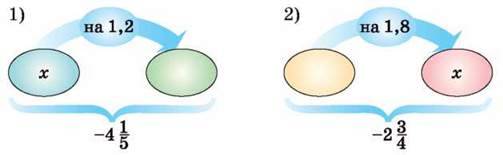
1442. Склади рівняння за схемою та розв’яжи його (стрілка напрямлена до більшого числа):

1443. Знайди суму чотирьох чисел, перше з яких дорівнює -4,7, а кожне наступне на 1,8 більше за попереднє.

1444. Знайди суму чотирьох чисел, перше з яких дорівнює 2,7, а кожне наступне на 1,6 менше від попереднього.

1445. (Усно) Доведи, що коли x Ф 0, y Ф 0, то значення виразів xy та має один і той самий знак.

1446. Обчисли, використовуючи розподільну властивість множення:

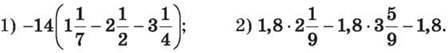
1447. Обчисли, використовуючи розподільну властивість множення:

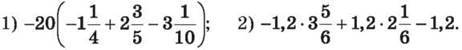
1448. Розв’яжи рівняння:

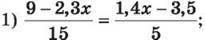
2) 0,25(3x – 4) = 0,45(4x – 2) – 2,2. 1449. Розв’яжи рівняння:

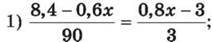
2) 0,2(х – 3) – 0,58 = 0,35(6x – 5).

1450. Доведи, що значення виразу 3(13 – 2x) – 4(x – 8) + 5(2x + 8) не залежить від значення змінної.

1451. Доведи, що значення виразу -2(3y – 5) + 7(5 – 2y) + 10(2y – 8) не залежить від значення змінної.

1452. Виконай дії

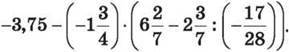
1453. Виконай дії

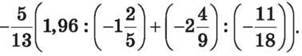
1454. Спрости вираз 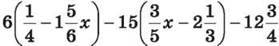та знайди його значення, якщо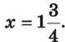

1455. Спрости вираз 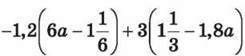та знайди його значення, якщо а = -5.

1456. Обчисли:

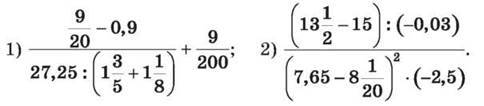
1457. Обчисли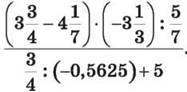

1458. Накресли координатну пряму, взявши за одиничний відрізок п’ять клітинок зошита. Познач на ній точки А(-0,6); В(2,4),

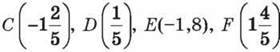
1459. Чи можна, використовуючи лише цифри 2 і 3, записати деяке натуральне число, кратне:

1)2; 2) 5; 3) 10; 4) 3; 5) 9?

1460. Запиши у вигляді нескінченного десяткового періодичного дробу частку:

1) 2 : 9; 2) 7 : 11; 3) 13 : 12; 4) 100 : 99.

1461. Одну зі сторін прямокутника збільшили на 20 %, а другу – на 30 %, утворивши новий прямокутник. На скільки відсотків збільшилася площа прямокутника?

1462. Яке найбільше натуральне число можна записати за допомогою: 1) двох п’ятірок; 2) трьох двійок?