Розв’язування задач на додавання швидкостей
КІНЕМАТИКА
Урок № 5
Тема. Розв’язування задач на додавання швидкостей
Мета: виробляти вміння та навички учнів з використання правила додавання швидкостей; розвивати вміння обирати найбільш зручну систему відліку під час розв’язування задач, логічне мислення; виховувати самостійність, наполегливість, грамотність в оформленні задач.
Тип уроку: удосконалення знань та формування вмінь розв’язувати задачі.
Очікувані результати. Після уроку учні:
– вмітимуть розв’язувати задачі з використання правила додавання
ХІД УРОКУ
I. Перевірка домашнього завдання
– Оглядова перевірка зошитів з метою з’ясування наявності розв’язання учнями задач, які було задано додому.
– Фізичний диктант із взаємоперевіркою.
II. Розв’язування задач
Повідомлення теми та мети уроку, очікуваних результатів.
Розв’язування якісних задач
1. За якої умови льотчик реактивного винищувача може роздивитися артилерійський снаряд, що пролітає неподалік від нього?
2. Пасажир швидкого поїзда дивиться у вікно на вагони зустрічного потяга. У той момент, коли останній вагон зустрічного поїзда проїхав
3. Чому дощові краплини безвітряної погоди залишають скісні смуги на склі автомобіля, який рівномірно рухається?
4. Двоє плавців перепливають річку. Один пливе перпендикулярно до течії, другий – найкоротшим шляхом. Який із них переправиться на другий берег річки за найменший час, якщо модулі їхніх швидкостей відносно води є однаковими?
5. Заважає чи допомагає течія перепливти річку за найкоротший час? найкоротшим шляхом? Вважайте, що ширина річки та швидкість течії є скрізь однаковими.
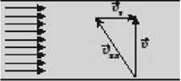
Розв’язання. Якщо тримати курс під прямим кутом до берега (тобто якщо швидкість плавця відносно води напрямлена перпендикулярно до берега), то плавця буде зносити вниз за течією. Оскільки течія не наближає плавця до протилежного берега і не віддаляє від нього, найкоротший час переправи не залежить від швидкості течії. А от для переправи найкоротшим шляхом слід тримати курс угору за течією, щоб швидкість відносно берега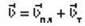 
була перпендикулярною до берега. Оскільки 
< Пл (див. рисунок), течія заважає перепливти річку найкоротшим шляхом. Якщо Пл < Т, то така переправа неможлива.
Розв’язування розрахункових задач
1. Пасажир поїзда помітив, що дві зустрічні електрички промчали повз нього з інтервалом t1 = 6 хв. З яким інтервалом часу t2 проїхали ці електрички повз станцію, якщо поїзд, на якому перебуває пасажир, рухався зі швидкістю 1 = 100 км/год., а швидкість кожної з електричок 2 = 60 км/год.?
Розв’язання. Знайдемо відстань між електричками у двох системах відліку – у системі відліку “поїзд”, зв’язаній із пасажиром, і в системі відліку, зв’язаній зі станцією. У системі відліку “поїзд” електрички рухаються зі швидкістю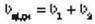 
. Оскільки вони проходять повз пасажира з інтервалом часу t1, відстань між електричками дорівнює 
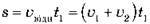. У системі ж відліку, пов’язаній зі станцією, 
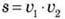. Прирівнюючи два вирази для s, одержуємо: 
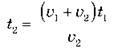. Підставляючи числові дані, знаходимо t2 = 16 хв.
2. Ескалатор підіймає людину, яка стоїть на ньому, за t1 = 1 хв., а якщо людина йде вгору зупиненим ескалатором, на підняття витрачається t2 = 3 хв. Скільки часу знадобиться на підняття, якщо людина йтиме вгору по ескалатору, який рухається вгору?
III. Виконання самостійної роботи “Додавання переміщень і швидкостей, перехід в інші системи відліку”
Початковий рівень
1. З полиці вагона, що рівномірно рухається, падає яблуко. Якою є траєкторія руху яблука відносно спостерігача, який стоїть на пероні? Зобразіть траєкторію на рисунку.
2. Корабель підходить до пристані. Відносно яких тіл пасажири, які стоять на палубі цього корабля, перебувають у русі: а) річки; б) палуби корабля; в) берега?
Середній рівень
1. Два поїзди рухаються в одному напрямі зі швидкостями 70 і 50 км/год. відносно землі. Визначте: а) модуль швидкості першого поїзда відносно другого; б) модуль швидкості другого поїзда відносно першого.
2. Швидкість першого автомобіля відносно другого 30 км/год., а відносно землі – 120 км/год. Визначте модуль швидкості другого автомобіля відносно землі, якщо автомобілі рухаються в одному напрямі.
IV. Домашнє завдання
1. Повторити відповідний параграф підручника.
2. Розв’язати задачі.
– Зустрічні поїзди однакової довжини проходять один повз одного. Пасажир першого поїзда помітив, що другий поїзд пройшов повз за 20 с. За який час повз пасажира другого поїзда пройшов перший, якщо швидкості поїздів 40 і 60 км/год.?
– Катер перетинає річку шириною 1 км. Швидкість катера відносно води напрямлена перпендикулярно до берега, її модуль 4 м/с. На яку відстань течія знесе катер за час переправи, якщо швидкість течії дорівнює 1 м/с? Який шлях пройде катер?
(1 votes, average: 5.00 out of 5)
Loading...