Розв’язування задач за допомогою системи лінійних рівнянь
Урок № 80
Тема. Розв’язування задач за допомогою системи лінійних рівнянь
Мета: відпрацювати навички застосування схеми розв’язання текстових задач на складання системи лінійних рівнянь із двома змінними до розв’язування задач на рух; вдосконалювати вміння розв’язувати системи лінійних рівнянь із двома змінними аналітичними способами.
Тип уроку: застосування знань, умінь та навичок.
Хід уроку
I. Організаційний момент (традиційно)
II. Перевірка домашнього завдання
@ Для пожвавлення процесу пропонуємо
Самостійна робота
Розв’яжіть задачу, склавши систему рівнянь.
Удвох шафах стояли книжки. Якщо з першої шафи переставити у другу 10 книжок, то в обох шафах книжок стане порівну. Якщо із другої шафи переставити в першу 44 книги, то в ній залишиться в 4 рази менше книжок, ніж у першій. Скільки книжок було в кожній шафі?
(По закінченні розв’язування учні за бажанням здають роботи, оцінюємо найкращі, всі інші здійснюють самоперевірку за зразком.)
Під час виконання самостійної роботи можна запропонувати більш слабким
III. Формулювання мети й завдань уроку
Нагадуємо учням про існування і необхідність розгляду ще одного виду задач – на рух. Тому основна навчальна мета уроку: навчитися складати системи лінійних рівнянь, що відображають процес руху (прямолінійного, рівномірного), описаний в текстових задачах.
V. Актуалізація опорних знань
Виконання усних вправ
1. Розв’яжіть рівняння: 1)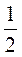 
Х – 3 = 0; 2) 
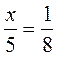; 3) 2х – 3 = 2; 4) 0х = 5.
2. Розв’яжіть систему рівнянь найзручнішим способом:
1) 
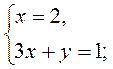2) 
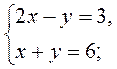3) 
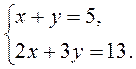
3. Складіть рівняння за умовою задачі:
1) сторони прямокутника х та у, а периметр 26 см;
2) в одній шафі х книжок, у другій у книжок; якщо перекласти з першої шафи у другу 20 книжок, то в першій буде у 2 рази більше, ніж стало у другій; зошит коштує х грн.., ручка у грн..; за дві ручки заплатили на 2 грн. більше, ніж за три зошити.
VI. Засвоєння вмінь. Розв’язування задач
@ На уроці ми розв’язуємо найбільш поширений вид текстових задач – задачі на рух (прямолінійний, рівномірний). Схема розв’язання цих задач така сама, як і в інших видах текстових задач. Єдине, що їх відрізняє,- це наявність певних співвідношень між величинами, що характеризують цей рух (S; v; t; v за теч; v проти теч; v власна та v течії), які потрібно знати і вміти використовувати для вираження одних через інші відповідно до умови задачі. Саме з цих співвідношень і бажано розпочати розмову про розв’язування задач на рух:
S = vt;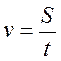 
; 
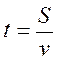; v за теч = v власна + vтечії; v проти теч = v власна – v течії.
Ще на один момент хотілося б звернути увагу: перед складанням системи рівнянь зручно записати коротку умову задачі у вигляді таблиці й подальшу роботу зі складання системи рівнянь проводити як роботу з таблицею.
V | T | S |
І вид руху | ||
II вид руху |
Виконання письмових вправ
1. Перший автомобіль долає шлях між двома містами за 2 год., а другий – за 2,5 год. Знайдіть швидкість кожного автомобіля, якщо за 1,5 год. перший з них проїжджає на 30 км більше, ніж другий.
2. З пункту А до пункту В, відстань між якими 41 км, вийшов турист. Через 1 год. назустріч йому з пункту В вийшов інший турист. Через дві години після виходу другого туриста відстань між ними була 18 км, а ще через 2 год. вони зустрілися. Знайдіть швидкість туристів.
3. Теплохід проходить за 2 год. за течією річки й за 3 год. проти течії 222 км. За 3 год. за течією він проходить на 60 км більше, ніж за 2 год. проти течії. Знайдіть швидкість теплохода в стоячій воді та швидкість течії річки.
4. (На повторення). Сума двох чисел дорівнює 24. Зайдіть ці числа, якщо 35 % одного з них дорівнює 85 % іншого.
VII. Підсумок уроку
Узагальнюємо та систематизуємо уявлення про: 1) зміст задач на складання систем рівнянь із двома змінними та 2) загальну схему розв’язання таких задач складанням системи рівнянь.
VIII. Домашнє завдання
№ 1. Випишіть основні поняття теми. Повторіть зміст цих понять.
№ 2. Розв’яжіть задачі, використовуючи схему розв’язання задач складанням системи рівнянь. Для розв’язування складних систем доберіть найбільш раціональний спосіб:
1) Два туристи вирушили одночасно з двох міст, відстань між якими 38 км, і зустрілись через 4’год. З якою швидкістю рухався кожний турист, якщо відомо, що перший до зустрічі подолав на 2 км більше за другого?
2) За 3 год. за течією і 4 год. проти течії теплохід долає 380 км. За 1 год. за течією та 30 хв. проти течії теплохід долає 85 км. Відшукайте власну швидкість теплохода та швидкість течії.
(1 votes, average: 5.00 out of 5)
Loading...