Середнє арифметичне, середнє значення величин
Урок 113
Тема. Середнє арифметичне, середнє значення величин
Мета: систематизувати знання учнів щодо понять “середнє арифметичне”, сформувати вміння учнів розв’язувати задачі високого рівня складності на застосування цих понять.
Тип уроку: узагальнення і систематизація навичок, знань і вмінь.
Хід уроку
I. Розминка
Усні вправи
1. Обчисліть:
1) 0,5 – 2,5 – 4 – 2;
2) 2 – 1,69 – 500;
3) 8,6 – 0,34 + 1,4 – 0,34;
4) 10,8 – 11,3 – 10,8 – 10,9.
2. Знайдіть значення виразу 6,5а + 0,035b, якщо:
1) а = 10; b = 1000;
2) a
3) a = 0,1; b = 0;
4) a = 0; b = 0,2.
II. Перевірка домашнього завдання
Чи правильно записано вирази до розв’язання домашніх вправ № 1002 і 1008?
№ 1002.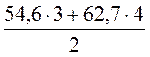 
.
№ 1008. Якщо х грн. – ціна цукерок третього виду, то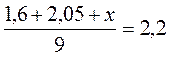 
?
@ Незважаючи на те, що вдома учні розв’язують ці задачі за діями, але якщо в них є розуміння суті розв’язування задач на знаходження середніх величин, то легко знаходять помилки у відповідних записах. (№ 1002 – знаменник дорівнює 7; № 1008 – у чисельнику не вистачає множників біля кожного з додатків – кількості кілограмів цукерок кожного виду:
1,6
ІІІ. Узагальнення знань
Запитання до класу
1. Сума 6 чисел дорівнює 45. Чому дорівнює їх середнє арифметичне?
2. Змішали 4,сорти цукерок за ціною 7,5 грн.; 8,4 грн., 9,5 грн., 10,6 грн. Скільки коштує 1 кг суміші, якщо взяли:
1) кожного сорту цукерок по 1 кг;
2) цукерок 1 і 3 сорту – по 2 кг; цукерок 2 і 4 сорту – по 1 кг?
3. Чи може середнє арифметичне двох десяткових дробів бути натуральним числом? Якщо так – навести приклад.
IV. Розв’язування задач
@ Коментар. Оскільки поняття середнього арифметичного чисел і середньої величини (опрацьовані) осмислені учнями, на уроці розглядаються задачі високого рівня складності, розв’язання яких вимагає застосування понять про середнє арифметичне і середньою величину.
№№ 1005; 1010; 1012.
Розв’язання
№ 1005. Нехай х – менше число, тоді 4х – більше число, їх середнє арифметичне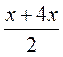 
дорівнює 10.
Складемо рівняння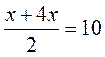 
, 
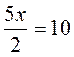, 5х = 20, х = 4.
Менше число 4, а більше 4 – 4 = 16.
Відповідь. 4 і 16.
№ 1010. Якщо середнє арифметичне перших чотирьох чисел дорівнює 2,1, то сума всіх чотирьох чисел 2,1 – 4 = 8,4.
Якщо середнє арифметичне другої трійки чисел 2,8, то їх сума 2,8 – 3 = 8,4.
Середнє арифметичне всіх семи чисел дорівнює їх сумі, поділеній на 7.
(8,4 + 8,4) : 7 = 16,8 : 7 = 2,4.
Відповідь. 2,4.
@ Перед розв’язуванням задачі вчитель може поставити запитання.
1. Що називається середнім арифметичним кількох чисел? Отже, що треба знати, щоб знайти середнє арифметичне чисел, зазначених у задачі?
2. Чи є значення виразу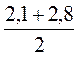 
значенням шуканої в задачі величини?
№ 1012. 1) Якщо середній вік одинадцяти гравців становить 22 роки, то сума всіх років 22 – 11 = 232 роки.
2) Якщо середній вік десяти гравців становить 21 рік, то сума всіх років 21 – 10 = 210 років.
3) Отже, вік футболіста, що залишив поле, 232 – 210 = 22 роки.
V. Підсумок уроку
Самостійна робота
Варіант 1 [2]
1. Знайдіть середнє арифметичне чисел: 32,6; 38,5; 34; 35;3 [26,3; 20,2; 24,7; 18]
2. Розв’яжіть задачу: Човен плив 2 год. зі швидкістю 12,3 км/год. і 4 год. зі швидкістю 13,2 км/год. Знайдіть середню швидкість човна упродовж усього шляху.
[Автомобіль їхав 3 год. зі швидкістю 62,6 км/год. і 2 год. зі швидкістю 65 км/год. Знайдіть середню швидкість автомобіля упродовж всього шляху.]
VI. Домашнє завдання
П. 33, №№ 1006; 1011; 1017.
(1 votes, average: 5.00 out of 5)
Loading...