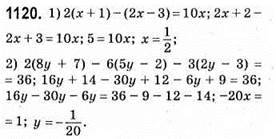Головна ⇒ 📌ГДЗ з математики ⇒ Система двох лінійних рівнянь із двома змінними
Система двох лінійних рівнянь із двома змінними
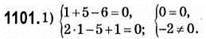
(1; 5) не є розв’язком системи, бо не задовольняє другому рівнянню;
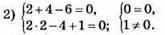
(2; 4) не є розв’язком системи, бо не задовольняє другому рівнянню.
1102. 1) мал. 80; (2; 1); 2) мал. 81: (2; 3); 3) мал. 82: (3; 3).
1103. 1) 1; 3; 5; 2) -3; 1; 4; 3) -3; 1; -5.
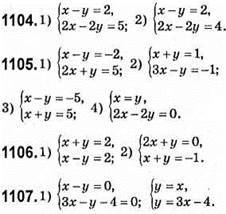
2 розв’язки до першого рівняння: (0; 0), (1; 1).
2 розв’язки для рівняння у = 3х – 4: (0; -4), (1; -1).
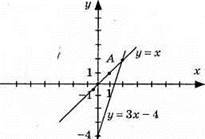
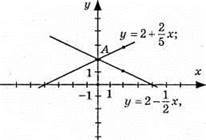
Графіки перетинаються в точці А(2; 2). Пара чисел (2; 2) є розв’язком системи.
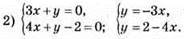
2 розв’язки
2 розв’язки для у = 2 – 4х: (0; 2), (1; -2).
Графіки перетинаються в точці А(2; -6). Пара чисел (2; -6) є розв’язком системи.
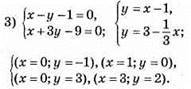
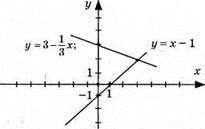
Пара чисел (3; 2) є розв’язком системи.
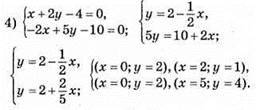
Графіки перетнулись в точці A(0; 2). Пара чисел (0; 2) є розв’язком системи.
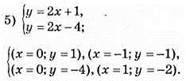
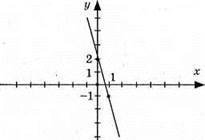
Графіки не перетинаються, значить, система не має розв’язку.
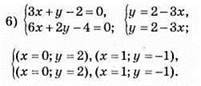
Графіки функцій співпадають,
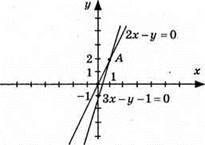
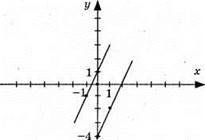
Графіки перетнулись в точці А(1; 2), пара чисел (1; 2) є розв’язком системи.
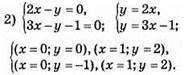
(дивись пункт 1).
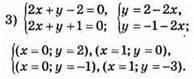
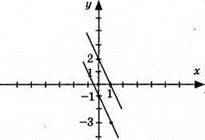
Графіки не перетинаються, система не має розв’язку.
4) дивись № 1107 (6).
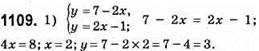
(2; 3) – точка перетину графіків.
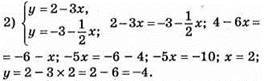
(2; -4) – точка перетину графіків.
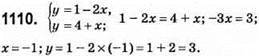
(-1; 3) – точка перетину графіків.
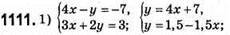
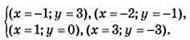
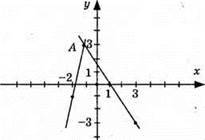
Графіки перетинаються в точці А(-1; 3), пара чисел (-1; 3) є розв’язком системи.
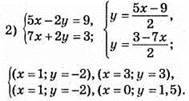
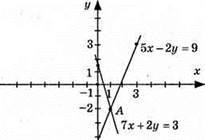
Графіки перетинаються вточці А(1; -2), пара чисел (1; -2) є розв’язком системи.
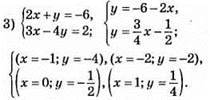
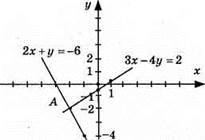
Графіки перетинаютьсявточці А(-2;-2), пара чисел (-2; -2) є розв’язком системи.
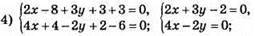
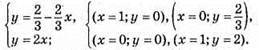
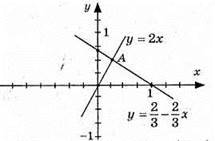
Графіки перетнулись в точці А(1/4; 1/2), пара чисел (1/4; 1/2) є розв’язком системи.
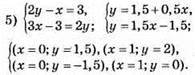
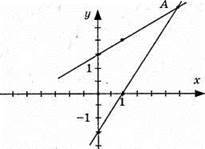
Графіки перетнулись в точці А(3; 3), пара чисел (3; 3) є розв’язком системи.
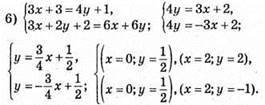
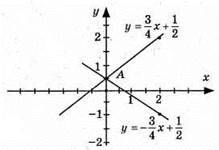
Графіки перетнулись в точці А(0; 1/2), пара чисел (0; 1/2) є розв’язком системи.
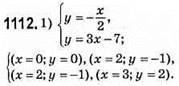
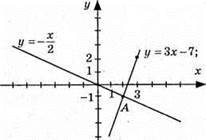
Графіки перетнулись в точці А(2; -1), пара чисел (2; -1) є розв’язком системи.
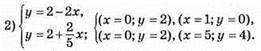
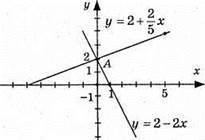
Графіки перетнулись в точці А(0; 2), пара чисел (0; 2) е розв’язком системи.
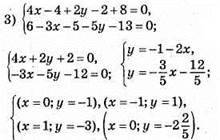
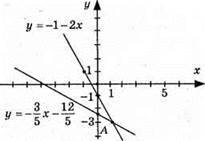
Графіки перетнулись в точці А(1; -3), пара чисел (1; -3) є розв’язком системи.
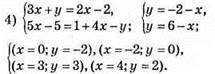
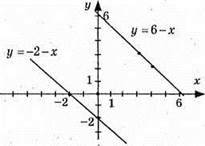
Графіки не перетинаються, значить, система не має розв’язків.
звідси -2 = а.
4; у = -2; у
1116. Якщо пара чисел (-2; 4) є розв’язком рівняння х + ау = 10, то ця пара задовольняє рівнянню: -2 + 4а = 10, звідси маємо 4а = 12; а = 3.
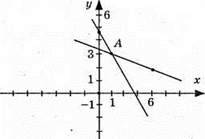
Графіки перетнулись в точці A(1; 3), пара чисел (1; 3) є розв’язком системи.
Застосуйте на практиці
1117. Нехай х грн коштує 1 зошит, а у грн коштує 1 ручка, тоді
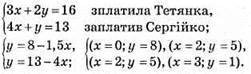
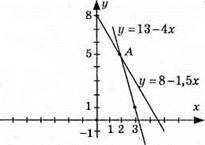
Графіки перетнулись в точці A(2; 5), пара чисел (2; 5) є розв’язком системи.
Задачі на повторення
1119. Нехай х км – весь шлях, тоді за 1-й день туристи пройшли 4/15x км, а за другий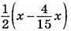 
км, а за третій – 11 км. Складаємо рівняння:
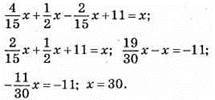
30 км подолали туристи за три дні.
(2 votes, average: 3.00 out of 5)
Loading...Related posts:
- Системи двох лінійних рівнянь із двома змінними А) х = 2; у = 1 – розв’язок системи, бо 2 – 2 • 1 = 0 – правильна рівність; 2 + 3 • 1 = 5 – правильна рівність; Б) x = 0; у = 0 – не є розв’язком системи, бо 0 – 2 • 0 = 0 – правильна рівність, а […]...
- Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 27. Система двох лінійних рівнянь з двома змінними та її розв’язок. Розв’язування систем лінійних рівнянь з двома змінними графічно Приклад 1. Маска й трубка для підводного плавання разом коштують 96 грн, причому маска на 16 грн дорожча за трубку. Скільки коштує маска і скільки трубка? Р о […]...
- Системи рівнянь із двома змінними. Графічний метод розв’язання систем двох лінійних рівнянь із двома змінними 1007. Розв’язком системи рівнянь є пара чисел (6; 4), бо – правильні рівності. 1008. Пара чисел (-5; 2) є розв’язком системи рівнянь бо – правильні рівності. 1009. а) (1; 4) _ розв’язок системи рівнянь, бо 1 + 4 = 5 – правильна рівність; 3 • 1 + 4 = 7 – правильна рівність. Б) (-1; […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &23. СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, як розв’язати задачу за допомогою лінійного рівняння з однією змінною. За допомогою лінійних рівнянь із двома змінними також можна розв’язувати задачі. Розглянемо приклад. Задача 1. Сума двох чисел дорівнює 3, а різниця подвоєного першого числа і потроєного […]...
- Система двох лінійних рівнянь із двома змінними та її розв’язок Урок № 72 Тема. Система двох лінійних рівнянь із двома змінними та її розв’язок Мета: сформувати уявлення учнів про розв’язок системи рівнянь із двома змінними та графічний спосіб розв’язання систем лінійних рівнянь; виробити вміння: здійснювати перевірку, чи є пара (х; у) розв’язком даної системи лінійних рівнянь; використовуючи навички побудови графіка лінійного рівняння з двома змінними, […]...
- СИСТЕМА ДВОХ ЛІНІЙНИХ РІВНЯНЬ З ДВОМА ЗМІННИМИ. ГРАФІЧНИЙ СПОСІБ РОЗВ’ЯЗАННЯ СИСТЕМ Цілі: – навчальна: сформувати поняття системи двох лінійних рівнянь з двома змінними, розв’язку системи двох лінійних рівнянь з двома змінними; сформувати вміння розв’язувати системи рівнянь графічним способом; – розвивальна: формувати вміння аналізувати інформацію; розвивати увагу, логічне мислення, пам’ять; – виховна: виховувати наполегливість у досягненні мети, зацікавленість у пізнанні нового, скрупульозність; Тип уроку : засвоєння нових […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 28. Розв’язування систем двох лінійних рівнянь з двома змінними способом підстановки Графічний спосіб розв’язування систем рівнянь є досить громіздким і до того ж не завжди допомагає знайти точні розв’язки. Розглянемо інші (не графічні) способи розв’язування систем лінійних рівнянь з двома змінними, які називають аналітичними. Почнемо зі способу […]...
- Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Урок № 73 Тема. Системи двох лінійних рівнянь із двома змінними та графічний спосіб розв’язування систем Мета: засвоїти знання щодо залежності кількості розв’язків системи лінійних рівнянь від співвідношення коефіцієнтів a, b, c цих рівнянь; вироблення вмінь застосовувати названу ознаку під час графічного розв’язання систем рівнянь; подальше вдосконалювати вміння розв’язувати системи лінійних рівнянь графічним способом. Тип […]...
- Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 29. Розв’язування систем двох лінійних рівнянь з двома змінними способом додавання Тепер розглянемо ще один аналітичний спосіб розв’язування систем двох лінійних рівнянь з двома змінними – спосіб додавання. Розв’язуючи систему способом додавання, ми переходимо від даної системи до рівносильної їй системи, одне з рівнянь якої містить лише […]...
- Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними УРОК № 30 Тема. Системи рівнянь з двома змінними. Графічний спосіб розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про зміст означень: графік рівняння з двома змінними, система рівнянь з двома змінними, розв’язок системи рівнянь з двома змінними, а також алгоритмів побудови графіка рівняння з двома змінними та графічного способу розв’язування системи […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Урок № 75 Тема. Розв’язування систем лінійних рівнянь із двома змінними способом підстановки Мета: закріпити знання алгоритму розв’язування систем лінійних, рівнянь із двома змінними способом підстановки; вдосконалити вміння і навички, необхідні для застосування названого алгоритму; повторити матеріал попередньої теми щодо кількості розв’язків системи лінійних рівнянь залежно від співвідношення відповідних коефіцієнтів рівнянь. Тип уроку: засвоєння вмінь […]...
- Система двох лінійних рівнянь із двома невідомими – РІВНЯННЯ Формули й таблиці МАТЕМАТИКА РІВНЯННЯ Система двох лінійних рівнянь із двома невідомими – сталі. Правило Крамера: Квадратний тричлен – тричлен виду у = ах2 + bх + с, де х – змінна, а, b, с – константи і а ≠ 0. Одночлен ах2 називають старшим членом квадратного тричлена, а коефіцієнт а – старшим коефіцієнтом. Квадратний […]...
- Розв’язування систем лінійних рівнянь із двома змінними способом додавання Урок № 76 Тема. Розв’язування систем лінійних рівнянь із двома змінним способом додавання Мета: сформувати в учнів усвідомлення необхідності знання алгоритму розв’язування лінійних рівнянь способом додавання та розуміння кожного кроку в цьому алгоритмі; виробити вміння використовувати названий алгоритм під час розв’язування систем лінійних рівнянь. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент […]...
- Рівняння з двома змінними – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Рівняння з двома змінними Лінійним рівнянням з двома невідомими Називається рівняння виду , де x і y – невідомі, a, b, і с – числа (Коефіцієнти рівняння). Розв’язком рівняння з двома невідомими називається пара значень невідомих, при яких рівняння перетворюється у правильну числову рівність. Наприклад: ; – розв’язок рівняння, […]...
- Системи лінійних рівнянь з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Системи лінійних рівнянь з двома невідомими Якщо треба знайти спільні розв’язки кількох рівнянь, то кажуть, що ці рівняння утворюють Систему рівнянь. Розв’язок системи рівнянь з двома невідомими – пара значень невідомих, яка є розв’язком кожного з рівнянь системи. Розв’язати систему рівнянь означає знайти всі її розв’язки або довести, що […]...
- Рівняння з двома змінними 909. Рівняннями з двома змінними є рівняння; 1), 3), 5), 6), 8), 9). 910. 1) 4x + 3y = 1; 4 • (-2) + 3 • 3 = 1 – правильна рівність, тому (-2; 3) – розв’язок даного рівняння. 2) x2 + 5 = у2; (-2)2 + 5 = 32 – правильна рівність, тому (-2; […]...
- Розв’язування систем лінійних рівнянь з двома змінними способом додавання Урок № 77 Тема. Розв’язування систем лінійних рівнянь з двома змінними способом додавання Мета: закріпити знання алгоритму розв’язання систем лінійних рівнянь із двома змінними способом додавання; відпрацювати вміння і навички, використання яких передбачено алгоритмом; ознайомити учнів із нестандартними задачами на застосування систем. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент 1. Перевірка […]...
- Системи рівнянь з двома змінними УРОК 64 Тема. Системи рівнянь з двома змінними Тестові завдання 1. Яка з пар чисел є розв’язком рівняння 3х2 – 2ху +1 = 0 ? А) (1; 2); б) (2; 2); в) (0; 3); г) (0;0)? 2. Яка з пар чисел є розв’язком системи А) (3; 0); б) (2; 1); в) (1; 2); г) (0; […]...
- АНАЛІТИЧНІ СПОСОБИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &24. АНАЛІТИЧНІ СПОСОБИ РОЗВ’ЯЗУВАННЯ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ ІЗ ДВОМА ЗМІННИМИ Ви вже знаєте, що систему лінійних рівнянь із двома змінними можна розв’язати графічно. Проте існують інші, більш точні способи розв’язування таких систем – аналітичні способи. У цьому параграфі ви дізнаєтесь про два з них. До аналітичних способів розв’язування […]...
- Системи лінійних рівнянь із двома змінними Урок № 82 Тема. Системи лінійних рівнянь із двома змінними Мета: перевірити рівень опанування учнями навчального матеріалу та вироблених умінь і навичок з теми, передбачених програмою з математики. Тип уроку: контроль засвоєння знань, умінь, навичок. Хід уроку І. Організаційний момент 1. Перевірка готовності до уроку. 2. Зібрати зошити з домашньою контрольною роботою. II. Умова тематичної […]...
- Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...
- Графік лінійного рівняння з двома змінними Розв’яжіть задачі. 1078. мал. 74. Графіком лінійного рівняння з двома змінними є пряма. 1079. 1) с = 0; 2) а = 0; 3) b = 0; 4) а = 0; с = 0; 5) b = 0; с = 0. 1080. 1) -6 – 2 • 2,5 + 1 ≠ 0; -5 – 5 ≠ […]...
- Аналітичні способи розв’язування систем лінійних рівнянь із двома змінними Розв’яжіть задачі 1121. 1) х = 2y + 3; 2); х = -3у – 9; 3) х = 2у – 2,5; 4) х = 2y – 3. 1122. 1) у = 15 – 5х; 2) у = 4х + 6; 3) у = 6 – 2х; 4) у = 2 + 1,5х. 1123. 1) 2y […]...
- Лінійне рівняння з двома змінними та його графік Урок № 70 Тема. Лінійне рівняння з двома змінними та його графік Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння […]...
- Графік лінійного рівняння з двома невідомими – Системи лінійних рівнянь Математика – Алгебра Системи лінійних рівнянь Графік лінійного рівняння з двома невідомими Графіком рівняння з двома невідомими називається множина всіх точок координатної площини, координати котрих є розв’язками цього рівняння. Графіком рівняння , у якому хоча б один із коефіцієнтів (a або b) відмінний від нуля, є пряма. Для побудови будь-якої прямої досить знати координати двох […]...
- Графік рівняння з двома змінними УРОК № 28 Тема. Графік рівняння з двома змінними Мета уроку: домогтися засвоєння учнями змісту: означення графіка рівняння з двома змінними; схеми дій для побудови графіка рівняння з двома змінними. Виробити вміння: відтворювати зміст вивченого означення та алгоритму; застосовувати їх для розв’язування вправ на побудову графіків рівнянь з двома змінними. Тип уроку: узагальнення та систематизація […]...
- Розв’язування систем рівнянь з двома змінними УРОК № 33 Тема. Розв’язування систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про різні способи розв’язування систем рівнянь з двома змінними та випадки їх застосування. Закріпити вміння: за видом системи визначати оптимальний спосіб її розв’язування, описувати дії відповідно до обраного способу розв’язування системи рівнянь з двома змінними, а також виконувати дії відповідно […]...
- Лінійне рівняння з двома змінними і його графік Урок № 71 Тема. Лінійне рівняння з двома змінними і його графік Мета: вдосконалювати уміння перетворювати лінійні рівняння з двома змінними та знаходити їх розв’язки, а також будувати графіки лінійних рівнянь із двома змінними (залежно від значень а, b, с), працювати з графіками; здійснити діагностику засвоєння основних понять і вмінь, передбачених програмою за темою “Рівняння […]...
- Рівняння із двома змінними та його розв’язок Урок № 69 Тема. Рівняння із двома змінними та його розв’язок Мета: сформувати уявлення про рівняння із двома змінними та його розв’язки; усвідомити зміст поняття “графік рівняння із двома змінними”; виробити вміння: відбирати перевіркою розв’язки рівняння із двома змінними; працювати з готовим графіком рівняння із двома змінними; перетворювати рівняння виду у = f(x) та обчислювати […]...
- ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &22. ГРАФІК ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що кожній упорядкованій парі чисел відповідає певна точка на координатній площині. Оскільки кожний розв’язок рівняння з двома змінними х і у – це упорядкована пара чисел, то всі його розв’язки можна зобразити точками па координатній площині. У цих точок […]...
- Графік лінійного рівняння із двома змінними 894. (0; 1); (-1; 0); (2; 3). 895. 2х – у = 1. А) A(1; 1) – належить графіку даного рівняння, бо 2 • 1 – 1 = 1 – правильна рівність; Б) В(2; 1) – не належить графіку даного рівняння, бо 2 • 2 – 1 = 1 – неправильна рівність; В) С(0; 1) […]...
- Підсумковий урок з теми “Системи рівнянь з двома змінними” УРОК № 37 Тема. Підсумковий урок з теми “Системи рівнянь з двома змінними” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Системи рівнянь з двома змінними вищих степенів” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. Провести корекційну роботу з метою усунення причин найтиповіших […]...
- Розв’язування рівнянь графічним способом Математика – Алгебра Функції Розв’язування рівнянь графічним способом За допомогою графіків функцій можна розв’язувати рівняння графічним способом. Для цього треба побудувати в одній системі координат графіки обох частин рівняння й знайти абсциси точок їх перетину. Приклад. Розв’яжіть рівняння . Побудуємо графіки функції і в одній координатної системі (див. рисунок) і знайдемо абсиси точок їх перетину. […]...
- Розв’язання систем лінійних рівнянь способом додавання Рівень А Відповідь: (4; 3). Відповідь: (-2; -3). Відповідь: (0,5; 1). Відповідь: (-1;2). Відповідь: (-2; 4). Відповідь: (5; 1). Відповідь: (3; -1). Відповідь: (0; -2). Відповідь: (-1; 3). Відповідь: (-1; -1). Відповідь: (2; -2). Відповідь: (4; -3). Відповідь: (-0,5; 0,5). Відповідь: (1; -1). Відповідь: (1; -2). Відповідь: (1; -2). Відповідь: (5; 6). Відповідь: (5; 0,5). […]...
- Розв’язування текстових задач складанням систем рівнянь з двома змінними УРОК № 36 Тема. Розв’язування текстових задач складанням систем рівнянь з двома змінними Мета уроку: закріпити знання учнів про загальну схему розв’язування текстових задач складанням систем рівнянь з двома змінними; доповнити ці знання уявленням про спосіб міркувань при розв’язуванні задач на відсотковий склад речовин. Працювати над виробленням навичок розв’язувати за загальною схемою текстові задачі різного […]...
- ЛІНІЙНЕ РІВНЯННЯ З ДВОМА ЗМІННИМИ РОЗДІЛ 5 ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ &21. ЛІНІЙНЕ РІВНЯННЯ З ДВОМА ЗМІННИМИ Ви знаєте, що рівняння можуть бути як з однією змінною, так і з двома змінними. Наприклад, 5(2х + у) = 15 – це рівняння з двома змінними х і у. На відміну від рівняння з однією змінною, рівняння з двома змінними може […]...
- Розв’язування задач за допомогою систем лінійних рівнянь Розділ 3. ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ & 30. Розв’язування задач за допомогою систем Лінійних рівнянь Ми вже розглядали задачі, які можна розв’язати за допомогою рівнянь. Математичною моделлю задачі може бути не тільки рівняння, а й система рівнянь. Зазвичай це має відношення до тих задач, де невідомими є значення двох або більшої кількості величин. Приклад […]...
- Розв’язування систем рівнянь Математика – Алгебра Розв’язування систем рівнянь Розглянемо системи рівнянь, в яких одне або обидва рівняння другого степеня. 1. Щоб розв’язати систему рівнянь графічним способом, треба побудувати в одній системі координат графіки обох рівнянь системи й знайти координати точок перетину графіків. Ці точки і будуть розв’язками системи рівнянь. Наприклад: Графіком першого рівняння є коло з центром […]...
- РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ДОПОМОГОЮ СИСТЕМ ЛІНІЙНИХ РІВНЯНЬ Цілі: – навчальна: сформувати вміння складати системи рівнянь за умовою задачі; домогтися засвоєння схеми розв’язання задачі за допомогою системи лінійних рівнянь з двома змінними; – розвивальна: сприяти розвитку логічного мислення, уваги учнів; формувати вміння грамотно формулювати власні думки; – виховна: виховувати позитивне ставлення до навчання, старанність, спостережливість; Тип уроку : засвоєння нових знань, умінь, навичок. […]...
- Розв’язування систем лінійних рівнянь методом додавання 1047. Відповідь: (7; -1). Відповідь: (3; 5). Відповідь: (4; -1/3). Відповідь: (-1; 10). Відповідь: (-1; 16). Відповідь: (2; -3). 1048. Відповідь: (4; -4). Відповідь: (2; 2). Відповідь: (1; 1). Відповідь: (2; -1). 1049. Відповідь: (8; 1). Відповідь: (1,2; 0). Відповідь: (-1; -2). Відповідь: (7; -1). Відповідь: (4; -1). Відповідь: (6; -2). Відповідь: u = 2, […]...
ГЛІКОГЕН »