Тестові завдання
ДОДАТКИ
Тестові завдання
Тестове завдання 1
Варіант 1
1. У трикутнику ABC АВ = ВС,  ABC = 36°. Знайдіть зовнішній кут трикутника при вершині С.
ABC = 36°. Знайдіть зовнішній кут трикутника при вершині С.
А | Б | В | Г |
144° | 120° | 110° | 108° |
2. Кути трикутника відносяться як 1:2:6. Чому дорівнює сума найбільшого й найменшого кутів трикутника?
А | Б | В | Г |
90° | 100° | 120° | 140° |
3.
А | Б | В | Г |
90° | 180° | 270° | Залежить від величини кутів? і? |
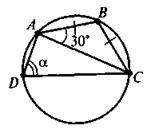
4. На рисунку зображено рівнобедрений трикутник ABC (АВ = ВС), вписаний у коло. Чому дорівнює кут??
А | Б | В | Г |
150° | 120° | 90° | 60° |
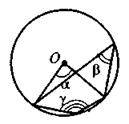
5. На рисунку
А | Б | В | Г |
? = ? | ? = ? | ? = | ? = |
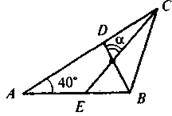
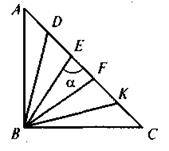
6. У трикутнику ABC, зображеному на рисунку, АВ = ВС,  A = 40°, відрізки СЕ і BD – бісектриси. Чому дорівнює величина кута??
A = 40°, відрізки СЕ і BD – бісектриси. Чому дорівнює величина кута??
А | Б | В | Г |
50° | 60° | 70° | 90° |
Варіант 2
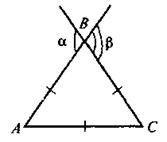
1. На рисунку зображено рівносторонній трикутник ABC. Чому дорівнює сума кутів? і??
А | Б | В | Г |
60° | 120° | 240° | 180° |
2. Знайдіть найбільший кут трикутника, якщо його кути відносяться як 2:3:5.
А | Б | В | Г |
18° | 36° | 54° | 90° |
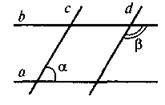
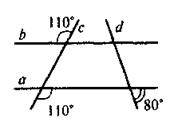
3. Які із зображених на рисунку прямих паралельні?
А | Б | В | Г |
А || b | C || d | A || d | На рисунку немає паралельних прямих |
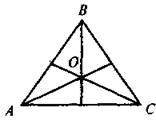
4. На рисунку зображено рівносторонній трикутник ABC, О – точка перетину його бісектрис. Чому дорівнює кут ВОС?
А | Б | В | Г |
150° | 135° | 90° | 120° |
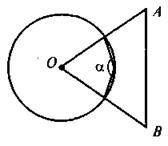
5. На рисунку зображено коло з центром О і правильний трикутник ОАВ. Чому дорівнює кут а?
А | Б | В | Г |
150° | 135° | 120° | 90° |
6. Трикутник ABC, зображений на рисунку, прямокутник рівнобедрений. Відрізки BD, BE, BF і ВК поділяють прямий кут на 5 рівних кутів. Чому дорівнює кута?
А | Б | В | Г |
54° | 60° | 63° | 81° |
Тестове завдання 2
Варіант 1
1. З точки кола проведені дві хорди. Одна з них стягує дугу 100°, а друга – 80°. Обчисліть кут між цими хордами.
А | Б | В | Г |
180° | 90° | 100° | 80° |
2. Хорда стягує дугу 60°. Обчисліть гострий кут, утворений цією хордою і дотичною до кола в кінці хорди.
А | Б | В | Г |
30° | 60° | 45° | 20° |
3. Хорда довжиною 30, перпендикулярна до діаметра і ділить його на відрізки у відношенні 1 : 9. Обчисліть радіус кола.
А | Б | В | Г |
45 | 50 | 90 | 25 |
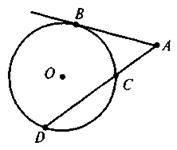
4. Пряма АВ дотикається до кола з центром О, AD – січна, AC = 4, CD = 5 (див. рис). Знайдіть АВ.
А | Б | В | Г |
13 | 6 | 36 | 20 |
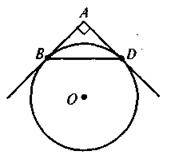
5. АВ і AD – дотичні до кола. В і D – точки дотику. АВ = 5,  BAD = 90°. Знайдіть BD (див. рис).
BAD = 90°. Знайдіть BD (див. рис).
А | Б | В | Г |
2,5 | 5 | 5 | Визначити неможливо |
6. У колі проведено дві хорди, що перетинаються. Одна з них ділиться точкою перетину на відрізки 2 і 6, а довжина другої – 7. Знайдіть відрізки другої хорди.
А | Б | В | Г |
6 і 1 | Визначити неможливо | 2 і 5 | 3 і 4 |
Варіант 2
1. З точки кола проведені дві хорди. Одна з них стягує дугу 80°. Обчисліть дугу, яку стягує друга хорда, якщо кут між хордами дорівнює 90°.
А | Б | В | Г |
180° | 90° | 100° | 80° |
2. Кут між радіусами, проведеними до кінців хорди, дорівнює 40°. Обчисліть кут між цією хордою і дотичною до кола в кінці хорди.
А | Б | В | Г |
70° | 20° | 90° | 40° |
3. Хорда довжиною 30, перпендикулярна до діаметра і ділить його на відрізки, різниця між якими дорівнює 40. Обчисліть радіус кола.
А | Б | В | Г |
50 | 45 | 25 | 90 |
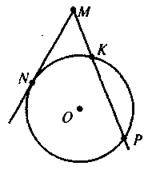
4. Пряма MN дотикається до кола з центром О, N – точка дотику, MP – січна. MN = 12, KP = 7 (див. рис). Знайдіть MP.
А | Б | В | Г |
8 | 16 | 9 | 25 |
5. AB і AD – дотичні до кола. В і D – точки дотику. Знайдіть BD, якщо  ABD = 60°, АВ = 6 (див. рис).
ABD = 60°, АВ = 6 (див. рис).
А | Б | В | Г |
3 | 6 | 12 | Визначити неможливо |
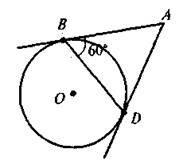
6. У колі проведено дві хорди, що перетинаються. Одна з них ділиться точкою перетину на відрізки 3 і 12, а друга – навпіл. Знайдіть довжину другої хорди.
А | Б | В | Г |
Визначити неможливо | 6 | 12 | 15 |
Тестове завдання 3
Варіант 1
1. Знайдіть гіпотенузу прямокутного трикутника з катетами 2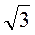 См і 2 см.
См і 2 см.
А | Б | В | Г |
4 | 4 см | 8 | 16 см |
2. У трикутнику ABC  A = 90°,
A = 90°,  B = 30°, АВ = 6 см. Знайдіть інші сторони трикутника.
B = 30°, АВ = 6 см. Знайдіть інші сторони трикутника.
А | Б | В | Г |
4 | 12 см, 6 | 12 | 3 см, 3 |
3. У трикутнику ABC  C = 90°, АС = 3 см, ВС = 18см. Знайдіть tg
C = 90°, АС = 3 см, ВС = 18см. Знайдіть tg А.
А.
A | Б | В | Г |
| 6 | 9 |
|
4. На рисунку зображено прямокутний трикутник ABC із гіпотенузою АВ, відрізок CD – висота даного трикутника.  B = 30°, AD = 2 см. Яка довжина відрізка АС?
B = 30°, AD = 2 см. Яка довжина відрізка АС?
А | Б | В | Г |
2 | 6 см | 3 | 4 см |
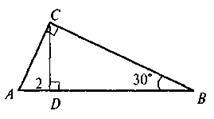
5. З вершини В прямого кута трикутника ABC на гіпотенузу опущено перпендикуляр BD, що ділить її на відрізки AD = 2 см, DC = 18 см. Знайдіть BD.
А | Б | В | Г |
6 см | 36 см | 12 см | 720 см |
6. Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює 5 см, а відстань від основи медіани до одного з катетів – 3 см. Знайдіть периметр трикутника.
А | Б | В | Г |
12 см | 10 см | 24 см | 14 см |
Варіант 2
1. Знайдіть гіпотенузу прямокутного трикутника з катетами 4 см і 2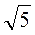 См.
См.
А | Б | В | Г |
6 см | 6 | 9 см | 3 |
2. У прямокутному трикутнику ABC  C =90°, АС = 12 см, tg
C =90°, АС = 12 см, tg A =
A = 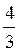 . Знайдіть катет ВС.
. Знайдіть катет ВС.
А | Б | В | Г |
16 см | 9 см | 12 см | 18 см |
3. У трикутнику ABC  C = 90°, АВ = 26 см, ВС = 24 см. Знайдіть sin
C = 90°, АВ = 26 см, ВС = 24 см. Знайдіть sin В.
В.
А | Б | В | Г |
|
|
|
|
4. На рисунку зображено прямокутний трикутник ABC з гіпотенузою АВ, відрізок CD – висота даного трикутника,  ACD = 30°, AC = 3 см. Яка довжина відрізка АВ?
ACD = 30°, AC = 3 см. Яка довжина відрізка АВ?
А | Б | В | Г |
3 | 4 | 6 см | 12 см |
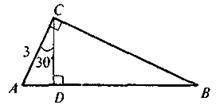
5. З вершини С прямого кута трикутника ABC на гіпотенузу опущено перпендикуляр CD, що ділить її на відрізки AD і BD. Знайдіть АВ, якщо АС = 15 см і AD = 3см.
А | Б | В | Г |
75 см | 72 см | 18 см | 5 см |
6. Один з катетів прямокутного трикутника дорівнює 6 дм, а медіана, проведена до нього, – 5 дм. Знайдіть гіпотенузу трикутника.
А | Б | В | Г |
10 дм |
| 2 | 2 |
Тестове завдання 4
Варіант 1
1. Чому дорівнює більший з кутів паралелограма, якою різниця двох із них дорівнює 24°?
А | Б | В | Г |
104° | 102° | 110° | 96° |
2. Діагональ квадрата дорівнює 5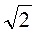 см. Знайдіть периметр квадрата.
см. Знайдіть периметр квадрата.
А | Б | В | Г |
25 см | 20 | 20 см | 10 см |
3. Точка перетину діагоналей прямокутника віддалена від його сторін на 2 см і 3 см. Знайдіть периметр прямокутника.
А | Б | В | Г |
10 см | 20 см | 10 | 12 см |
4. Периметр ромба дорівнює 80 см, а один із його кутів – 60°. Знайдіть довжину меншої діагоналі.
А | Б | В | Г |
10 см | 20 | 30 см | 20 см |
5. Гострий кут прямокутної трапеції у 4 рази менший від її тупого кута Знайдіть ці кути.
А | Б | В | Г |
40°, 160° | 60°, 120° | 45°, 135° | 36°, 144° |
6. Одна з основ трапеції на 8 см більша за іншу, а середня лінія трапеції дорівнює 10 см. Знайдіть меншу основу трапеції.
А | Б | В | Г |
6 см | 8 см | 2 см | 4 см |
Варіант 2
1. Сторони паралелограма пропорційні числам 3 і 7. Знайдіть ці сторони, якщо периметр паралелограма дорівнює 40 см.
А | Б | В | Г |
6 см, 14 см | 12 см, 28 см | 3 см, 7 см | 9 см,21 см |
2. Периметр квадрата дорівнює 20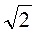 см. Знайдіть його діагональ.
см. Знайдіть його діагональ.
А | Б | В | Г |
5 см | 10 см | 5 | 10 |
3. Відстань від точки перетину прямокутника до сторони, дорівнює 5 см. Довжина цієї сторони дорівнює 2 см. Знайдіть периметр прямокутника.
А | Б | В | Г |
7 см | 9 см | 18 см | 14 см |
4. Один із кутів ромба дорівнює 60°, а довжина меншої діагоналі – 10 см. Знайдіть периметр ромба.
А | Б | В | Г |
40 | 80 см | 40 см | 60 см |
5. Чому дорівнює менший із кутів рівнобічної трапеції, якщо один із них у 5 разів більший за інший?
А | Б | В | Г |
20° | 15° | 30° | 60° |
6. Одна з основ трапеції на 6 см менша за іншу, а середня лінія трапеції дорівнює 8 см. Знайдіть більшу основу трапеції.
А | Б | В | Г |
5 см | 11 см | 9 см | 12 см |
Тестове завдання 5
Варіант 1
1°. Периметр паралелограма 18 см. Чому дорівнюють сторони паралелограма, якщо одна з них удвічі більша за іншу?
A. 6 см і 12 см.
Б. 4 см і 8 см.
B. 3 см і 6 см.
Г. 4 см і 5 см.
2°. У ромба ABCD величина кута D – 140°. Визначте кути трикутника AOD (О – точка перетину діагоналей ромба).
A. 70°, 70°, 40°.
Б. 20°, 70°, 90°.
B. 20°, 20°, 140°.
Г. Інша відповідь.
3°. ABCD – прямокутник, АС = 18 см, CD = 7 см. Чому дорівнює периметр трикутника COD?
A. 43 см.
Б. 21,5 см.
B. 25 см.
Г. 12,5 см.
4. Сторони паралелограма дорівнюють 3 см і 5 см. Чи може діагональ цього паралелограма дорівнювати:
A. 10 см.
Б. 8 см.
B. 8,5 см.
Г. 4 см?
5. Периметр прямокутника 12 дм. Чому дорівнює сума відстаней довільної внутрішньої точки цього прямокутника до його сторін?
А. 12 дм.
Б. 6 дм.
В. 3 дм.
Г. Не можна визначити.
6. Як перевірити, чи є вирізаний з картону чотирикутник ромбом?
A. Виміряти довжини всіх його сторін і порівняти їх між собою.
Б. Провести діагоналі й виміряти кут між ними.
B. Виміряти та порівняти величини протилежних кутів.
Г. Інший спосіб.
7*. Довжини діагоналей даного чотирикутника т і п. Знайдіть периметр чотирикутника, вершини якого лежать на серединах сторін даного трикутника.
A. 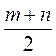 .
.
Б. m + n.
B. 2(m + n).
Г. 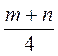 .
.
8*. Чи можна побудувати чотирикутник, що не є прямокутником, діагоналі якого рівні між собою? Проілюструйте свою відповідь.
9**. Бісектриса кута В прямокутника ABCD поділяє сторону AD на відрізки завдовжки 3 см і 7 см. Чому дорівнює периметр прямокутника?
A. 34 см.
Б. 26 см.
B. 29 см.
Г. Інша відповідь.
10**. Дано паралелограм ABCD. На його сторонах ВС і AD взято, відповідно, точки Е і F так, що BE = DF, О – точка перетину BD та EF. Укажіть, які з тверджень правильні.
A. BEFA – паралелограм.
Б. BO > OD.
B. Пряма АС проходить через точку О.
Г. BE + AF < AD.
11**. Дано квадрат ABCD, АЕ = BE = CK = DL. Доведіть, що EFKL – квадрат.
12**. Даний відрізок поділіть на два відрізки так, щоб їх довжини були пропорційні числам 1 і 2.
Варіант 2
1°. Одна зі сторін паралелограма в 4 рази менша за другу, а його периметр 30 см. Чому дорівнюють сторони паралелограма?
A. 6 см і 24 см.
Б. 3 см і 12 см.
B. 12 см і 18 см.
Г. 5 см і 20 см.
2°. У ромба MNKL величина кута N – 100°. Визначте кути трикутника MON (О – точка перетину діагоналей ромба).
A. 40°, 40°, 100°.
Б. 50°, 50°, 80°.
B. 40°, 50°, 90°.
Г. Інша відповідь.
3°. MNPQ – прямокутник, NP = 5 см, МР = 12 см. Чому дорівнює периметр трикутника NOP?
A. 16 см.
Б. 17 см.
B. 29 см.
Г. 22 см.
4. Сторони паралелограма 2 дм і 7 дм. Чи може діагональ цього паралелограма дорівнювати:
A. 8 см.
Б. 9 см.
B. 9,5 см.
Г. 10 см?
5. Периметр прямокутника 36 м. Чому дорівнює сума відстаней довільної внутрішньої точки цього прямокутника до його сторін?
A. 9 м.
Б. 18 м.
B. 36 м.
Г. Не можна визначити.
6. Кравець викроїв з тканини чотирикутник, який має бути ромбом. Як перевірити правильність виготовлення викрійки, не користуючись інструментами?
A. Перегнути викрійку по діагоналі.
Б. Перегнути викрійку по лінії, що проходить через середини протилежних сторін.
B. Послідовно перегнути викрійку по обох діагоналях.
Г. Інший спосіб.
7*. Периметр чотирикутника, вершини якого лежать на серединах сторін даного чотирикутника, дорівнює 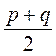 . Знайдіть довжини діагоналей даного чотирикутника.
. Знайдіть довжини діагоналей даного чотирикутника.
A. р і q.
Б. 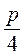 і
і 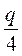 .
.
B. 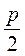 і
і 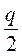 .
.
Г. 2р і 2q.
8*. Чи обов’язково чотирикутник, який має два прямі кути, є прямокутником? Проілюструйте свою відповідь.
9*. Бісектриса тупого кута В паралелограма ABCD поділяє сторону AD навпіл. Чому дорівнює периметр паралелограма, якщо його менша сторона дорівнює 8 см?
A. 24 см.
Б. 48 см.
B. 32 см.
Г. Не вистачає даних, щоб визначити.
10**. Дано паралелограм A BCD. Пряма, що проходить через точку перетину діагоналей О, перетинає сторони ВС та AD, відповідно, у точках Е та F. Які з наступних тверджень правильні? Позначте їх.
A. Периметри трикутників BFO і DFO обов’язково однакові.
Б. EO + OF може дорівнювати АВ.
B. EC може бути більше за AF.
Г. BE + AF = BC.
11**. Дано квадрат ABCD, AE = CF. Доведіть, що BEDF – ромб.
12**. Даний відрізок поділіть на два відрізки так, щоб довжини цих відрізків були пропорційні до числам 2 і 3.
Тестове завдання 6
Варіант 1
1°. Довжина середньої лінії трапеції 7 дм, а однієї з основ 5 дм. Чому дорівнює довжина другої основи?
A. 14 дм.
Б. 10 дм.
B. 9дм.
Г. 6 дм.
2°. Пряма СМ, яка паралельна бічній стороні АВ трапеції ABCD, поділяє основу AD на відрізки AM = 5 см і MD = 4 см. Чому дорівнює середня лінія трапеції?
A. 7 см.
Б. 4,5 см.
B. 2,5 см.
Г. 2 см.
3°. Даний відрізок поділіть на чотири рівні відрізки.
4. Основи трапеції мають довжини 8,2 см і 14,2 см. Якою є відстань між серединами діагоналей цієї трапеції?
A. 4,1 см.
Б. 7,1 см.
B. 3 см.
Г. 11,2 см.
5. Кінці діаметра віддалені від дотичної до кола на 2,8 мі 1,2 м. Знайдіть довжину діаметра й позначте правильну відповідь.
A. 2 м.
Б. 4 м.
B. 1,6 м.
Г. 0,8 м.
6. У рівнобічній трапеції ABCD точки К, L, М, N – середини її сторін АВ, ВС, CD і AD, відповідно. Периметр чотирикутника KLMN дорівнює 40 см. Чому дорівнюють діагоналі трапеції?
A. 20 см і 20 см.
Б. 10 см і 30 см.
B. 40 см і 40 см.
Г. Інша відповідь.
7*. Чому дорівнює довжина відрізка ВВ1?
A. 12.
Б. 21.
B. 3.
Г. 9.
8*. Доведіть, що середини сторін рівнобічної трапеції є вершинами ромба.
9*. На прямій а взято точки А1, А2, А3, А4 так, що A1A2 = 3 м, А2А3 = 2 м, А3А4 = 5 м. Через точки А1, А2, А3, А4 проведено паралельні прямі, які перетинають пряму b у точці В1, В2, В3, В4, відповідно. Чиє серед відповідей правильні? Якщо є – позначте їх.
А. 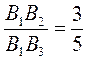 .
.
Б. В3В4 = В1В2 + В2В3.
В. В1В2 < В2В3.
Г. Якщо В3В4 = 10 м, то В2В3 = 5 м.
10**. Побудуйте трапецію ABCD за такими елементами: AD, ВС і АВ.
11**. Доведіть, що сума бічних сторін трапеції більша за різницю основ.
12**. Проекції двох сторін гострокутного трикутника ABC на пряму АС мають довжини 6 см і 4 см. Яку довжину мають проекції медіан цього трикутника на ту саму пряму?
A. 1 см, 8 см, 7 см.
Б. 2 см, 3 см, 3 см.
B. 5 см, 3 см, 2 см.
Г. Інша відповідь.
Варіант 2
1°. Більша основа трапеції дорівнює 8 см, а менша на 2 см коротша за середню лінію. Чому дорівнює середня лінія трапеції?
A. 6 см.
Б. 4 см.
В. 7 см.
Г. 12 см.
2°. Паралельно бічній стороні CD трапеції ABCD проведено пряму ВК. Основа ВС = 5 дм, середня лінія MN = 8 дм. Чому дорівнює довжина відрізка АК, який пряма ВК відтинає на основі AD?
А. 5 дм.
Б. 6 дм.
В. 11 дм.
Г. 9 дм.
3°. Поділіть даний відрізок на п’ять рівних відрізків.
4. Менша основа трапеції має довжину 6,2 см, відстань між серединами діагоналей цієї трапеції дорівнює 4 см. Якою є довжина більшої основи?
A. 3,1 см.
Б. 8 см.
B.14,2 см.
Г. 10,2 см.
5. Один кінець діаметра, що дорівнює 2,6 см, віддалений від дотичної до кола на 1,4 м. Знайдіть, на якій відстані від цієї дотичної знаходиться другий кінець діаметра. Позначте правильну відповідь.
A. 4 м.
Б. 1,2 м.
B. 3,8 м.
Г. 6,8 м.
6. Діагоналі KM і LN трапеції дорівнюють 18 см і 12 см. Чому дорівнює периметр трапеції?
A. 30 см.
Б. 15 см.
B. 54 см.
Г. Інша відповідь.
7*. Чому дорівнює довжина відрізка ОВ1?
A. 20.
Б. 9.
B. 2.
Г. 24,5.
8*. Бічні сторони прямокутної трапеції відносяться як 1 : 2. Знайдіть найбільший кут цієї трапеції.
9*. На стороні ON кута MON взято точки В1, В2, В3, В4 так, що В1В2 = В2В3 = В3В4. Через точки В1, В2, В3, В4 проведено паралельні прямі, які перетинають сторону ОМ кута MON, відповідно, в точках А1, А2, А3, А4. Укажіть правильне твердження.
A. А1А2 >2А4А3.
Б. А1А2 =2А3А4.
B. А2А4 < А1А2.
Г. Якщо А1А2 = 3 дм, то А2А4 = 6 дм.
10**. Побудуйте трапецію ABCD за такими елементами: AD, AB і АС.
11**. Доведіть, то різниця основ трапеції більша за різницю бічних сторін.
12**. Проекції медіан трикутника ABC на пряму АС мають довжини 16 см, 14 см і 2 см. Яку довжину мають проекції двох сторін цього трикутника на ту саму пряму?
A. 2 см і 18 см.
Б. 8 см і 12 см.
B.16 см і 16 см.
Г. Інша відповідь.
Тестове завдання 7
Варіант 1
1°. Якою є довжина сторони АВ трикутника ABC, якщо АЕ = 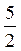 , BD =
, BD = 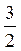 ?
?
А. 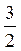 .
.
Б. 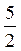 .
.
В. 3.
Г. 5.
2°. Один із кутів прямокутного трикутника дорівнює 36°, а гострі кути іншого прямокутного трикутника відносяться як 2:3. Чи подібні трикутники?
3°. Знайдіть довжину відрізка, позначеного буквою х. Укажіть правильну відповідь.
A. 21 см.
Б. 10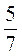 См.
См.
B. 9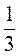 См.
См.
Г. 9 см.
4. Визначте, які з трикутників подібні, якщо сторони їх дорівнюють:
A. 4 см, 6 см, 9 см і 12 см, 18 см, 8 см;
Б. 1,5 дм, 42 см, 20 см і 21 см, 10 см, 9 см;
B. 55 см, 1,5 см, 140 см і 15 см, 14 см, 10,5 см;
Г. 14 см, 21 см, 28 см і 20 см, 15 см, 10 см.
5. Катети одного прямокутного трикутника дорівнюють 15 см і 20 см, а гіпотенуза і висота, проведена до неї, другого прямокутного трикутника відповідно дорівнюють 75 см і 26 см. Чи подібні трикутники?
6. Основи трапеції ВС = 20 см, AD = 30 см, діагоналі АС = 24 см і BD = 41 см перетинаються в точці О. Чому дорівнюють периметри трикутників ВОС і AOD?
A. 64 см і 96 см.
Б. 46 см і 69 см.
B. 52,5 см і 62,5 см.
Г. Інша відповідь.
7*. Два рівнобедрені трикутники мають рівні кути при вершинах, які протилежні основам. Основа першого трикутника дорівнює 12 см, а медіана, проведена до неї, – 8 см. Знайдіть бічну сторону другого трикутника, якщо його периметр 128 см.
A. 10 см.
Б. 40 см.
B. 32 см.
Г. 48 см.
8*. Яку висоту на плівці має зображення дерева, що знаходиться на відстані 70 м від об’єктива фотоапарата і має висоту 14 м, якщо відстань від об’єктива до зображення дорівнює 50 мм?
9*. Сторони трикутника відносяться як 7:2:6. Знайдіть сторони подібного трикутника, різниця найбільшої і найменшої сторін якого дорівнює 15 см. Укажіть правильну відповідь.
A. 147 см, 42 см, 126 см.
Б. 21см, 6 см, 18 см.
B. 63 см, 36 см, 21 см.
Г. Інша відповідь.
10**. У трикутник вписаний паралелограм, гострий кут якого співпадає з кутом трикутника. Сторони паралелограма відносяться як 3:1, а сторони трикутника, що лежать на сторонах цього кута, дорівнюють 24 см і 36 см. Визначте сторони паралелограма.
11**. На яку висоту піднявся пішохід, який пройшов 2 км прямою дорогою, що піднімається під кутом до горизонту, коли відомо, що інший пішохід, ідучи цією самою дорогою і здолавши 1,5 км, піднявся на 0,3 км?
12**. Доведіть, що в подібних трикутниках відповідні висоти пропорційні відповідним сторонам.
Варіант 2
1°. Якою є довжина сторони АВ трикутника ABC, якщо 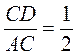 , ВС = 6?
, ВС = 6?
A. 3.
Б. 12.
B. 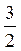 .
.
Г. 4.
2°. Один із кутів прямокутного трикутника дорівнює 54°, а різниця гострих кутів іншу прямокутного трикутника дорівнює 18°. Чи подібні трикутники?
3°. Знайдіть довжину відрізка, позначеного буквою х. Позначте правильну відповідь.
A. 8 см.
Б. 24 см.
B. 4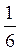 См.
См.
Г. 7,5 см.
4. Визначте, які з трикутників подібні, якщо сторони їх дорівнюють:
A. 3,5 см, 9 см, 1,1 дм і 7 см, 2,2 дм, 1,8 дм;
Б. 6 см, 4 см, 7 см і 3 см, 3,5 см, 6 см;
B. 72 см, 1,6 м, 96 см і 9 см, 12 см, 20 см;
Г. 25 см, 75 см, 60 см і 90 см, 72 см, 35 см.
5. Катет і гіпотенуза одного прямокутного трикутника відповідно дорівнюють 12 см і 15 см, а катет і висота, проведена до гіпотенузи, другого трикутника відповідно дорівнюють 45 см і 36 см. Чи подібні трикутники?
6. Основи трапеції ВС = 30 см, AD = 50 см, діагоналі АС = 40 см і BD = 48 см перетинаються в точці О. Чому дорівнюють периметри трикутників ВОС і AOD?
A. 36 см і 15 см.
Б. 63 см і 105 см.
B. 93 см і 75 см.
Г. Інша відповідь.
7*. Два рівнобедрені трикутники мають рівні кути при вершинах, які протилежні основам. Бічна сторона першого трикутника дорівнює 5 см, а основа – 6 см. Знайдіть висоту, проведену до основи другого трикутника, якщо його периметр 80 см.
A. 4 см.
Б. 25 см.
B. 20 см.
Г. 30 см.
8*. На плівці зображення дерева, що знаходиться на відстані 90 м від об’єктива фотоапарата, має висоту 10 мм. Чому дорівнює висота дерева, якщо відстань від об’єктива до зображення дорівнює 50 мм?
9*. Сторони трикутника відносяться як 5:4:2. Знайдіть сторони подібного трикутника, сума найбільшої і найменшої сторін якого дорівнює 21 см. Укажіть правильну відповідь.
A. 15 см, 12 см, 6 см.
Б. 75 см, 60 см, 30 см.
B. 35 см, 28 см. 14 см.
Г. Інша відповідь.
10**. У трикутник ABC вписаний паралелограм ADEF, гострий кут якого співпадає з кутом трикутника А. Визначте сторону АС, коли відомо, що сторони паралелограма дорівнюють 6 см і 5 см, а сторона АВ дорівнює 17 см.
11**. На ділянці дороги завдовжки 320 м підйом однаковий. Позначки про висоту над рівнем моря на кінцях ділянки 186,5 м і 194,9 м. Знайдіть позначку на відстані 120 м від початку ділянки.
12**. Доведіть, що в подібних трикутниках бісектриси відповідних кутів пропорційні відповідним сторонам.
Тестове завдання 8
Варіант 1
1°. Які з ламаних, що мають наведені довжини ланок, можуть бути замкненими?
A. 1 дм, 2 дм, 3 дм, 7 дм.
Б. 3 см, 4 см, 5 см, 7 см, 19 см.
B. 8 м, 9 м, 10 м, 24 м.
Г. 15 мм, 18 мм, 20 мм, 25 мм, 80 мм.
2°. Скільки сторін має многокутник, у якого число діагоналей, проведених з однієї вершини, дорівнює 7?
A. 9.
Б. 10.
B. 8.
Г. 7.
3°. Чому дорівнює сума внутрішніх кутів опуклого восьмикутника?
A. 1440°.
Б. 1080°.
B. 900°.
Г. 1260°.
4. Радіус кола, описаного навколо прямокутника, дорівнює 20 мм. Чому дорівнює відстань між серединами двох суміжних сторін прямокутника?
A. 10 мм.
Б. 20 мм.
B. 40 мм.
Г. 5 мм.
5. Сторони паралелограма дорівнюють 4,2 см і 5,6 см. Висота, проведена до більшої зі сторін, дорівнює 3,3 см. Чому дорівнює друга висота цього паралелограма?
A. 18,48 см.
Б. 13,86 см.
B. 7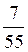 см.
см.
Г. 4,4 см.
6. Яку фігуру утворюють вершини рівновеликих трикутників, що мають спільну основу АВ?
A. Коло, діаметр якого дорівнює основі АВ;
Б. Дві прямі, паралельні основі АВ;
B. Два промені, паралельні основі АВ;
Г. Два відрізки, паралельні основі АВ.
7*. Якою є площа гострокутного трикутника, якщо його висота, проведена до основи, дорівнює 6 см, а проекції бічних сторін на цю основу дорівнюють 12 см і 4 см?
A. 48 см2.
Б. 36 см2.
B. 12см2.
Г. 144 см2.
8*. У квадрат, площа якого дорівнює 64 см2, вписано коло. Яким є радіус цього кола?
A. 32 см.
Б. 16 см.
B. 8 см.
Г. 4 см.
9**. Обчисліть площу зображеної фігури й позначте правильну відповідь.
A. 120 см2.
Б. 960 см2.
B. 100 см2.
Г. Інша відповідь.
10**. Три кути опуклого многокутника дорівнюють по 80°, усі інші – по 150°. Скільки вершин має цей многокутник?
A. 5.
Б. 6.
B. 7.
Г. 8.
11**. Який з усіх паралелограмів з діагоналями, що дорівнюють 4см і 8 см, має найбільшу площу?
A. Прямокутник.
Б. Квадрат.
B. Ромб.
Г. Паралелограм.
12**. Периметр описаної навколо кола трапеції дорівнює 30 см. Яка довжина середньої лінії цієї трапеції?
A. 15 см.
Б. 10 см.
B. 7,5 см.
Г. Не можна визначити.
Варіант 2
1°. Які з ламаних, що мають наведені довжини ланок, не можуть бути замкненими?
A. 2 м, 3 м, 5 м, 9 м.
Б. 7 см, 9 см, 10 см, 15 см, 35 см.
B. 11 дм, 14 дм, 17 дм, 42 дм.
Г. 20 мм, 60 мм, 70 мм, 85 мм, 25 мм.
2°. Скільки діагоналей, проведених з однієї вершини, має дев’ятикутник?
А. 9.
Б. 8.
В. 7.
Г. 6.
3°. Чому дорівнює сума внутрішніх кутів опуклого десятикутника?
А. 1800°.
Б. 1440°.
В. 1260°.
Г. 1620°.
4. Відстань між серединами двох суміжних сторін прямокутника дорівнює 12 см. Чому дорівнює радіус кола, описаного навколо цього прямокутника?
А. 6 см.
Б. 12 см.
В. 24 см.
Г. 48 см.
5. Сторони паралелограма дорівнюють 0,8 дм і 1 дм. Висота, проведена до меншої із сторін, дорівнює 0,6 дм. Чому дорівнює друга висота цього паралелограма?
А. 0,48 дм.
Б. 0,975 дм.
В. 1,3(3) дм.
Г. 0,048 дм.
6. Яку фігуру утворюють вершини паралелограмів, які рівновеликі даному паралелограму ABCD і мають спільну основу AD?
A. Коло, діаметр якого дорівнює AD.
Б. Дві прямі, паралельні основі AD.
B. Два промені, паралельні основі AD.
Г. Два відрізки, паралельні основі AD.
7*. Проекції бічних сторін на основу гострокутного трикутника дорівнюють 14 см і 6 см, а площа цього трикутника – 77 см2. Яку довжину має висота цього трикутника?
А. 3,85 см.
Б. 7 см.
В. 11см.
Г. 25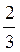 см.
см.
8*. Квадрат описаний навколо кола радіусом 6 см. Чому дорівнює площа цього квадрата?
А. 36 см2.
Б. 144 см2.
В. 9 см2.
Г. 24 см2.
9*. Обчисліть площу зображеної фігури й позначте правильну відповідь.
A. 2 м2.
Б. 6 м2.
B. 8 м2.
Г. Інша відповідь.
10**. Три кути опуклого многокутника прямі, інші – по 150°. Скільки вершин мас цей многокутник?
А. 5.
Б. 5.
В. 7.
Г. 8.
11**. Який з усіх паралелограмів зі сторонами, що дорівнюють 4 см і 8 см, має найбільшу площу?
A. Прямокутник.
Б. Квадрат.
B. Ромб.
Г. Паралелограм.
12**. Середня лінія описаної навколо кола трапеції дорівнює 14 см. Чому дорівнює периметр цієї трапеції?
A. 28 см.
Б. 42 см.
B. 56 см.
Г. Не можна визначити.
Тестове завдання 9
Варіант І
1°. Сторона прямокутника 8 см і 15 см. Чому дорівнює його діагональ?
А. 23 см.
Б. 17 см.
В. 289 см.
Г. 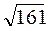 см.
см.
2°. У прямокутному трикутнику ABC ( C = 90°) АВ = 1 см,
C = 90°) АВ = 1 см,  A = 30°. Яку довжину має катет АС?
A = 30°. Яку довжину має катет АС?
A. 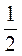 см.
см.
Б. 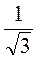 см.
см.
B. 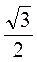 см.
см.
Г. 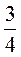 См.
См.
3°. З точки А проведено до прямої а дві похилі: АВ = 10 см і AD = 15 см. Яке з наступних тверджень є правильним?
A. Пряма АВ утворює з прямою а більший кут, ніж пряма AD.
Б. Пряма AD утворює з прямою а більший кут, ніж пряма АВ.
B. Прямі АВ і AD утворюють з прямою а однакові кути.
Г. Не можна визначити, яка з прямих. АВ чи AD, утворює з прямою а більший кут.
4. У колі проведено хорду, перпендикулярну радіусу й таку, що проходить через його середину. Чому дорівнює довжина цієї хорди, якщо діаметр кола дорівнює 8 см?
A. 2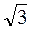 см.
см.
Б. 4 см.
B. 2 см.
Г. Інша відповідь.
5. Якою є градусна міра кута?, якщо sin? = 0,5035?
A. 30°5′.
Б. 30° 15′.
B. 59° 15′.
Г. 59°45′.
6. Кут при основі рівнобічної трапеції дорівнює 60°, а бічна сторона дорівнює меншій основі й становить 10 см. Чому дорівнює середня лінія трапеції?
A. 5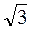 см.
см.
Б. 10 см.
B. 5 см.
Г. 15 см.
7*. Залізнична колія підіймається в горах на 0,5 м на кожні 30 м шляху. Чому приблизно дорівнює кут підйому?
A. 9°37′.
Б. 80°23′.
B. 57°.
Г. 63°.
8*. У прямокутному трикутнику ABC кут С – прямий, CD – висота, 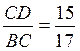 . Визначте
. Визначте 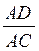 .
.
A. 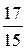 .
.
Б. 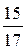 .
.
B. 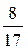 .
.
Г. Інша відповідь.
9*. Два кола, радіуси яких R і r, дотикаються зовні. Відстань між центрами кіл дорівнює d, довжина спільної дотичної, яка не проходить через точку дотику кіл, – l. Визначте, які з наступних тверджень є правильними?
A. Якщо R? r, то d? l.
Б. Якщо R? r, то R + r = l.
B. d2 – l2 = (R – r)2.
Г. l = 2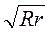 .
.
10**. Основа рівнобедреного трикутника дорівнює b. Кут при основі дорівнює?. Чому дорівнює периметр трикутника?
A. b соs?.
Б. b(cos? + 1).
B. b(2 + cos?).
Г. 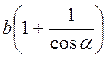 .
.
11**. На прямій MN взято точку А і з неї під гострим кутом? до прямої MN проведено відрізок АВ завдовжки а. Як змінюється величина проекції відрізка АВ на пряму MN за умови збільшення кута а від 0° до 90°?
12**. З маяка, висота якого над рівнем моря Н = 150 м, визначають відстань до пароплава, який проходить повз маяк. Кут падіння? = 9°. Чому дорівнює відстань від пароплава до маяка?
Варіант 2
1°. Ширина прямокутника 9 см, а діагональ – 15 см. Чому дорівнює довжина цього прямокутника?
А. 6 см.
Б. 144 см.
В. 12 см.
Г. 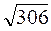 см.
см.
2°. У прямокутному трикутнику ABC ( C = 90°) АС = 3 см,
C = 90°) АС = 3 см,  A = 60°. Яку довжину має катет ВС?
A = 60°. Яку довжину має катет ВС?
А. 6 см.
Б. 1,5 см.
В. 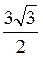 см.
см.
Г. 3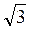 см.
см.
3°. З точки А до прямої а проведено дві похилі АВ і АС, які утворюють з нею кути 35° і 70°, відповідно. Яке з наступних тверджень є правильним?
A. Похила АВ має більшу довжину, ніж похила АС.
Б. Похила АС має більшу довжину, ніж похила АВ.
B. Похилі АВ і АС мають однакові довжини.
Г. Не можна визначити, яка з похилих – АВ чи АС, має більшу довжину.
4. У колі проведено хорду, перпендикулярну радіусу й таку, що проходить через його середину. Чому дорівнює діаметр кола, якщо довжина цієї хорди дорівнює 6 см?
A. 2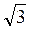 См.
См.
Б. 4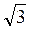 См.
См.
B. 6 см.
Г. Інша відповідь.
5. Якою є градусна міра кут?, якщо cos? = 0,8203?
А. 34°47′.
Б. 34°53′.
В. 55°13′.
Г. 55°7′.
6. У прямокутній трапеції один з кутів дорівнює 135°, середня лінія дорівнює 18 см, а основи відносяться як 1:8. Чому дорівнює менша бічна сторона трапеції?
А. 2 см.
Б. 12 см.
В. 12 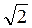 см.
см.
Г. 28 см.
7*. Кут підйому становить 36°. На скільки метрів приблизно підіймається туристична стежина на кожні 50 м шляху?
А. 83 м.
Б. 29,4 м.
В. 36, 3 м.
Г. 40,5 м.
8*. У прямокутному трикутнику ABC кут С – прямий, CD висота, 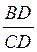 = 1,3. Визначте
= 1,3. Визначте 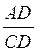 .
.
A. 1,3.
Б. 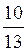 .
.
B. 0,3.
Г. Інша відповідь.
9*. Два кола, радіуси яких R і r, дотикаються зовні. Довжина спільної дотичної, яка не проходить через точку дотику кіл, дорівнює l, відстань між центрами кіл дорівнює d. Визначте, які з наступних тверджень є правильними?
A. Якщо R? r, то l > R + r.
Б. Якщо R = r, то d > l.
B. Якщо R = r, то d2 = 4R2.
Г. l2 < 4Rr.
10**. Бічна сторона рівнобедреного трикутника дорівнює а, кут при основі дорівнює а. Чому дорівнює периметр цього трикутника?
A. 2a cos?.
Б. 2a(1 + cos?).
B. a(1 + cos?).
Г. 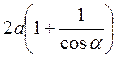 .
.
11**. На прямій KL взято точку Р і з неї під гострим кутом? до прямої KL проведено відрізок PQ завдовжки l. Як змінюється величина проекції відрізка PQ напряму KL за умови зменшення кута а від 90° до 0°?
12**. Літак посилає сигнал капітану риболовецького судна, oо він знаходиться над косяком риби на висоті H = 950 м. З судна визначають кут підйому літака? = 26°30′. Чому дорівнює відстань судна від косяку риби?
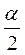
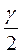
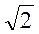
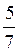
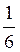
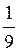
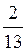
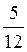
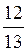
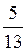
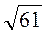 Дм
Дм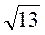 дм
дм