Тіла і поверхні обертання
905.
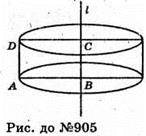
На рисунку тіло, утворене обертанням прямокутника навколо його сторони.
906.
А)
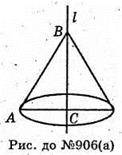
Тіло, утворене обертанням прямокутного трикутника навколо катета,
Б)
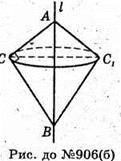
Тіло, утворене обертанням прямокутного трикутника навколо гіпотенузи.
ΔABC – прямокутний, AB – гіпотенуза.
907.
Площина симетрії тіла обертання проходить через його вісь.
908.
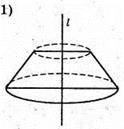
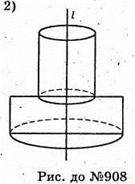
Див. рис.
909.
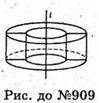
У
910.
Тіло, утворене обертанням навколо вісі опуклої плоскої фігури, опукле.
911.
Центр симетрії тіла обертання може не належати даному тілу.
912.
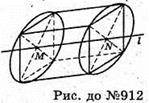
Фігура, яка утворюється при обертанні куба навколо прямої,
Що з’єднує центри протилежних граней куба.
913.
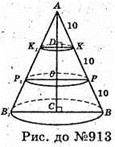
Гіпотенуза AB = 30 см,
AK = KP = PB.
ΔADK.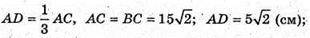 
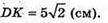
Довжина кола, яку описує точка
Де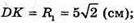 
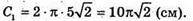
Довжина кола, яку описує точка Р: C2 = 2Πr2, де R2= OP,
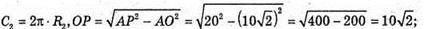
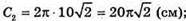
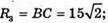
C2 = 2πR3, де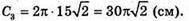 
Відповідь: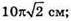 
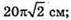
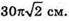
914.
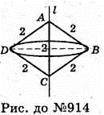
Нехай рівносторонній AABC обертається навколо його сторони
AB = BC = AC = 2 дм. Осьовий переріз – ромб ABCD.
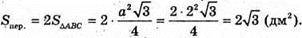
915.
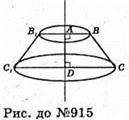
Нехай трапеція, бічна сторона якої перпендикулярна до основ, обертається навколо цієї бічної сторони. ABCD – трапеція. AD – бічна сторона. AB і DC – основи, AB + AD; DC + AD. AB = 3,5 см; DC = 5,2 см.
Основи трапеції описують круги з радіусами AB і DC.
Sкр. = π × R 2, S1 = π × AB2, S2 = π × DC2;
S1 = π × 3,52 = 12,25π (см2); S2= π × 5,22= π × 27,04π (см2).
Відповідь: 12,25π см2; 27,04π см2.
916.
Довжина газопроводу 1450 км = 1450 000 м; довжина труби 20 м.
Всього необхідно зварити 1 450 000 : 20 = 72 500 (труб).
Діаметр труби d = 1420 мм = 1,42 м.
Довжина кола перерізу труби C = π × d = 3,14 × 1,42 = 4,4588 м.
Всього електрозварювальники зварили 72 499 × 4,4588 = 323 259 м труб.
917.
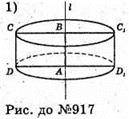
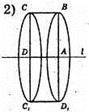
Прямокутник ABCD зі сторонами AB = 5 см і AD = 7 см
Обертається спочатку навколо сторони АВ, а потім навколо сторони AD.
S1 – площа осьового перерізу DD1C1С.
SDD1C1C = DD1 × C1 D = 14 × 5 = 70(см2);
S2- площа осьового перерізу BCC1B1.
SBCC1B1 = AD × CC1 = 10 × 7 = 70 (см2);
S1 : S2 = 70 : 70 = 1.
918.
А)
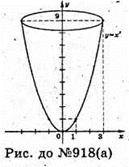
Крива задана рівнянням: у = х2, х? [0; 3].
Поверхня, яка утворюється при обертанні кривої у = x2навколо вісі Oy.
Б)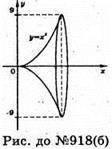 
Поверхня, яка утворюється при обертання кривої у = х2 навколо вісі Ох.
919.
А)
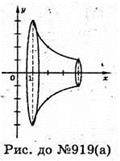
Крива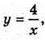 
x? [1; 4] обертається навколо осі Ох.
Фігура, утворена при обертанні кривої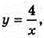 
х? [1; 4] навколо осі Ох;
Б)
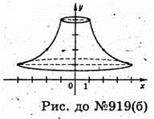
Фігура, утворена при обертанні кривої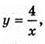 
x? [1; 4] навколо осі Oy.
В)
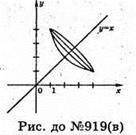
Фігура, утворена при обертанні кривої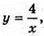 
x? [1; 4] навколо прямої у = x.
Г)
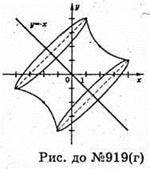
Фігура, утворена при обертанні кривої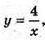 
х? [1; 4] навколо прямої у = – х.
920.
А)
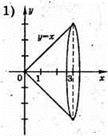
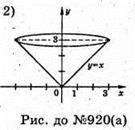
Фігура, утворена обертанням прямої у = х, x? [0; 3] навколо осі Ох.
Фігура, утворена обертанням прямої у = х, х? [0; 3] навколо осі Oy.
Б)
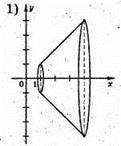
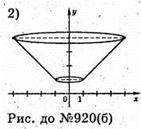
Фігура, утворена обертанням прямої у = х, х? [1; 4] навколо осі Ох.
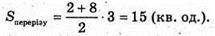
Фігура, утворена обертанням прямої у = х, х? [1; 4] навколо осі Oy.
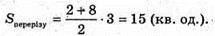
В)
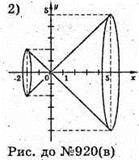
Фігура, отримана при обертанні прямої у = х навколо осі Оу, якщо x? [-2; 5].
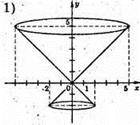
Фігура, отримана при обертанні прямої у = х навколо осі Ох, якщо x? [-2; 5].
921.
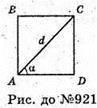
Прямокутник ABCD, AC = d, ∠CAD = α, є осьовим перерізом тіла обертання. Обертали прямокутник. AB = d × sin α; AD = d × cos а.
Розміри прямокутника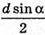 
і d cos α або d sin α і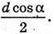 
922.
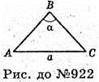
Нехай рівнобедрений ΔABC з основою а і кутом α при вершині є осьовим перерізом деякого тіла обертання.
Обертали прямокутний трикутник. Розміри фігури: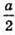 
і 
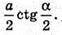
923.
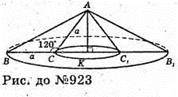
Нехай ΔАВС, у якого AC = BC = a, ∠C = 120°, обертається навколо прямої, яка містить висоту трикутника, проведену з вершини A, AK + BC.
ΔAKC – прямокутний.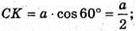 
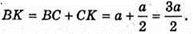
Вершина В опише коло радіусом BK, довжина кола C = 2π × R;
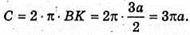
Вершина C опише коло радіусом CK, довжина кола
C = 2πR = с = 2 × π × а = 2πa.
Відповідь: 2πa; 3πa.
924.
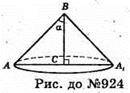
Нехай прямокутний ΔABC обертається навколо меншого катета ВС, який утворює з гіпотенузою кут α.
Нехай AC = R, тоді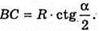 
Площа осьового перерізу:
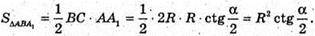
Площа круга описаного більшим катетом AC Sкр. = πR2.
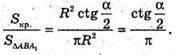
925.
Нехай квадрат ABCD обертається навколо прямої, яка проходить через точку А паралельно діагоналі BD.
А)
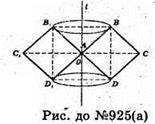
Точка C описує коло радіуса АС. 2π × АС = 8π; AC = 4 см.
AB – сторона квадрата;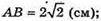 
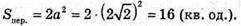
Б)
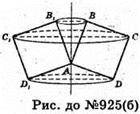
Нехай вісь обертання l утворює зі стороною AB кут 15°, тоді ∠B1AB = 30°.
926.
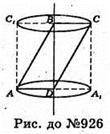
Фігура, утворена при обертанні паралелограма навколо його діагоналі.
927.
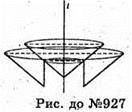
Фігура, утворена обертанням W-подібної ламаної з чотирьох рівних ланок навколо її крайньої ланки.
928.
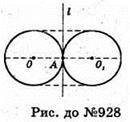
Фігура, утворена обертанням кола навколо його дотичної.
929.
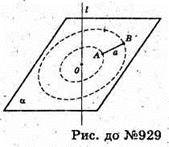
Відрізок AB = а і пряма І не лежать в одній площині.
Відрізок AB = а обертається навколо прямої l.
930.
А)
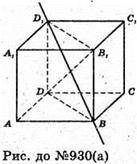
Куб обертається навколо діагоналі. Осьовий переріз;
Б)
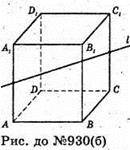
Куб обертається навколо прямої, яка з’єднує середини протилежних ребер.
(1 votes, average: 5.00 out of 5)
Loading...