Геометричні тіла
628.
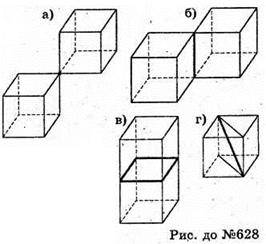
А) спільна вершина;
Б) спільне ребро;
В) спільна грань;
Г) спільна діагональ.
629.
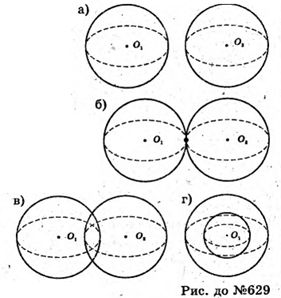
А) дві кулі не мають спільних точок;
Б) дві кулі мають одну спільну точку;
В) дві кулі, які перетинаються;
Г) кулі мають різні радіуси і спільний центр.
630.
Дано точку О і r > 0, г – відстань.
ОХ ≤ r.
Множина всіх точок х простору, які задовольняють умову ОХ ≤ г є кулею.
631.
A) x2 + y2 + z2 = R2-сфера;
Б) х2 + у2 + z2≤ R2 – куля;
В) x2 + y2 + z2 < R2- внутрішня область кулі.
632.
А)
Б) х2 + у2 + z2 ≤ 4 – куля – геометричне тіло;
В) х2 + у2 + z2 < 4 – внутрішня область.
633.
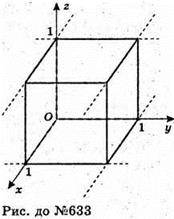
Ця фігура є тілом.
634.
Це не є просторова область.
635.
Ця фігура є просторовою областю. Точка кулі, найближча до точки А, існує.
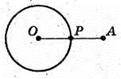
636.
Р – найближча точка до точки А.
637.
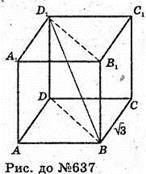
Нехай дано куб ABCDA1B1C1lD1, ребро якого дорівнює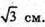 
BD1 – діагональ куба. BD12 = а2 + а2 + а1 = 3а2.
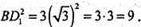BD1 = 3.
Відповідь: 3 см.
638.
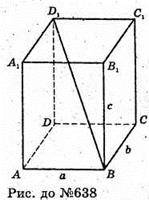
Нехай
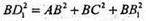
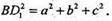
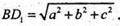
Відповідь: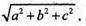 
639.
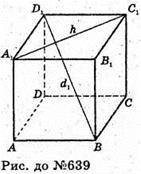
Нехай дано куб, ребро куба дорівнює а, відстань між опорними паралельними площинами дорівнює h.
B1D1 = h.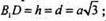 
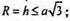
BD1 = d. d2= а2 + а2 +а2; d2 = 3a2;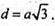 
640.
А) відстань між паралельними опорними площинами до кулі d = 10 см.
(х – 1)2 + (y + 3)2 + (z – 2)2 ≤ 25 × Rкулі = 5см.
R – радіус кулі з центром O(1; -3; 2);
Б) z2 + x2 + y2 – 2x + 2y – 6z ≤ 5.
(x2 – 2x + 1) + y2 + 2y + 1) – 1 – 1 + (z2 – 6z + 9)-9 ≤ 5
(x – 1)2 + (y + 1)2 + (z – 3)2 ≤ 16.
Центр O(1; -1; 3); радіус кулі R = 4 см.
Відстань між паралельними oпорними площинами до кулі: d = 8 см.
641.
(х + 5)2 + (y – 3)2 + (z -1)2 ≤ 1 т. М(-2; 1; 3).
Координати центра O(-5; 3; 1). Відстань від точки М до центра О
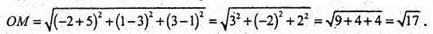
Через точку (-2; 1; 3) опорну площину провести до кулі не можна.
642.
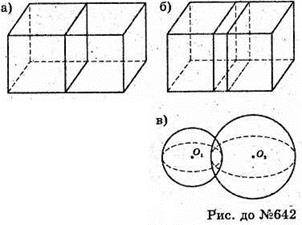
А) об’єднання фігур є тілом;
Б) їх переріз є тілом;
В) об’єднання куль не є тілом;
Г) переріз куль не є тілом.
643.
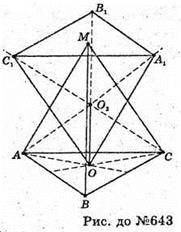
Тетраедр OA1C1B1, симетричний тетраедру МАВС відносно середини його висоти MB. О2 – середина його висоти.
644.
Рівняння І кулі:
(x – 0)2 + (у – 2)2 + (z + 0)2 = 9
X2 +(у – 2)2 + z2 =9 ; R1 = 3.
Рівняння II кулі:
(х – 0)2 + (у – 9)2 + (z – 0)2 = 9; R2 = 3
Х2 +(у-9)2 + 22 = 9.
Знайдемо відстань між центрами куль:·
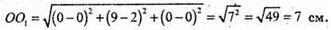
R1 + R2= 6 (см). d = R1 + R2 = 6 (см).
D 1 – відстань між центрами, ОО 1 =7 см.
7 – 6 = 1 (см).
Відповідь: 1 см.
645.
Найближчі точки внутрішніх областей куль, описаних у задачі № 644,
Не існують.
646.
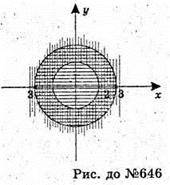
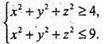
X2 + у2 + z2 ≤ 9 – куля з центром на початку координат і радіусом R = 3.
Фігура, координати точок якої задовольняють систему нерівностей, є тілом.
647.
Знайдемо діаметр тетраедра ОАВС, вершини якого знаходяться в точках:
O(0; 0; 0); А(2; 0; 0); С(0; 0; 2); В(0; 2; 0).
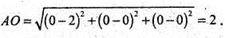
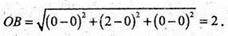
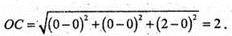
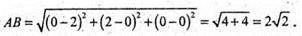
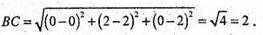
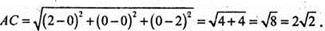
Діаметри: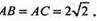 
648.
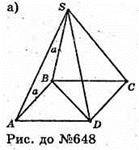
А) нехай дано піраміду SABCD, в основі якої лежить квадрат ABCD, СВ + площині ABCD. SB = АВ = а. BD > AB, BD > ВС > SD > SA, SD > SC.
ΔSBD – прямокутний. ΔBCD – квадрат;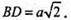 
За теоремою Піфагора: SD2 = SB2 + BD2 = а2 + 2а2 = 2а2.
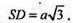SD – діаметр.
Відповідь: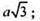 
Б) нехай дано піраміду SABCD, в основі якої ABCD – ромб. ∠ ABC – 120°.
ΔABD – рівносторонній. АВ = AD = BD = а. SD – діаметр.
SD2 = SB2 + BD2. SD2=а2 + а2 = 2а2;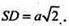 
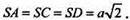
Відповідь: а)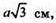 
б) 
649.
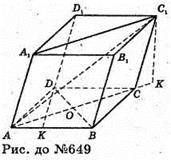
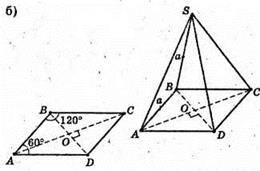
Нехай дано паралелепіпед, усі грані якого рівні ромби зі стороною
АВ = ВС = CD = AD = а і кутом ∠DAB = α.
ΔBCD – ромб. ∠DAB = 60°; Δ ADB – рівностронній.
АВ = AD = а;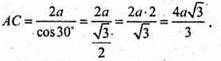 
650.
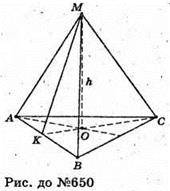
Нехай дано правильний тетраедр, ребро якого дорівнює а
AM = ВМ = CM = АВ = ВС = АС = а.
Відстань між паралельними опорними площинами дорівнює h. МО = h.
OK + АВ; МK + AB.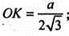 
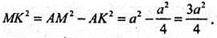
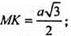
MO2 = МK2 – ОK2;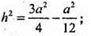 
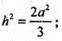
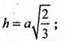
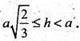
651.
Нехай дано рівняння кулі: х2 + у2 + z2- 2х + 4у ≤ 20 ;
Х2 – 2х + 1 – y + у2 + 4у + 4 – 4 + z2 ≤ 20;
(x2 – 2x + 1) + (y2 + 4y + 4) + z2 ≤ 20 + 1 + 4
(х – 1)2 + (у+ 2)2 + z2≤ 25 .
Радіус кулі R = 5.
Центр кулі 0(1; -2; 0).
Рівняння опорної площини, проведеної до кулі,
(х – 1) 2 + (у + 2)2 + z2 ≤ 25 у точці А(4; -2; 4)
3х + 4z – 28 = 0.
Відповідь: 3х + 4г – 28 = 0.
652.
Нехай дано тетраедр ОАВС, задано координатами вершин O(0; 0; 0); В(0; 3; 0); А(3; 0; 0); С(0; 0; 3). Через грані тетраедра проходять опорні площини.
Рівняння площини АОВ
X1, y1, z1 x2, y2, z2 x3, y3, z3
O(0; 0; 0); А(3; 0; 0); В(0; 3; 0)
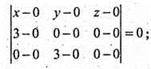
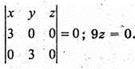
Аналогічно 9х = 0; 9y = 0. Рівняння ABC
X1, y1, z1 x2, y2, z2 x3, y3, z3
А(3; 0; 0); В(0; 3; 0); С(0; 0; 3);
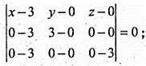
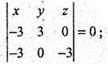
-9х + 9z – 9y = 0;
Х + у – z = 0.
Отже, рівняння опорних площин: z = 0; х = 0; у = 0; х + у – z = 0.
(1 votes, average: 5.00 out of 5)
Loading...