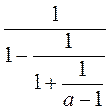Тотожні перетворення раціональних виразів
Урок № 19
Тема. Тотожні перетворення раціональних виразів
Мета: закріпити знання учнів про алгоритми тотожних перетворень раціональних виразів, способи перетворення відношення двох дробових виразів та про схеми застосування властивостей арифметичних дій під час перетворення раціональних виразів.
Тип уроку: корекція знань, відпрацювання навичок.
Наочність та обладнання: опорний конспект “Тотожні перетворення алгебраїчних виразів”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Ретельному
Вираз | Спільний знаменник Чисельника і знаменника | Добуток спільного знаменника на чисельник цього дробу | Добуток спільного знаменника на знаменник даного дробу | Утворений дріб | Дріб, що утворився Після спрощення |
Зрозуміло, що ефективною ця
Для учнів, які добре опанували прийоми роботи з виразами, що виносяться на контроль на ньому етапі уроку, вчитель може запропонувати додаткові завдання саме такого типу та оцінити їх виконання.
III. Формулювання мсти і завдань уроку
Проведена перевірка виконання домашнього завдання та аналіз можливих помилок самі по собі створюють мотивацію учнів до діяльності щодо усунення причини помилок (корекції знань), а також вдосконалення вмінь (формування навичок). Досягнення найкращих результатів цієї діяльності – корекція знань та відпрацювання вмінь учнів виконувати перетворення раціональних виразів із застосуванням вивчених алгоритмів виконання арифметичних дій із раціональними дробами – і складає основну дидактичну мсту уроку.
IV. Актуалізація опорних знань та вмінь
@ З метою успішного сприйняття учнями навчального матеріалу перед вивченням матеріалу уроку слід активізувати такі знання. і вміння учнів: правила виконання арифметичних дій із раціональними числами та порядок виконання дій у числових виразах, що містять дії різного ступеня; тотожні перетворення цілих виразів; перетворення суми, різниці, добутку й частки двох раціональних дробів на раціональний дріб, а також перетворення раціонального дробу із застосуванням основної властивості раціонального дробу (зведення раціонального дробу до нового знаменника, зведення кількох раціональних дробів до нового найменшого спільного знаменника).
Враховуючи дидактичну мету (наголос на корекційній роботі) та з метою урізноманітнення форм роботи на уроці, можна запропонувати учням на цьому етані уроку провести бліцопитування (або провести інтерактивну вправу “Мікрофон”); головна умова – чітка і коротка відповідь на запитання.
Запитання
1. Як формулюється основна властивість дробу?
2. Що відбудеться зі знаком дробу, якщо замінити знак його чисельника; знаменника; чисельника і знаменника?
3. Як додати дроби з однаковими знаменниками?
4. Як виконати віднімання дробів з однаковими знаменниками?
5. Як додати дроби з різними знаменниками? Розкажіть на прикладі дробів: а) 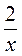 і
і 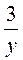 ; б)
; б) 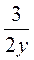 і
і 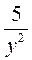 .
.
6. Як виконати множення двох дробів?
7. Яке, ви знаєте правило піднесення дробу до степеня?
8. Сформулюйте правило ділення дробів.
9. Розкажіть про порядок перетворення виразів: а) 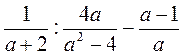 ; б)
; б) 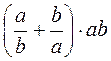 ; в)
; в) 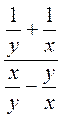 .
.
V. Формування вмінь
Виконання усних вправ
1. Подайте у вигляді нескоротного дробу вираз:
А) 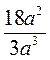 ; б)
; б) 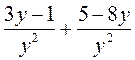 ; в)
; в) 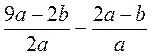 ; г)
; г) 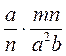 ; д)
; д) 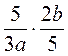 ; є)
; є) 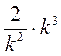 ; ж)
; ж) 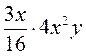 ; з)
; з) 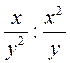 ; и)
; и) 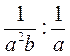 ; к)
; к) 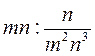 ; л)
; л) 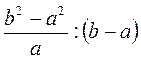 .
.
2. Назвіть найменший спільний знаменник дробів (виразів):
А) 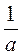 і
і 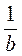 ; б) а;
; б) а; 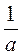 і
і 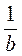 ; в)
; в) 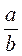 ;
; 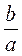 і
і 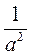 ; г)
; г) 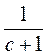 і
і 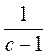 .
.
3. При яких значеннях змінної значення дробу дорівнює нулю?
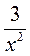 ;
; 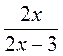 ;
; 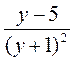 ;
; 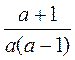 ;
; 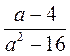 .
.
Виконання письмових вправ
На уроці корекції знань та відпрацювання навичок логічно буде запропонувати учням розв’язати вправи приблизно такого змісту:
1. Перетворення раціонального виразу на раціональний дріб (за загальною схемою, складеною на уроці 17).
1) Спростіть вираз: а) 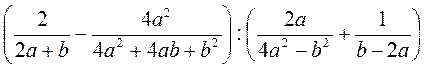 ; б)
; б) 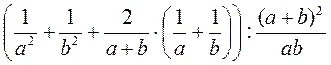 ; в)
; в) 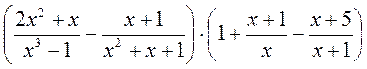 .
.
2) Спростіть вираз: а) 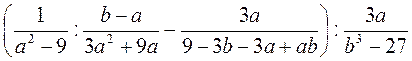 ; б)
; б) 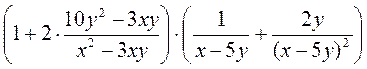 ; в)
; в) 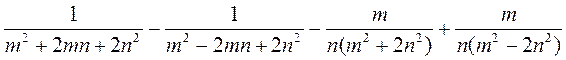 .
.
3) Спростіть вираз:
а) 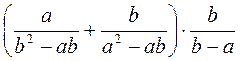 ; б)
; б) 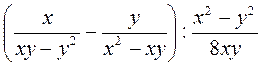 ; в)
; в) 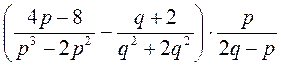 ; г)
; г) 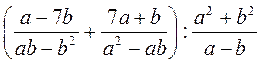 .
.
4) Виконайте дії:
а) 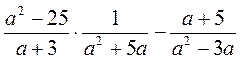 ; б)
; б) 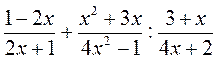 ; в)
; в) 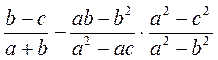 ; г)
; г) 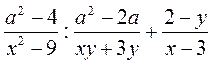 .
.
5) Спростіть вираз:
а) 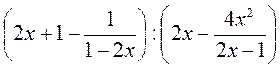 ; б)
; б) 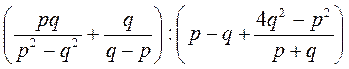 ; в)
; в) 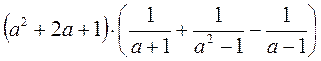 ;
;
Г) 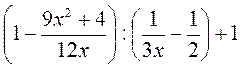 ; д)
; д) 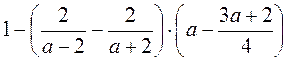 ; є)
; є) 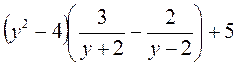 .
.
2. Подання відношення дробових раціональних виразів у вигляді відношення многочленів (із застосуванням основної властивості дробу).
1) Подайте у вигляді раціонального дробу: 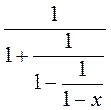 .
.
2) Знайдіть значення виразу:
А) 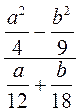 при а =
при а = 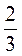 , b =
, b = 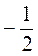 ; б)
; б) 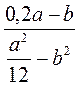 При а = -8, b = 0,6.
При а = -8, b = 0,6.
3) Подайте у вигляді раціонального дробу:
А) 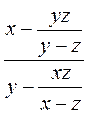 ; б)
; б) 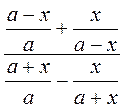 ; в)
; в) 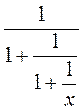 ; г)
; г)  .
.
3. Доведення того, що значення виразу не залежить від значення змінної.
1) Доведіть, що при всіх допустимих значеннях букв значення виразу 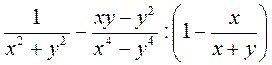 дорівнює 0.
дорівнює 0.
2) Доведіть, що при будь-якому натуральному n значення виразу 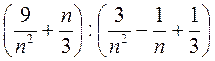 є натуральним числом.
є натуральним числом.
4. Доведення тотожностей.
Доведіть тотожність:
А) 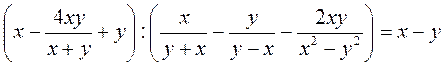 ;
;
Б) 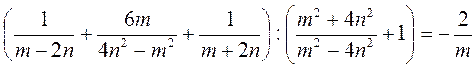 .
.
5. Вправи на повторення (особливо на знаходження ОДЗ раціонального виразу та відшукання значення змінних, при яких значення виразу дорівнює нулю).
6. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Подайте у вигляді раціонального дробу вираз: а) 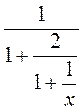 ; б)
; б) 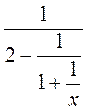 .
.
2) Доведіть, що при всіх допустимих значеннях змінних значення виразу: 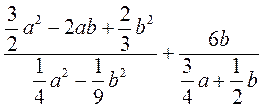 не залежить від а і b.
не залежить від а і b.
3) Який вираз пропущено?
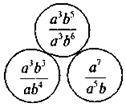


@ Як було сказано вище, завдання на перетворення раціональних виразів на раціональний дріб у загальному випадку є досить складним завданням, бо передбачає вільне оволодіння алгоритмами виконання різних арифметичних дій із раціональними дробами, а також достатньо високий рівень умінь застосовувати ці алгоритми на практиці та переключатись з одного алгоритму на інший. Тому рівень складності завдань учитель вибирає залежно від рівня знань та вмінь учнів, не занижуючи вимоги до учнів, але водночас створюючи ситуацію успіху. З метою підготовки учнів до сприйняття наступного розділу (“Раціональні рівняння”) слід продовжити розв’язувати вправи на знаходження ОДЗ раціонального виразу та відшукання значення змінних, при яких значення виразу дорівнює нулю.
VI. Підсумки уроку
Самостійна робота № 5
Варіант 1 | Варіант 2 |
Виконайте дії: | |
А) Б) В) Г) | А) Б) В) Г) |
VII. Домашнє завдання
1. Повторити алгоритми виконання арифметичних дій із раціональними дробами.
2. Розв’язати вправи змісту, аналогічного вправам самостійної роботи (можна запропонувати вправи протилежного варіанта).
3. Повторити: означення раціонального, цілого раціонального і дробового раціонального виразів, ОДЗ раціонального виразу; означення рівняння, властивості рівносильності рівнянь, поняття лінійного рівняння з однією змінною та алгоритм розв’язання лінійного рівняння; розв’язати лінійні рівняння (у тому числі й рівняння з параметрами); повторити зміст поняття “пропорція” та основну властивість пропорції, розв’язати кілька рівнянь на застосування цієї властивості (див. 6 клас).
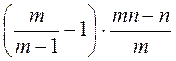 ;
;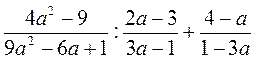 ;
;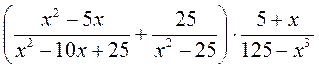 ;
;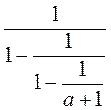
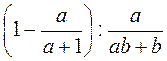 ;
;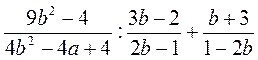 ;
;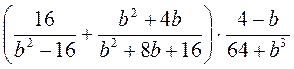 ;
;