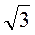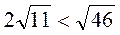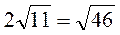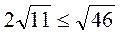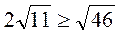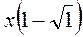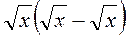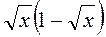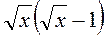Тотожні перетворення виразів, що містять квадратний корінь
Урок № 43
Тема. Тотожні перетворення виразів, що містять квадратний корінь
Мета: поглибити знання учнів відомостями про способи перетворення дробових виразів, що містять квадратні корені; сформувати вміння застосовувати вивчені способи дій для перетворення дробових виразів, що містять квадратні корені, у завданнях, передбачених програмою з математики.
Тип уроку: застосування знань, умінь та навичок.
Наочність та обладнання: опорний конспект “Перетворення ірраціональних виразів”.
Хід уроку
I. Організаційний етап
II.
Рівень засвоєння учнями знань та вмінь попереднього уроку можна визначити під час перевірки домашнього завдання за зразком або проведенням тестової роботи.
Тестова робота 8
Перетворення ірраціональних виразів
1. Спростіть вираз 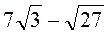 .
.
А | Б | В | Г |
4 | 4 | 61 | 16 |
2. Обчисліть: 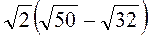 .
.
А | Б | В | Г |
2 | 9 | 18 |
3. Чому дорівнює значення виразу 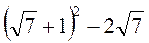 ?
?
А | Б | В | Г |
6 | 48 | 50 | 8 |
4. Порівняйте числа 2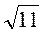 і
і 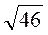 .
.
А | Б | В | Г |
|
|
|
|
5. Розкладіть на множники вираз 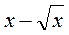 .
.
А | Б | В | Г |
|
|
|
|
III. Формулювання мсти і завдань уроку
З метою створення мотивації учнів до навчальної діяльності на уроці пропонуємо їм виконати завдання, зміст яких відповідає якому-небудь виду тотожних перетворень дробових ірраціональних виразів (наприклад, скоротити дріб 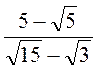 тощо). Спроби виконати перетворення, спираючись тільки на вивчені тотожності та означення арифметичного квадратного кореня, мають переконати учнів у тому, що, крім вивченої теорії з теми “Арифметичний квадратний корінь”, необхідно опанувати способи дій з перетворення не тільки цілих, але й дробових виразів, що містять арифметичний квадратний корінь.
тощо). Спроби виконати перетворення, спираючись тільки на вивчені тотожності та означення арифметичного квадратного кореня, мають переконати учнів у тому, що, крім вивченої теорії з теми “Арифметичний квадратний корінь”, необхідно опанувати способи дій з перетворення не тільки цілих, але й дробових виразів, що містять арифметичний квадратний корінь.
Сформульована проблема – необхідність вивчення спеціальних способів перетворень дробових виразів, що містять квадратний корінь – виражає основну дидактичну мету уроку.
IV. Актуалізація опорних знань та вмінь
@ З метою успішного сприйняття навчального матеріалу слід активізувати такі знання і вміння учнів: виконання арифметичних дій з раціональними числами; виконання тотожних перетворень дробових та цілих раціональних виразів; тотожні перетворення найпростіших цілих виразів, що містять квадратні корені.
Виконання усних вправ
1. Обчисліть: 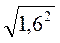 ;
; 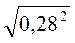 ; 5
; 5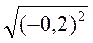 ;
; 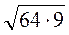 ;
; 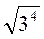 ;
; 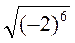 .
.
2. Порівняйте значення виразів: 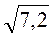 і
і 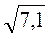 ;
; 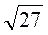 і 6; 0 і
і 6; 0 і 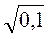 ; 1 і
; 1 і 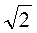 ;
; 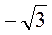 і – 2; х і
і – 2; х і 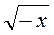 .
.
3. Винесіть множник з-під знака кореня: 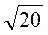 ;
; 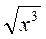 ;
; 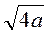 ;
; 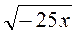 ;
; 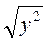 При у? 0;
При у? 0; 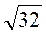 ;
; 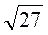 ;
; 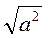 при а? 0;
при а? 0; 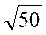 ;
; 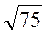 ;
; 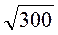 ;
; 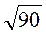 .
.
4. Внесіть множник під знак кореня: 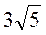 ;
; 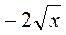 ;
; 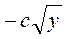 при с > 0;
при с > 0; 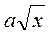 при а < 0.
при а < 0.
5. Розкладіть на множники: а) ах + х; б) 3х2 – х; в) 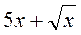 ; г)
; г) 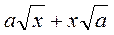 ; д) а2х2 – 1; е) (а + х)2 – 1; ж) 49 + х2 – 14х; з) 3а3 – 27а.
; д) а2х2 – 1; е) (а + х)2 – 1; ж) 49 + х2 – 14х; з) 3а3 – 27а.
V. Застосування знань
@ Так само як і на попередньому, на цьому уроці не вивчаються нові теоретичні положення: весь зміст нового матеріалу представлений опорними прикладами виконання завдань на перетворення дробових виразів, що містять арифметичний квадратний корінь. Тому план вивчення матеріалу уроку являє собою фактично опис змісту виразів, способи перетворення яких мають опанувати учні.
1. Скорочення дробів, що містять квадратні корені.
Скоротіть дріб: а) 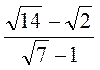 ; б)
; б) 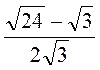 ; в)
; в) 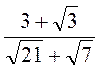 ; г)
; г) 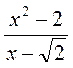 ; д)
; д) 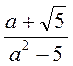 ; є)
; є) 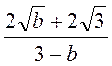 .
.
2. Спрощення виразів, що мають вигляд суми або різниці дробів і містять квадратні корені.
Спростіть вираз: а) 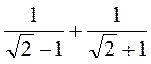 ; б)
; б) 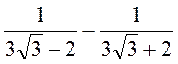 ; в)
; в) 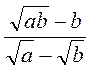 ; г)
; г) 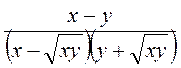 (х > 0, у > 0).
(х > 0, у > 0).
3. (додатково). Спрощення виразів, що мають вигляд складного кореня або суми, різниці, добутку складних коренів.
1) Доведіть, що: а) 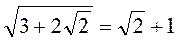 ; б)
; б) 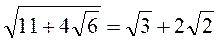 .
.
2) Спростіть вираз: а) 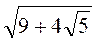 ; б)
; б) 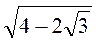 ; в)
; в) 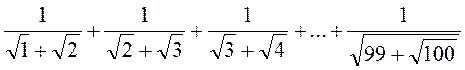 ; г)
; г) 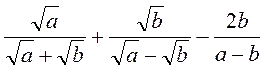 ; д)
; д) 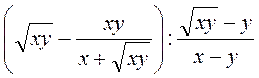 (х > 0, у > 0).
(х > 0, у > 0).
4. Звільнення від ірраціональності в знаменнику дробу.
1) Звільніться від ірраціональності у знаменнику (чисельнику) дробу: а) 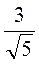 ; б)
; б) 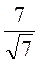 ; в)
; в) 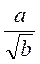 ; г)
; г) 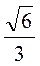 .
.
2) Звільніться від ірраціональності у знаменнику (чисельнику) дробу: а) 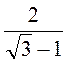 ; б)
; б) 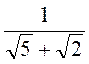 ; в)
; в) 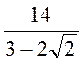 ; г)
; г) 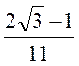 ; д)
; д) 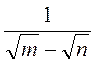 ; є)
; є) 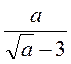 ; ж)
; ж) 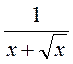 ; з)
; з) 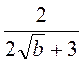 .
.
Слід зауважити, що під час коментування розв’язання типових прикладів (які складають основний зміст навчального матеріалу уроку), вчитель має акцентувати увагу учнів на тому факті, що в перетворенні дробових ірраціональних виразів використовують міркування, аналогічні до тих, що використовувались під час перетворення дробових раціональних виразів.
Принципово новими для учнів є перетворення, що мають назву позбавлення (звільнення) від ірраціональності в чисельнику або знаменнику дробу (традиційно вивчається позбавлення від ірраціональності в знаменнику дробу). Перед вивченням схеми перетворень корисно було б вивчити питання про те. як перетворити добуток кореня на раціональне число в раціональний вираз, а також про перетворення суми або різниці коренів із чисел у раціональне число (для підготовки до сприйняття матеріалу, пов’язаного з позбавленням від ірраціональності в знаменнику дробу, корисно було б виконати відповідні завдання на попередньому уроці під час опрацювання питання про способи перетворень цілих ірраціональних виразів – див. попередній урок). Після опрацювання нього питання звертаємо увагу учнів на те, що основна властивість дробу виконується і у випадку ірраціональних дробів, тому в результаті множення чисельника і знаменника ірраціонального дробу на одне й те саме число, відмінне від нуля, числове значення дробу не зміниться – зміниться лише його вигляд: знаменник дробу перетвориться на раціональний вираз.
VI. Формування вмінь
Виконання усних вправ
1. Розкладіть на множники: а) 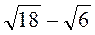 ; б)
; б) 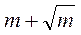 ; в) а – b, де а > 0; b > 0.
; в) а – b, де а > 0; b > 0.
2. Прокоментуйте виконані дії:
А) 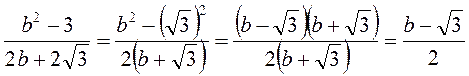 ; б)
; б) 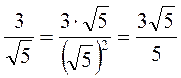 ; в)
; в) 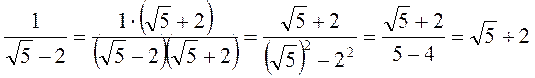 .
.
Виконання письмових вправ
Для реалізації дидактичної мсти уроку на цьому уроці слід розв’язати завдання змісту аналогічного до змісту опорних вправ (див. вище), а також за наявності часу розв’язати вправи:
1. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
Вставте пропущений вираз:
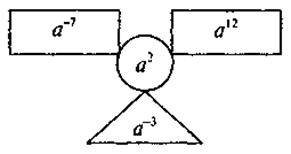
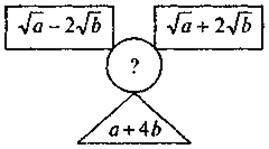
2. На повторення: завдання па перетворення цілих ірраціональних виразів; розв’язування рівнянь.
VII. Підсумки уроку
В якому з випадків правильно виконано дію?
1) 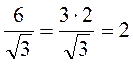 ; 2)
; 2) 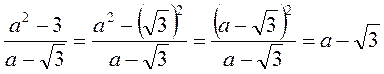 ; 3)
; 3) 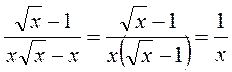 .
.
VIII. Домашнє завдання
1. Вивчити схеми виконання розглянутих на уроці дій із дробовими виразами, що містять квадратні корені.
2. Розв’язати вправи на застосування вивчених схем дій.
3. На повторення: завдання на перетворення цілих ірраціональних виразів.