Третій принцип термодинаміки. Від’ємні температури
ФІЗИКА
Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА
Розділ 7 ОСНОВИ ТЕРМОДИНАМІКИ
7.12. Третій принцип термодинаміки. Від’ємні температури
У 1906 р. принципи термодинаміки було доповнено тепловою теоремою Нернста. Ця теорема не випливає з першого і другого принципів, а виражає новий закон природи, тому її часто називають третім принципом термодинаміки. Суть його полягає в тому, що при абсолютному нулі температур будь-які зміни стану відбуваються без зміни ентропії, або нульова ізотерма збігається з нульовою адіабатою. Адже при
Теорема Нернста приводить до висновку, що не можна досягнути температури абсолютного нуля. За допомогою сучасної техніки можна одержати низькі температури близько 10~5 К. Недосяжність абсолютного нуля температури приводить лише до неможливості переходу від додатних до від’ємних абсолютних температур. Проте теорема Нернста не виключає можливості існування поряд із додатними від’ємних
Якщо виходити з того, що температура пропорційна середній кінетичній енергії частинок, то для атомних систем, яким властива лише кінетична енергія руху частинок, від’ємна температура не має фізичного змісту. Крім молекулярно-кінетичного тлумачення температури її розглядають як величину, що визначає розподіл частинок за енергіями. Якщо скористатися цим більш загальним питанням температури, то дійдемо висновку про існування і від’ємних температур.
Якщо газ перебуває в якомусь силовому полі, а отже, його частинкам властива деяка потенціальна енергія, то кількість частинок, що мають певну енергію 17, визначають за формулою

Вираз (7.37) називають формулою Больцмана. За допомогою цієї формули можна визначити відносну кількість частинок, що мають в умовах теплової рівноваги енергію U:

Із формули (7.38) видно, що відносна кількість n / n0 частинок з енергією U залежить не лише від цієї енергії, а й від температури. Тому температуру використовують як величину, що зумовлює розподіл частинок за енергіями. З формули (7.38) видно, що чим більша U, тим менша відносна кількість частинок n / n0, які мають цю енергію. Зрозуміло, що в рівноважному стані, для якого справедливий закон Больцмана, n завжди менше від n0. Логарифмуючи рівність (7.38), дістанемо

Звідки

Отже, якщо n < n0, то Т > 0. Для атомної системи, в якій n може бути і більшим за n0, температура може бути також від’ємною, оскільки при n > n0 Т стає від’ємною.
Умови реалізації такого випадку легше зрозуміти, якщо розглянути не класичну систему, де від’ємна температура не може бути реалізована, а квантову і скористатися поняттям ентропії, що визначає ступінь хаосу в системі.
При абсолютному нулі температур усі частинки системи перебувають на своїх звичайних енергетичних рівнях, а всі інші рівні порожні. Система в таких умовах максимально впорядкована, і її ентропія дорівнює нулю (дорівнює нулю і її теплоємність).
У разі збільшення температури системи наданням їй енергії частинки переходитимуть також на вищі рівні енергії. При цьому чим вища температура, тим більша “населеність” більш високих енергетичних рівнів. Розподіл частинок на енергетичних рівнях визначають за формулою Больцмана (7.37). “Розселення” частинок на багатьох рівнях збільшує, звичайно, хаос у системі, і ентропія її зростає з підвищенням температури. Найбільший хаос, а отже, і максимум ентропії відповідали б такому розподілу частинок за енергіями, коли вони рівномірно розподілялись на всіх енергетичних рівнях. Такий розподіл означав би, що у формулі (7.37) n = n0 і, отже, Т = ∞. Таким чином, рівномірний розподіл частинок за енергіями відповідає нескінченно високій температурі та максимальній ентропії.
Якщо надати системі, що вже перебуває при нескінченно високій температурі, додаткову енергію, то частинки змушені будуть підніматися на більш високі енергетичні рівні, а це приведе до того, що “заселеність” цих рівнів буде більшою від найнижчого рівня. Таке переважне накопичення частинок на більш високих рівнях відповідає вже деякому впорядкуванню порівняно з тим повним хаосом, який був при Т = ∞, тобто при рівномірному розподілі частинок за енергіями. Ентропія, що досягає максимуму при T = ∞, починає зменшуватися при подальшому наданні системі енергії. Проте якщо зі зростанням енергії ентропія системи не збільшується, а зменшується, то це означає, що температура її не додатна, а від’ємна.
Чим більша енергія підводиться до системи, тим більше частинок опиниться на найвищих енергетичних рівнях. У граничному випадку можна уявити стан, коли всі частинки зберуться на найвищих рівнях. Такий стан, очевидно, є також повністю впорядкованим, і ентропія його дорівнює нулю. Тому температуру, за якої встановлюється цей повністю впорядкований стан, позначають через -0, на відміну від звичайного абсолютного нуля (+0) (рис. 7.7).
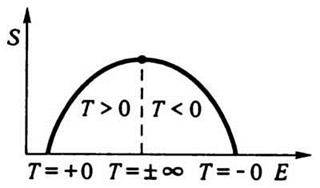
Рис. 7.7
Відмінність між цими двома нулями полягає в тому, що до першого з них ми підходимо з боку від’ємних, а до другого – з боку додатних температур.
Отже, можливі температури системи не обмежуються інтервалом від абсолютного нуля до нескінченності, а поширюються від +0 до +∞, від -∞ до -0, до того ж +∞ і -∞ збігаються одна з одною. З погляду впорядкованості, а отже, і ентропії можливі такі три стани:
1. Повне впорядкування – частинки сконцентровані на найнижчих рівнях енергії. Цей стан відповідає “звичайному” абсолютному нулю температур (+0).
2. Повний хаос – частинки рівномірно розподілені на всіх енергетичних рівнях. Цьому станові відповідає температура ±∞.
3. Повне впорядкування – частинки займають лише найвищі енергетичні рівні. Температурі, що відповідає цьому стану, приписують значення -0.
Існує дуже важлива відмінність між цими двома впорядкованими станами з температурами +0 і -0. Стан “звичайного” абсолютного нуля, якщо його можна було б створити в системі, є станом стійкої рівноваги, з якого система сама по собі, без втручання ззовні, не може вийти. Це пов’язано з тим, що енергія системи в такому стані набуває мінімального значення.
Стан негативного абсолютного нуля є станом надто нерівноважним, оскільки в цьому разі енергія системи максимальна. Якщо можна було б привести систему в такий стан, а потім залишити її саму на себе, то вона відразу вийшла б з цього нерівноважного, нестійкого стану. Його можна було б зберегти, тільки неперервно надаючи системі енергію. Без цього частинки, що розміщуються на вищих енергетичних рівнях, обов’язково переходитимуть на нижчі рівні.
Загальною властивістю обох “нулів” є недосяжність їх: для досягнення їх треба затратити нескінченно велику енергію.
Нестійким, нерівноважним є не тільки стан, що відповідає температурі -0, а й усі стани з від’ємними температурами. Всім їм відповідають значення n > n0, а для рівноваги потрібне протилежне співвідношення n та n0 (n < n0).
Слід зазначити, що атомні системи, в яких можливі стани з від’ємними температурами, – це не тільки уявна теоретична побудова. Такі системи реально існують, і в них можна здійснити від’ємні температури. Випромінювання, що виникає при переході зі стану з від’ємною в стан зі звичайною температурою, практично використовують у спеціальних приладах – молекулярних генераторах і підсилювачах (мазерах та лазерах), про які йтиметься в підрозділі 15.13.