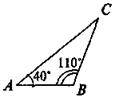
Трикутник і його види
Урок 40
Тема. Трикутник і його види
Мета: подальше закріплення знань учнями класифікації трикутників, доповнення їх алгоритмами побудови трикутників за двома сторонами і кутом між ними та за стороною і прилеглими кутами; формування вмінь розв’язування задач на побудову і вдосконалення вмінь розв’язувати задачі на обчислення периметрів прямокутника, квадрата і трикутника.
Тип уроку: застосування знань, умінь, навичок.
Хід уроку
І. Перевірка домашнього завдання
Запитання до класу
1. Назвіть вид трикутника (рис.
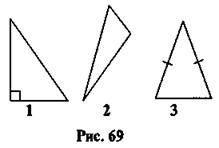
2. Який вигляд має трикутник зі сторонами 14 см, 17 см і 17 см? Як скласти вираз для обчислення його периметра? [Рівнобедрений, основа – 14 см, бічна сторона – 17 см,
Р = 217 + 14 = 48 (см).]
3. І ст. – 12 (см)
ІІ ст. – 3 – 12(см)
III ст. – 3 – 12 – 8 (см)
Як описати словами залежність між сторонами трикутника?
Що являє собою значення виразу 12+3 12+(3 12-8)=76 (см)?
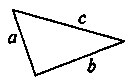
4. Р = а + b + с
С = Р – (а + b) = Р – а – с
Знайдіть значення с, якщо Р = 9 см; а = 3 см; 6=4 см.
II. Доповнення знань
Мотивація навчальної діяльності
У ч и т е л ь. На попередньому уроці ми з’ясували, як можна класифікувати (поділяти на види) трикутники і інші об’єкти. Ми також навчились креслити трикутники певного виду (рівнобедрені, прямокутні тощо).
Як побудувати трикутник не просто певного виду, а щоб сторони мали певну довжину, а кути (кут) певну градусну міру?
Побудова трикутників
На цьому етапі доречно організувати роботу учнів з підручником. Після розбору прикладів 1 і 2 (с. 98-99) зробити такі самі побудови в зошитах. Записи в зошитах можуть мати такий вигляд:
Приклад 1 | Приклад 2 | ||
|
АС = 4 см АВ = 2 см
|
| АС = 8 см
|
Після цього, проаналізувавши побудову, доходимо висновку, що:
1) за двома сторонами і кутом між ними побудову трикутника виконують у такому порядку: будуємо кут; на його сторонах відкладаємо 2 відрізки відомої довжини;
2) за стороною і двома прилеглими до неї кутами побудову трикутника виконують у такому порядку: будуємо сторону; від неї відкладаємо 2 кути.
III. Закріплення матеріалу
№ 376 (1-6). Побудова трикутників за двома сторонами і кутом між ними та за стороною і прилеглими до неї кутами.
№ 365. Побудова трикутника, вимірювання відрізків і кутів, обчислення периметра трикутника.
Додатково: № 430 – на обчислення периметра трикутника. № 378 – на розвиток просторової уяви учнів.
IV. Домашнє завдання
П. 14, № 377; 373; 367; повторити п. 10,392 (4) на розв’язування рівнянь.
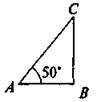
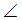 A = 50°
A = 50°