Величини. Площа геометричних фігур
Величини. Площа геометричних фігур
215. Розгляньте малюнок. Подумайте й скажіть, на якій поверхні кожної з парт можна розмістити більше предметів. Поясніть свою думку.

– Розгляньте малюнки. Спробуйте намалювати поверхні цих предметів у зошиті й порівняти кожну пару.

– Чи правильне твердження, що поверхня кожного з предметів має форму геометричної фігури – прямокутника чи круга?
216. Розгляньте відрізки. Порівняйте їх довжини. Який відрізок довший, а який – коротший?

Олена запропонувала порівняти відрізки способом накладання відрізка АВ на відрізок CD.
Поліна запропонувала виміряти довжину кожного відрізка й порівняти одержані числові дані, щоб установити різницю між відрізками АВ та CD.
– Чи можна таким способом порівняти смужки А і С?

Сергій вважає, що порівняти таким способом смужки не можна. Краще скористатися способом накладання смужки С на смужку А, щоб побачити, що вони не рівні. У такому випадку кажуть: площа смужки С менша від площі смужки А (чи: площа смужки А більша
Площа – це величина, яку можна виміряти.
Позначається площа фігур латинською буквою S.
217. Розгляньте геометричні фігури. Чим вони подібні, а чим відрізняються?
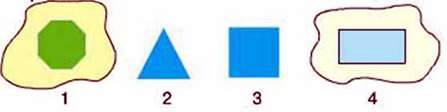
– Чи правильне твердження, що фігури 1 та 4 розміщені на площині та мають площу?
– Визначте, за якою ознакою фігури розділили на 2 групи.
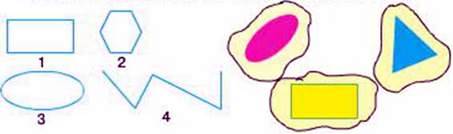
– Випишіть фігури, які можуть бути межею фігур, що мають площу.
– Ни правильне твердження, що площа – це частина площини, яка обмежена замкненою лінією? Поясніть свою думку.
218. Перший в Україні трамвай вийшов на маршрут у Києві 1892 року. Скільки років у нашій країні працює цей вид транспорту?

219. Із 10 метрів тканини пошили 3 дитячих підодіяльники. Скільки підодіяльників можна пошити із сувою тканини 303 м та сувою 317 м?
– Скільки підодіяльників можна пошити із тканини, що є в цих двох сувоях разом?
Учні записали свої відповіді на друге запитання задачі так:
Катя. 186 (п.); Нікіта: 183 (п.).
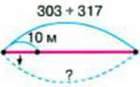
– Поясніть, як міркували діти. Хто з них вірно розв’язав задачу?

220. Обчисліть.
125 : 25 + 75 : 5; 1919 – 47 ∙ 35 + 349; 244 : 61 + 275 : 55.
Виконайте вдома
221. Обчисліть.
65 ∙ 17 – 16 ∙ 42 100 : 25 + 354 : 59
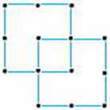
222. Фігуру складено з 16 паличок. Перекладіть 4 палички так, щоб утворилося 4 рівних квадрати.
223. Діти вимірювали площі фігур різними мірками:
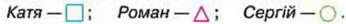
– Яка з мірок дала змогу найточніше визначити площу фігури?

Вероніка обчислювала площу фігури за допомогою всіх мірок і отримала такі результати:

– Оберіть правильну відповідь. Поясніть свій вибір.
224. Учень із прозорого паперу виготовив палетку, розділив її на квадрати зі стороною 1 см. Наклав палетку на фігури К, С, Д та записав результати вимірювання площі кожної фігури.
Фігура К має площу 6 см2. Фігура С має площу 12 см2. Фігура Д має площу 22 см2.
– Перевірте, чи правильно учень визначив площу фігур.
Квадрат зі стороною 1 см називається квадратним сантиметром і позначається так: 1 кв. см, 1 см2.
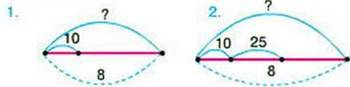
225. Одна секретарка друкує за годину 10 сторінок, а інша – 25 сторінок. Скільки сторінок вони надрукують за 8 годин, якщо працюватимуть разом?
– Розгляньте схеми. Оберіть схему до задачі та розв’яжіть її за цією схемою.
226. Обчисліть.
195 : 65 + 40 ∙ 2 : 100 78 ∙ 84 + 520 – 4078
227. Запишіть числа о порядку їх зменшення.
25 634; 26 890; 26 782; 29 647; 29 463.
Виконайте вдома
228. У 4 коробках на 21 кг печива менше, ніж у 7 таких самих коробках. Скільки кілограмів печива в одній коробці?
– Накресліть схему. Розв’яжіть задачу.
229. Знайдіть значення виразів
(540 – 324) : 27 + 312 600 – 40 ∙ 10 + 724
230. Фігуру складено з 10 сірників. Перекладіть 3 сірники так, щоб утворилося 2 нерівних квадрати.

231. Діти обчислювали площу фігури ABCD, довжина якої 6 см, а ширина – 3 см.
Віка використала палетку й записала відповідь: площа фігури становить 18 кв. см.
Сергій поділив фігуру на мірки – по 1 кв. см і запропонував підрахувати кількість квадратів у одному рядку, щоб дізнатися, скільки сантиметрів становить довжина прямокутника. А кількість таких рядків вказує на його ширину. Щоб вирахувати площу фігури, треба 6 взяти 3 рази: 6 см х 3 см = 18 (кв. см).
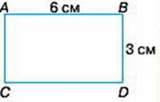

Відповідь: площа фігури становить 18 кв. см.
Оксана міркувала так: якщо ширина прямокутника становить 3 см, тоді в стовпчику поміститься 3 квадрати, а оскільки ширина фігури 6 см, таких стовпчиків буде 6. Тобто по 3 взяти 6 разів: 3 см ∙ 6 см = 18 (кв. см).
Відповідь: площа фігури становить 18 кв. см.
– Подумайте й скажіть, хто з дітей зробив обчислення правильно.
– Чи можливі квадрат із довжиною сторони 1 дм; 1 м? Поясніть свої міркування.
Запам’ятайте!
Для вимірювання площі геометричних фігур математики обрали найзручніші мірки:
– площа квадрата зі стороною 1 см = 1 кв. см = 1 см2;
– площа квадрата зі стороною 1 дм = 1 кв. дм = 1 дм2;
– площа квадрата зі стороною 1 м = 1 кв. м =1 м2
232. Запишіть мірки, якими вимірюємо такі величини:
1. площа кімнати становить 35 □;
2. площа столу – 72 □;
3. площа першої сторінки обкладинки підручника становить 600 □.
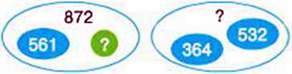
233. Розгляньте малюнки, на яких зображені дві множини чисел. Запишіть рівності до кожної із множин і назвіть її компоненти.
234. На перший склад завезли 560 кг солі, а на другий – на 460 кг більше. З кожного зі складів солі продали по 400 кг. Де солі залишилося більше і на скільки?
– Накресліть схему до умови задачі.
– Поміркуйте, чи можна дати відповідь на запитання задачі, не розв’язуючи її.
Виконайте вдома
235. Катя, Наталка й Оленка гралися в слова. Катя записала на 15 слів більше, ніж Оленка, і на 4 слова більше, ніж Наталка. Скільки всього слів записали дівчата, якщо відомо, що Катя записала 27 слів?
236. Порівняйте вирази, не обчислюючи їх значення.
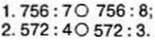
237. Прочитайте хибну рівність. Заберіть 2 палички так, щоб рівність стала істинною.
238. Накресліть прямокутник зі стороною 3 см та 4 см.
– Розділіть його на квадрати Порахуйте їх.
– Подумайте, чи можна побудувати інші прямокутники, площа яких також дорівнює 12 см2 Якщо так, тоді накресліть їх і поділіть на квадратні сантиметри.
239. Розгляньте таблицю. Визначте, як було обчислено дані, що записані в її останньому стовпці. Поясніть свої міркування.
Довжина | Ширина | Площа |
4 см | 3 см | 12 см2 |
6 см | 2 см | 12 см2 |
6дм | 3дм | 18 дм2 |
240. Довжина парти 12 дм, а її ширина – 6 дм. Обчисліть площу парти.
– Чи можна скористатися таким способом обчислення площі, як у попередніх завданнях?
Запам’ятайте!
Площу прямокутника можна визначити, помноживши його довжину (а) на ширину (b).
Площа фігури позначається буквою S.
Sпр. = а ∙ b
241. Обчисліть площі прямокутників

– Побудуйте фігуру, яка має таку саму площу, що й фігура К.
– Обчисліть периметр кожної фігури.
– Знайдіть довжину прямокутника, якщо його ширина 6 см, а периметр 20 см.
Виконайте вдома
242. Ширина прямокутника 6 см, а його довжина у 4 рази більша. Обчисліть площу прямокутника та його периметр.
243. Обчисліть.
(327 – 311) ∙ 12 – (411 – 436).
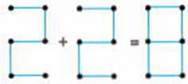
244. Перекладіть 3 сірники так, щоб одержати 5 рівних квадратів
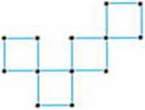
245. Вилучте “зайве”.
1. 3065 см, 456 дм, 7 806 км, 605 м2, 2873 км;
2. 12 м2, 695 см2, 89 дм2, 18 м, 602см2;
3. 1 м2, 10 дм2, 1000 м2, 10 000 см2, 100 дм2.
246. Оберіть зручні мірки для обчислення площі:
1. класної кімнати;
2. класної дошки;
3. учнівського пенала.
Поміркуйте, чи зручно такими мірками вимірювати площу засіяного пшеницею поля?
Запам’ятайте!
Для вимірювання земельних ділянок застосовують інші одиниці вимірювання:
1 ар (1 а) – квадрат, сторона якого дорівнює 10 м (цю одиницю площі часто називають “соткою”, оскільки площа такого квадрата 10 ∙ 10 = 100 м2).
1 гектар (1га) – квадрат, сторона якого дорівнює 100 м2.
247. Поле довжиною 320 м та шириною 60 м засіяли горохом і квасолею. Горохом засіяно 64 а. Решту поля засіяно квасолею. Скільки арів засіяно квасолею?
Олена міркувала так: по довжині ділянки вміститься 32 а – 1 ряд, а таких рядків – 6. Звідси:
S = 32 ∙ 6 = 192 (а).
Площа всього поля 192 а.
Роман спочатку обчислив площу поля так: 320 м ∙ 60 м = 19 200 м2; потім визначив кількість сотень у числі, адже кожна сотня це 1 ар. А оскільки 1 ар = 100 м2, тоді площа поля 19 200 м2: 100 м2 =192 а.
– Продовжте розв’язок задачі. Запишіть відповідь до неї.
248. У зоопарку лев і левиця за 3 дні з’їдають 48 кг свіжого м’яса. Скільки кілограмів свіжого м’яса потрібно одній тварині для повноцінного харчування?
– Розгляньте схему до задачі. Розв’яжіть її.

249. Обчисліть
148 ∙ 37 + (120 -80) : 5; 198 : 28; 472 : 59.
250. Чому дорівнює ширина прямокутника, якщо його довжина в два рази більша за ширину, а периметр 18 см?
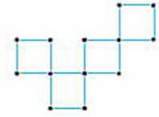
251. Перекладіть 3 палички так, щоб одержати 1 великий і 2 малих квадрати
252. Накресліть прямокутник, довжина якого 10 см. Визначте ширину прямокутника, якщо відомо, що його площа становить 50 см2.
– Розмістіть квадратні сантиметри по довжині прямокутника.
– Скільки таких рядків поміститься у прямокутнику?
– Запишіть рівність на знаходження однієї зі сторін прямокутника.
Запам’ятайте!
Щоб знайти довжину однієї сторони ділянки прямокутної форми, необхідно площу ділянки поділити на довжину другої сторони:
A = S : b
253. Площа кімнати дорівнює 42 м2. Визначте її ширину, якщо відомо, що довжина кімнати дорівнює 7 м.
254. Площа поля, що засіяне просом, пшеницею й житом, становить 840 а. Пшеницею засіяли ділянку розміром 300 м на 200 м, а решту поля засіяли житом. Скільки арів поля засіяно житом?
Виконайте вдома
255. Обчисліть.
1. 2000 : 100 ∙ 23 – 16;
2. (253 – 196) ∙ 28 – 73.
256. Площа прямокутника дорівнює 45 см2. Визначте довжину прямокутника, якщо відомо, що його ширина дорівнює 5 см.
257. Чим подібні вирази кожної пари? Чим вони відрізняються?
(24 + 48) : 8 (42 + 14) : 7 (30 + 35) : 5
(22 + 50) : 8 (40 + 16) : 7 (33 + 32) : 5
258. Вилучіть “зайве”.
1. 235 кг, 345 ц, 435 кг, 428 кг, 349 см;
2. 135 дм, 148 см, 560 м. 245 см2, 320 дм;
3. 145 а, 265 см2, 470 дм2, 320 м2,475 м.
259. Знайдіть значення виразів у першому стовпчику. Як, не виконуючи ділення у стовпчик, можна знайти значення виразів у другому й третьому стовпчиках?
162 : 18 162 : 9 180 : 18
184 : 23 184 : 8 207 : 23
– Подумайте, як можна записати ділене третього стовпчика по-іншому. так, щоб можна було усно знайти його значення.
260. Довжина прямокутника 54 м, а його ширина удвічі менша. Знайдіть периметр і площу прямокутника.
Віка накреслила схему й записала рівності.
54 : 2 = 27 (м);
27 ∙ 6 – 162 (м).
Відповідь: Рпр. = 162 м.
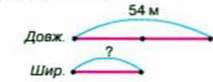
– Поясніть, як міркувала Віка. Чи згодні ви з думкою дівчинки?
261. Астрід Ліндгрен розпочала роботу над книжкою “Малюк і Карлсон, який живе на даху” в 1955 році, а закінчила повість 1968 року. Скільки років створювалась ця книжка?
262. Маса 6 однакових коробок із цукерками та 8 однакових коробок із печивом – 34 кг, а маса 9 коробок із цукерками та 4 коробок із печивом – 35 кг. Яка маса коробки з печивом?
Сергій зробив такий малюнок до задачі:

– Поясніть, як міркував Сергій.
– Запишіть дії Сергій у зошиті. Дайте відповідь на запитання.
263. Чи можна, не обчислюючи, сказати, у яких парах значення виразів будуть однакові?
84 ∙ 9 48 ∙ 9 84 + 9 49 + 8
89 ∙ 4 9 ∙ 48 9 + 84 8 + 49
264. Поясніть, як складені вирази кожного стовпчика.
26 ∙ 3 17 ∙ 5 36 ∙ 2
60 + 18 50 + 35 60 + 12
126 ∙ 3 117 ∙ 5 136 ∙ 2
300 + 78 500 + 85 200 + 72
– Міркуючи так само, складіть у зошиті свої стовпчики для поданих виразів
23 ∙ 4 21 ∙ 2 19 ∙ 3
Виконайте вдома
265. Площа актової зали – 900 м2, ширина приміщення – 25 м. Знайдіть довжину актової зали.
266. Якими можуть бути сторони квадрата, якщо його периметр 36 дм? 16 см? 12 мм?
267. Заберіть 2 палички так, щоб одержати 5 рівних квадратів.
