Вирази зі змінними. Цілі раціональні вирази
Урок № 13
Тема. Вирази зі змінними. Цілі раціональні вирази
Мета: систематизувати та узагальнити знання та вміння учнів, поглибити знання учнів.
Тип уроку: поглиблення, систематизація та узагальнення знань та вмінь.
Хід уроку
І. Перевірка домашнього завдання
До вправ № 1-2 можна записати за дошкою правильні розв’язання і звірити тільки відповіді (у ході само – або взаємоперевірки) чи зібрати зошити в учнів вибірково або фронтально. № 3 є підготовчим до сприйняття матеріалу про вирази зі змінними, що не мають змісту,
Розв’язання вправ № 1-3 домашнього завдання
№ 1. 1) 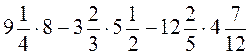 = (72 + 2) –
= (72 + 2) –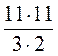 –
– 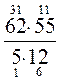 = 74 –
= 74 – 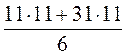 = 74 –
= 74 – 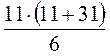 = 74 –
= 74 – 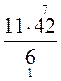 = 74 – 77 = – 3;
= 74 – 77 = – 3;
2) (-1,2 + 4,32 : (-1,8)) : (-0,001) – (-0,3) = – 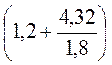 – 1000 – 0,3 = -3,6 – 1000 – 0,3 = -36 – 10 – 3 = -1080.
– 1000 – 0,3 = -3,6 – 1000 – 0,3 = -36 – 10 – 3 = -1080.
№2. 1) -16 : (-0,8 – (-0,05)) = 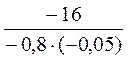 =
= 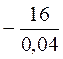 = – 400;
= – 400;
2) (1,2 + 0,8)(1,2 – 0,8) = 20,4 = 0,8;
3) (-72) – 82 = 49 – 64 = – 15;
4) 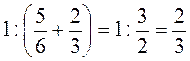 ;
;
5) -(2,86 + (-4,3)) = 4,30 – 2,86 = 1,44.
№ 3.
1) 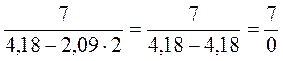 не має змісту, бо ділення числа на нуль не визначено.
не має змісту, бо ділення числа на нуль не визначено.
2) 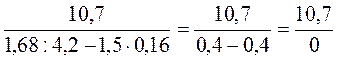 не має змісту, бо ділення числа на нуль неможливе.
не має змісту, бо ділення числа на нуль неможливе.
II. Актуалізація опорних знань
Математичний диктант
1. Закінчіть речення: “Запис, що складається з чисел, знаків дій та дужок, називають…”.
2. Чи є число 16 значенням виразу 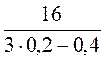 ? Чому?
? Чому?
3. Чи має зміст вираз 42 : (0,3 – 0,1 – 3)? Чому?
4. Запишіть вираз, використовуючи числа і знаки дій, та обчисліть його значення: 1) сума чисел 1,6 та 3,4; 2) різниця чисел 5 та 6,5; 3) добуток чисел 4 та 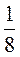 ; 4) частка числа 6 та числа, протилежного числу
; 4) частка числа 6 та числа, протилежного числу 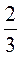 ; 5) подвоєний добуток чисел 2,3 та 1,7 на їх суму.
; 5) подвоєний добуток чисел 2,3 та 1,7 на їх суму.
@ Під час перевірки виконання завдань математичною диктанту повторюємо й узагальнюємо основні поняття попереднього уроку, а саме:
– числовий вираз;
– значення числового виразу;
– числовий вираз, що не має змісту.
III. Робота із випереджальним домашнім завданням
Задача 1. Довжина прямокутної ділянки 42 м, а ширина на 10 м менша. Запишіть вираз для знаходження площі ділянки | Задача 2. Довжина прямокутної ділянки 42 м, а ширина на b м менша. Запишіть вираз для знаходження площі ділянки |
Запитання для порівняння
1) Чим відрізняються умови задач? (У задачі 2 ширина на b м менша; b має невідоме значення; у задачі 1 ширина на 10 м менша від довжини.)
2) Чим схожі умови задач? (В обох задачах йдеться про прямокутник із довжиною 42 м; в обох задачах необхідно записати вираз, що показує, як знайти площу цього прямокутника, тому вид шуканих виразів буде однаковий: ab, де а – довжина, b – ширина.
Висновок. Вирази для розв’язання задач № 1 та 2 відрізняються тільки одним:
Задача 1. 42 – (42 – 10) – числовий вираз. | Задача 2. 42 – (42 – b) – вираз, що не є числовим, бо, крім чисел, дужок га знаків дій, містить букву b. |
Отже, все, що було відоме про числові вирази, і все, що стосується понять, пов’язаних із числовими виразами, можна поширити й на вирази, що містять замість числа (чисел) букву (букви). Єдине, що відрізняє ці два види виразів – для будь-якого числового виразу значення числового виразу (якщо воно існує) задано однозначно; для виразів, що містять букву (букви) значення може змінюватись залежно від значення букви.
IV. Поглиблення, систематизація та узагальнення знань
@ З поняттями “змінна”, “вираз зі змінними”, “значення виразу зі змінними” учні зустрічалися в молодших класах, але, на відміну від попередніх класів, вказана термінологія уводиться в 7 класі вперше. На цьому етапі також доречною буде робота з формування вмінь читати вирази із використанням термінів “сума”, “різниця” і т. д.
Розглядаючи вирази зі змінними, показуємо, що існують такі вирази, які мають зміст не при всіх значеннях змінних.
Але якщо порівняння задач 1 та 2 у випереджальному домашньому завданні проведено досконало, учні самі проводять певні аналогії і встановлюють відповідність:
Числові вирази | Вирази зі змінними |
1. Складаються з чисел, дужок, знаків дій. 2. Можуть мати значення – число, що отримують під час виконання дій. 3. Можуть не мати змісту, тобто не всі дії, записані у виразі, можна виконати | 1. Складаються з чисел, змінних, дужок і знаків дій. 2. Можуть мати числове значення, що відповідає певному значенню змінної, тобто число, яке утворився, якщо замість букви поставити її значений і знайти значення утвореною числовою виразу. 3. Можуть не мати змісту при деяких значеннях змінної, якщо в paзі підстановки цього значення у вираз утвориться числовий вираз, що не мас змісту |
Після виконаної роботи можна зробити короткі записи в зошитах учнів. Ці записи можуть мати вигляд конспекту 4:
Конспект 4 Вирази зі змінними 1. Буквений вираз (вираз зі змінними) утворюють із букв (змінних), чисел, записів дій і дужок. |
Приклад: 42 – (42 – b); abc + 2 – вирази зі змінними. |
Зауваження. Буквеним виразом (виразом зі змінними) вважають і окремо взяту букву (змінну). |
Приклад: a, b – вирази зі змінними. |
2. Значенням виразу зі змінними для даних значень змінних називають значення числовою виразу, що утворюється під час підстановки замість букв їх значень. |
Зауваження. Існують вирази зі змінними, які не мають змісту при деяких значеннях змінних. |
Приклад: |
3. Вирази, що не мають ділення на змінну, називають цілими, а вирази, що мають ділення на змінну,- дробовими. |
Приклад а + b – цілий вираз; A : b – дробовий вираз;
|
V. Засвоєння вмінь
@ Якщо із завданнями типу:
1) “знайти значення виразу зі змінними при певних значеннях букв”,
2) “прочитати і записати буквений вираз за певними умовами”
Учні працювали ще в молодших класах, то із завданням на знаходження значень змінної, при яких вираз не має змісту, учні зустрічаються вперше, і тому саме цим завданням слід приділити якомога більше уваги.
Виконання усних вправ
1. Відомо, що а і b – сторони прямокутника (у сантиметрах). Який зміст має вираз: 1) ab; 2) 2(a + b); 3)* a + b?
2. Відшукайте значення виразу х – у, якщо:
1) x = 1; y = -5; 2) x = 0; y = -2; 3) x= -1,5; y =0.
3. Прочитайте вираз, використовуючи терміни “сума”, “різниця”, “квадрат”, “кут” тощо.
1) а + с; 2) ас; 3) (а + с)2; 4) (а – с)3; 5) (а – с)(а + с).
Виконання письмових вправ
1. Заповніть таблицю, обчисливши значення виразу -2л:+3 для заданих значень х:
Х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
-2х + 3 |
2. Майстер щогодини виготовляє а деталей, а його учень – на 7 деталей менше. Скільки деталей разом виготовили майстер та учень, якщо майстер працював 6 год., а учень – 4 год.?
3. Запишіть у вигляді виразу:
1) різницю чисел 2х і 5у;
2) квадрат суми чисел а і 0,6с;
3) суму куба числа х і квадрата числа у;
4) квадрат різниці чисел т і n;
5) різницю квадратів чисел т і п;
6) півсуму добутку чисел 0,7 і с і числа -0,6.
4. При яких значеннях змінної має зміст вираз:
1) 3х + 4; 2) 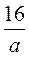 ; 3)
; 3) 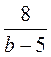 ; 4)
; 4) 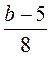 ?
?
VI. Підсумок уроку
Утворіть із виразів якомога більше груп за ознаками схожості (назвіть ці ознаки):
3; 3 + 2; 3 + а; 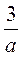 ;
; 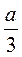 ;
; 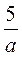 ; а.
; а.
(Повторюємо поняття: числові вирази; буквені вирази; вирази, що не мають змісту; цілі вирази; дробові вирази.)
VII. Домашнє завдання
№ 1. Знайдіть значення виразу:
1) 12 – 8х, якщо х = 4; -2; 0; 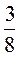 ; 2) а2 – 3а, якщо а = 5; -6; 0,1.
; 2) а2 – 3а, якщо а = 5; -6; 0,1.
№ 2. Микола купив т олівців по 50 к і 6 зошитів по п копійок. На скільки більше сплатив хлопчик за зошити, ніж за олівці? Обчисліть значення утвореного виразу при т = 2, п = 30.
№ 3. При яких значеннях змінної не має змісту вираз:
1) 2х – 5; 2) 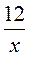 ; 3)
; 3) 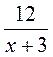 ; 4)
; 4) 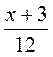 ?
?
При яких значеннях змінної вираз буде мати зміст?
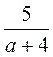 ;
;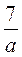 ; а : b і т. д. – вирази зі змінними, що мають ділення на змінну, а отже, не будуть мати змісту при таких значеннях змінної, коли дільник (знаменник) дорівнює 0.
; а : b і т. д. – вирази зі змінними, що мають ділення на змінну, а отже, не будуть мати змісту при таких значеннях змінної, коли дільник (знаменник) дорівнює 0.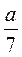 – цілий вираз;
– цілий вираз;