Головна ⇒ 📌ГДЗ з математики ⇒ Вправи 325-374

Вправи 325-374

325.

Вправи 325 374

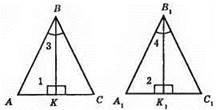
?ABC; AB = AC; ?A1B1C1; A1B1 = A1C1; ∠B = ∠B1; BK = B1K1. ∠AKB = ∠CKB = ∠A1K1B1 = ∠C1K1B1 = 90°. ?АВK = ?A1B1K1.

1) BK = В1K1; 2) ∠1 = ∠2; 3) ∠3 = ∠4, отже, AB =A1B1.

?АВС = ?А1В1С1. AB = A1B1; BC = В1С1; ∠B = ∠B1.

326.

Вправи 325 374

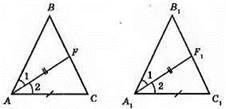
AC = A1C1; ∠A = ∠A1; AF = A1F1.

1) ?ACF = ?A1C1F1; AF = A1F1; AC = A1C1; ∠FAC = ∠F1A1C1. З рівності трикутників маємо: ∠C = ∠C1.

2) ?ABC = ?A1B1C1 за другою ознакою рівності трикутників. АС = A1C1; ∠A = ∠A1, ∠C = ∠C1.

327.

Вправи 325 374

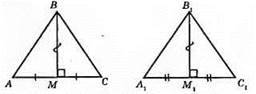
AC = A1C1; AM = MC; A1M1 = M1C1; ∠BMC = ∠B1M1C1.

?BMC = ?B1M1C1 за першою ознакою рівності, MB = MjBj, MC = M1C1, ∠M =

∠M1. Отже, ∠C = ∠C1, BC = B1C1.

?АВС = ?A1B1C1; AC = A1C1, BC = В1С1, ∠C = ∠C1 за першою ознакою рівності трикутників.

328.

Вправи 325 374

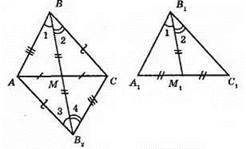
ВМ = В1М1; ∠ABM = ∠A1B1M1; ∠MBC = ∠M1B1C1.

Продовжимо медіану ВМ, відкладемо В2М = ВМ. ?АВМ = ?СВ2М, ?АМВ2 = ?CMВ за двома сторонами і кутом між ними. З рівності трикутників маємо: ∠2 = ∠3, ∠1 = ∠4. ВС = АВ2, AB = В2С. ?АВС = ?АВ2С = ?A1B1C1.

329.

Вправи 325 374

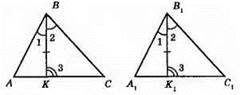
Дано: ZB = ZB1, BK = В1K1, ∠BKC = ∠В1К1C1.

?BKC = ?B1K1C1; BK = B1K1, ∠KBC = ∠K1BjC1, ∠BKC = ∠B1K1C1. З цього маємо: BC = B1C1, ∠C = ∠C1.

?ABC = ?A1B1C1 (за стороною і двома кутами). ВС = B1C1, ∠C = ∠C1, ∠B = ∠B1.

330.

Вправи 325 374

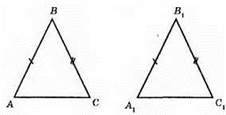
1) AB = A1B1, BC =

B1C1, ∠B = ∠B1 за першою ознакою.

2) AB = A1B1; ∠A = ∠A1, ∠B = ∠B1 за другою ознакою.

331.

Вправи 325 374

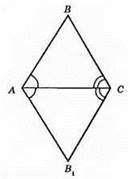
∠BAC = ∠B1AC; АС – спільна основа; ∠BCA = ∠B1CA або ∠BAC = ∠B1AC; AB = AB1; АС – спільна сторона.

332. ?ABC = ?A1B1C1, АС = А1С1, BC = B1C1, BC = B1C1.

333. Кути рівні, тому що трикутники рівні.

334. Правильно.

335. Не завжди правильно.

336.

Вправи 325 374

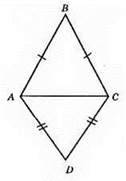
?АВС, AB = ВС; ?ADC, DС = DА.

1) ?ABD = ?CBD за третьою ознакою, AB = BC, AD = DC, BD – спільна сторона.

337.

Вправи 325 374

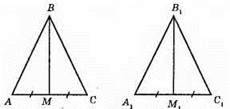
?АВМ = ?A1B1M1; ?ВМС = ?B1M1C1.

338.

Вправи 325 374

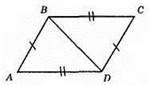
AB = CD; BC = AD; BD-спільна сторона.

?ABD = ?CDB за третьою ознакою рівності трикутників.

339.

Вправи 325 374

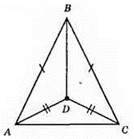
AB = CB; AD = CD; BD – спільна сторона.

?ABD = ?CDB за третьою ознакою рівності трикутників.

340.

Вправи 325 374

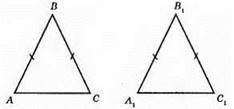
?ABC – рівнобедрений; AC = BC. ?A1B1C1 – рівнобедрений, А1С1 = B1С1.

1) АС = А1С1; 2) AB = A1B1; 3) BC = B1C1.

?ABC = ?A1B1C1 за третьою ознакою рівності трикутників.

341. 1) АB = А1В1; 2) ВС = B1С1; 3) P? ABC = P? A1B1C1;

P? ABC = AB + BC + AC;

P? A1B1C1 = А1В1 + B1C1 + А1С1; AB = A1B1; ВС = B1C1, отже, і АС = А1С1. ?АBС = ?A1B1C1 за третьою ознакою рівності трикутників.

Вправи 325 374

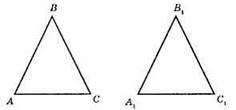
342.

Вправи 325 374

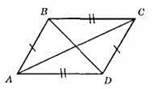
?АBС = ?CDA. З їх рівності маємо: AB = CD; BС = AD; АС – спільна сторона. Доведемо, що? ABD = ?CDB. 1) AB = CD; 2) BС = AD; 3) BD – спільна сторона.

?ABD = ?СDB за третьою ознакою рівності трикутників.

343.

Вправи 325 374

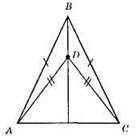
?ABC – рівнобедрений, AB = ВС; ?ADC – рівнобедрений, AD = DC.

?ADB = ?CDB; 1) AB = CB; 2) AD = CD;

3) DB – спільна сторона.

Трикутника рівні за третьою ознакою рівності трикутників. З їх рівності маємо: ∠ADB = ∠CDB.

344.

Вправи 325 374

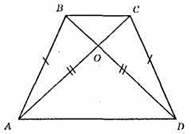
AB = CD; АС = BD; ?ABD = ?DCA за третьою ознакою рівності трикутників.

1) АB = DC; 2) BD = AC; 3) AD – спільна основа.

345.

Вправи 325 374

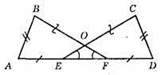
AB = CD; BF = СЕ; AE = BD; ?АВF = ?СDE; 1) AB = CD; 2) BF = СЕ; 3) АF = DЕ. З рівності трикутників маємо: ∠CEF = ∠BFE.

?EOF – рівнобедрений, бо ∠OEF = ∠OFE.

346.

Вправи 325 374

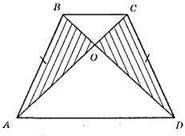
?АОВ = ?DOC; з рівності трикутників: AB = CD, AO = OD, BO = OC. ?ABC = ?DCB;

1) AB = CD;

2) ВС – спільна сторона; АС = АО + ОС;

3) BD = BO + OD ⇒ AC = BD.

?ABC = ?DCВ за трьома сторонами.

347.

Вправи 325 374

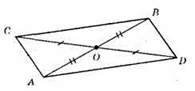
ОС = OD; AO = ВО; ?АОС = ?BOD. З їх рівності: АС = BD. ?ВОС = ?AOD. З їх рівності: ВС =AD.

?АОС = ?BOD; ?ВОС = ?AOD за першою ознакою рівності трикутників.

?ABC = ?BAD (за третьою ознакою рівності). 1) ВС = DA; АС = BD; AB – спільна сторона.

348.

Вправи 325 374

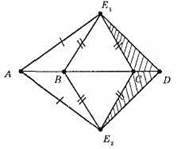
AE1 = AE2; BE1 = BE2.

Довести, що? СDE1 = ?CDE2.

1) ?АE1С = ?АЕ2С (за третьою ознакою рівності трикутників). AE1 = АЕ2; E1C = Е2С; АС – спільна сторона. З їх рівності: ∠E1CB = ∠E2CB.

?СE1D = ?CE2D за двома сторонами і кутом між ними: 1) E1С = Е2С; 2) CD – спільна сторона; ∠E1CD = ∠E2CD – кути суміжні рівним кутам.

350.

Вправи 325 374

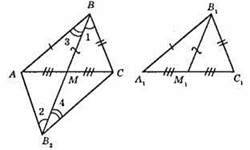
AB = А1В1; ВС = В1С1; ВМ = В1М1. Продовжимо ВМ = В2М. ?МВС = ?MB2A за трьома сторонами. З рівності трикутників маємо: ∠1 = ∠2. Аналогічно ∠3 = ∠4. ∠B = ∠B2; ?ABC = ?AB2C за двома сторонами і кутом між ними. ?ABC = ?А1В1С1.

351.

Вправи 325 374

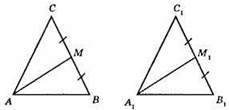
?ABC, АС = ВС, AM = AM1. ?А1В1С1, AC1 = B1C1.

?ACM = ?A1C1M1; AC = A1C1; CM = C1M1; AM = A1M1.

Трикутники рівні за третьою ознакою рівності трикутників. З рівності трикутників маємо: ∠C = ∠C1;

?ABC = ?А1В1С1 за першою ознакою рівності трикутників: АС = А1С1, ВС = В1С1, ∠C = ∠C1.

Задачі до підготовки контрольної роботи № 2

1. Периметр рівнобедреного трикутника 105 см, а бічні сторони АС : АВ = 7 : 3.

Вправи 325 374

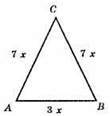
Нехай х – спільна міра відрізків, тоді AB = 3х см, АС = ВС = 7х см.

Рівняння: 3х + 7x + 7x = 105; 17х = 105;

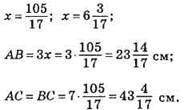
Вправи 325 374

2.

Вправи 325 374

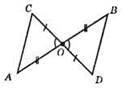
AO = DO; CO = BO; ?АОС = ?DOB за першою ознакою рівності трикутників.

1) CO = BO; 2) AO = ВО; 3) ∠COA = ∠BOD (вертикальні кути).

2) АС = 4 см, СВ = 8 см. Р? ABC = АС + АО + ОС = АС + ОС + OD = АС + CD = 4 + 8 = 12 (см).

Відповідь: 12 см.

3.

Вправи 325 374

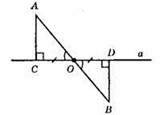
CO = DO, АС ⊥ а, ВD ⊥ а. ?АСО = ?ВDО за другою ознакою рівності трикутників. CO = OD, ∠AOC = ∠DOB, ∠ACO = ∠BDO. З рівності трикутників: АС = ВD.

4.

Вправи 325 374

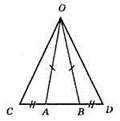
1) ?АОВ – рівнобедрений; ОА = OB, АС = BD, ∠OAB = ∠OBA.

2) ?АОС = ?BOD (за першою ознакою рівності трикутників), АС = BD, АО = BO, ∠CAO = ∠DBO (рівні кути рівним суміжним кутам).

5.

Вправи 325 374

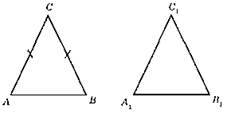
?ABC – рівнобедрений, АС = ВС; ?A1B1C1 – рівнобедрений, А1С1 = В1C1; AB = A1B1 за умовою;

P? ABC = (АС + ВС) + AB ⇒ АС + ВС = Р? ABC – АВ;

Вправи 325 374

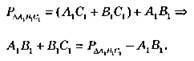
Праві частини рівностей рівні, отже

АС + ВС = A1C1 + В1С1; АС = ВС; А1С1 = B1C1; 2АС = 2A1C1; AC = A1C1; BC = B1C1.

?ABC = ?A1B1C1 за третьою ознакою рівності трикутників.

6.

Вправи 325 374

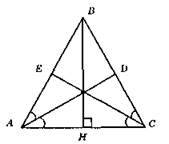
?АВС; ВН ⊥ АС; АН = НС.

?АВН = ?СВН (за першою ознакою), AH = CH, ВН – спільна сторона; ∠AHB = ∠CHB = 90°, отже, AB = ВС.

?АВС – рівнобедрений, ВН – бісектриса; AB, СЕ – бісектриси; ∠A = ∠C.

?ADC = ?СЕА, АС – спільна сторона ∠A = ∠C, ∠DAC = ∠ECA.

?АDС = ?СЕА за другою ознакою рівності трикутників, отже, AB = СЕ = 15 см.

352. а) Ні; б) так; в) ні; г) так.

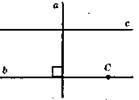
353. 1) b || c;

Вправи 325 374

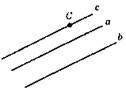
2) b || c;

Вправи 325 374

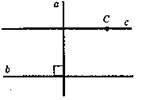
3) b || c;

Вправи 325 374

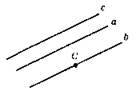
4) b || c;

Вправи 325 374

354.

Вправи 325 374

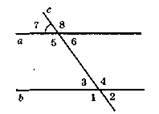
А) Внутрішні різносторонні кути: ∠4 i ∠5.

Б) Внутрішні односторонні кути: ∠4 і ∠6.

В) Відповідні кути: ∠4 і ∠8.

355.

Вправи 325 374

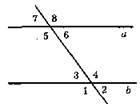
Чи буде а || b, якщо:

A) ∠3 = ∠6, так; б) ∠5 = ∠8, так; в) ∠1 = ∠7, ні; г) ∠2 = ∠6, так; д) ∠3 + ∠5 = 180°, так; е) ∠2 + ∠4 = 180°, так.

356. a) ∠6 = ∠3, то a || b; б) ∠6 + ∠4 = 180°, то a || b.

357. а) Правильне твердження; б) ні; в) ні.

358. a)

Вправи 325 374

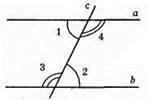
A || b, с – січна; б) ∠1 i ∠2; ∠3 i ∠4 – внутрішні різносторонні кути.

Б)

Вправи 325 374

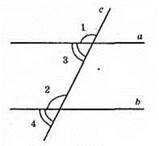
∠1 і ∠2, ∠3 і ∠4 – відповідні кути.

359.

Вправи 325 374

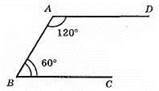
AD || ВС, тому що ∠ABC + ∠DAB = 60 + 120° = 180°.

360.

Вправи 325 374

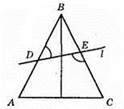
AB і ВС – прямі; DE – січна; ∠BDE і ∠CED; ∠BED і ∠ADE – внутрішні різносторонні кути. ∠BDE і ∠BED, ∠ADE і ∠CED – внутрішні односторонні.

361. а)

Вправи 325 374

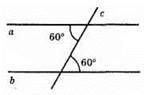
Внутрішні різносторонні кути рівні, a || b.

Б)

Вправи 325 374

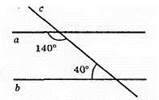
Сума внутрішніх односторонніх кутів 180°, a || b.

В)

Вправи 325 374

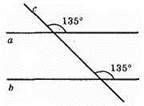
Відповідні кути рівні, a || b.

362.

Вправи 325 374

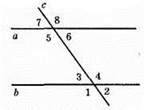
А) ∠4 = ∠5 = 125°, a || b; внутрішні різносторонні кути рівні.

Б) ∠5 = 115°, ∠3 = 65°, а || b; 115° + 65° = 180°. ∠5 і ∠3 – внутрішні односторонні кути.

В) ∠3 = 65°, ∠7 = 65°, ∠3 = ∠7 – відповідні кути, a || b.

363.

Вправи 325 374

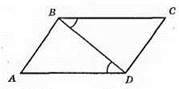
?ABD = ?CBD. З рівності трикутників ∠ADB = ∠CBD, це внутрішні різносторонні кути при прямих ВС і AD і січній BD, отже, ВС || AD.

364.

Вправи 325 374

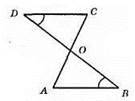
?АОВ = ?COD. З рівності трикутників маємо: ∠CDO = ∠ABO. Це внутрішні різносторонні кути при прямих DC і AB та січній DB, отже, AB || CD.

365.

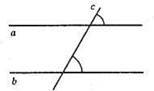
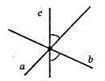
Вправи 325 374

Вправи 325 374

Ні, необов’язково.

366. a)

Вправи 325 374

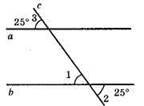
∠2 = ∠1 = 25° – вертикальні кути; ∠1 і ∠3 – відповідні кути рівні, а || b.

Б)

Вправи 325 374

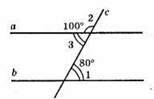
∠2 і ∠3 – суміжні кути; ∠3 = 180° – 100° = 80°; ∠3 = ∠1 – внутрішні різносторонні кути рівні, а || b.

В)

Вправи 325 374

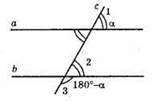
∠2 і ∠3 – суміжні кути. ∠2 = 180° – (180° – α) = 180° – 180° + α = α; ∠2 = ∠1 = α – відповідні кути, а || b.

367.

Вправи 325 374

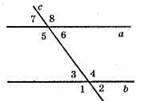
А) ∠5 = 135°; ∠4 = 3∠3;

∠3 + ∠5 = 180°; ∠3 = 180° – 135° = 45°; ∠4 = 45° x 3 = 135°;

∠5 = ∠4 = 135°, де внутрішні різносторонні кути, а || b.

Б) ∠2 = 72°; ∠6 : ∠8 = 2 : 3; ∠6 = 2х;

∠8 = 3х; ∠6 + ∠8 = 180° (суміжні кути).

2х + 3х = 180°; 5х = 180°; х = 180° : 5; х = 36°.

∠6 = 2 х 36° = 72°; ∠8 = 3 х 36° = 108°; ∠2 = ∠6 = 72°, це відповідні кути, прямі а і b – паралельні.

368.

Вправи 325 374

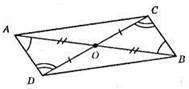
AO = OB; DO = ОС; ∠AOD = ∠COD (вертикальні кути). ?AOD = ?ВОС за першою ознакою рівності трикутників.

∠A = ∠B – внутрішні різносторонні кути при прямих AD і ВС і січній AB. Отже, AD || ВС; ∠D = ∠C – при прямих АС і BD і січній DC, отже, АС || DB.

Вправи 325 374

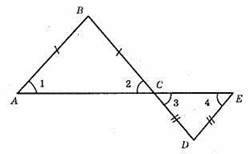
AB = ВС; CD = DE; ∠1 = ∠2; ?АВС – рівнобедрений, кути при основі рівні; ∠3 = ∠4, ?CED – рівнобедрений, кути при основі рівні; ∠2 = ∠3 (вертикальні кути).

∠1 = ∠2 = ∠3 = ∠4; ∠1 і ∠4 – внутрішні різносторонні кути при прямих AB і DE, січній AE, ∠1 = ∠4, DE || AB.

370.

Вправи 325 374

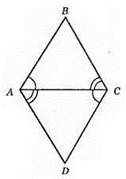
?ABC = ?CDA; ∠A = ∠C, це внутрішні різносторонні кути при прямих AD і CD та січній АС, AB || CD; ∠CAD = ∠ACB, це внутрішні різносторонні кути при прямих AD і ВС ті січній АС, отже, ВС || AD.

371.

Вправи 325 374

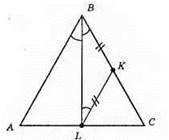
?LBK – рівнобедрений, ∠KBL = ∠KLB, ∠LBK = ∠LBA, BL – бісектриса. ∠ABL = ∠KLB – внутрішні різносторонні кути при прямих AB і KL, січна BL. Отже, AB || LK.

372.

АВ = ВС; ∠C = 80°. ?ADF – рівнобедрений, AD = DF; ∠DAF = ∠DEA.

?ABC – рівнобедрений, ∠A = ∠C; ∠DAE = 80° – 40°; ∠DEA = ∠DAE = 40°; ∠DEA і ∠DAE – внутрішні різносторонні кути при прямих DE і АС, отже, DE || AC, l || AC.

373. AD = CF; ВС = DE; ∠1 = ∠2.

Вправи 325 374

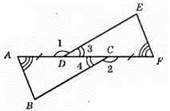
1) ∠3 = ∠4 (суміжні кути рівним кутам); 2) ВС = DE; 3) АС = DF.

?АСВ = ?FDE за двома сторонами і кутом між ними. З цієї рівності маємо: ∠CAB = ∠DFE; це внутрішні різносторонні кути при прямих AD і EF і січній AF. Отже, АВ || EF.

374.

Вправи 325 374

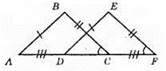
?АВС = ?DEF. 1) AB = DE; 2) ВС = EF; 3) AC = DF.

АС = AD + DC; DF = CF + DC, але AD = CF; ?ABC = ?DEF за трьома рівними сторонами. З цієї рівності маємо: ∠BCA = ∠EFD. Це відповідні кути при прямих ВС i EF i січній АВ. Отже, EF || ВС.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Вправи 225-273 225. L ⊥ AB; X – точка прямої l; О – середина AB. ?АОХ = ?BOX (за першою ознакою рівності трикутників). 1) АО = OB; 2) ∠3 = ∠4 = 90°; 3) ОХ – спільна сторона. З цього випливає АХ = ВХ, отже, точка X рівновіддалена від кінців відрізка А і В. 226. Три прямі […]...

  2. Вправи 176-224 176. Якщо три точки лежать на прямій, вони не можуть бути вершинами трикутника. 177. А) Кути прилеглі до сторони МР: ∠KMP і ∠KPM; Б) ∠KMP – протилежний стороні KP; В) сторона протилежна куту K – МР; В) сторони прилеглі до кута Р – KP і РМ. 178. Якщо два трикутники рівні, то їх периметри рівні. […]...

  3. Ознаки паралельності двох прямих § 3. Паралельні прямі. Сума кутів трикутника 13. Ознаки паралельності двох прямих Практичні завдання 300. 1) Кути АОМ і CEO – відповідні; 2) кути АОЕ і СЕК – відповідні; 3) кути АОE і OED – різносторонні; 4) кути АОЕ і CEO – односторонні. 1) відповідні; 2) односторонні; 3) різносторонні. 301. 1) ∠1 i ∠5; ∠2 […]...

  4. Вправи 275-324 275. Кут В. а) ВА = ВС, ?АВС – рівнобедрений, у нього дві сторони рівні; Б) ∠A = ∠C. 276. ∠A = 60°; AD – бісектриса кута А. BC ⊥ AD; AB = AC; ∠B = ∠C. 277. AB = ВС; АС – основа. Нехай АВ = ВС = х м, тоді АС = (х […]...

  5. Властивості й ознака рівнобедреного трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 12. Властивості й ознака рівнобедреного трикутника 476. На мал. 72: ML і МК – бічні сторони, KL – основа, ∠K = ∠L. 477. KD = DF, КЕ = EF, ∠K = ∠F, ∠KDE = ∠FDE, ∠DEK = ∠DEF = 90°. 478. Щоб провести бісектрису, медіану і […]...

  6. Рівність геометричних фігур Розділ 1. Найпростіші геометричні фігури та їх властивості § 11. Рівність геометричних фігур 397. Щоб сумістити фігури F1 i F, можна скопіювати фігуру F1 на кальку, потім перевернути кальку і покласти на фігуру F. 398. Відрізки OP і MN сумістити не можна, бо вони мають різну довжину. 399. Кути ABC і MON сумістити не можна, […]...

  7. Вправи 425-474 425. АС – основа; AB = CB; ∠ADC = 150°. ∠CAD = ∠BAD = x; ∠ACD = 2x; x + 2x + 150° = 180°; 3x = 180° – 150°; 3x = 30°; x = 10°; ∠C = ∠A = 20°; ∠B = 180° – (20° + 20°) = 140°. Відповідь: 20°, 20°, 140°. 426. […]...

  8. Вправи 475-524 475. ?ABC – прямокутний; ∠A = 30°; АС = 18 см; ВК – бісектриса, проведена до катета АС; ∠CBK = ∠ABK = ∠CBA : 2 = 60° : 2 = 30°; ∠CBA = 90° – ∠CAB = 90° – 30° = 60°; СК = х, тоді AK = 18 – х. ?АВК – прямокутний; ∠A […]...

  9. Вправи 375-424 375. ВС – бісектриса ∠ABD; ∠ABD = 80° + 80° = 160°; ∠BAC + ∠ABD = 20° + 160° = 180°; ∠BAC і ∠ABD – внутрішні односторонні кути при прямих АС і BD та січній АВ. Отже, BD || АС. 376. ∠A = 70°, ∠B = 40°, BE – бісектриса ∠ABD; ∠DBE = ∠ABE = […]...

  10. Перша та друга ознаки рівності трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 13. Перша та друга ознаки рівності трикутників 301. На рис. 227 трикутники рівні за першою ознакою (за двома сторонами і кутом між ними). На рис. 228 трикутники рівні за другою ознакою (за стороною і прилеглими двома кутами). 302. У? ABC і? CDA спільний елемент – сторона AВ. У? […]...

  11. Властивості прямокутного трикутника § 3. Паралельні прямі. Сума кутів трикутника § 17. Властивості прямокутного трикутника 457. Найбільший катет трикутника дорівнює 24 см. 458. ?DEF – прямокутний, ∠F = 90°, ∠D = 30°, DE = 18 см. Відповідь: 9 см. 459. ?KCM – прямокутний, ∠M = 90°, ∠C = 60°, MC = 7 см. ∠MKC = 90° – 60° […]...

  12. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника Розділ 3. Трикутники. Ознаки рівності трикутників § 15. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника 351. 1) AT – висота трикутника ABC. 2) AN – медіана трикутника ABC. 3) АР – бісектриса трикутника? AВС. 352. Оскільки AK – висота, то ∠BKA = ∠CKA = 90°. 353. Оскільки АК – бісектриса, то ∠BAK = […]...

  13. Вправи 525-574 525. АВ = CD; AO : OB = CO : OD; ?СОВ = ?AOD (за двома сторонами і кутом МІНІ ними). З рівності трикутників маємо: BC = AD. ?ВСА = ?DAC. 1) АС – спільна сторона; 2) AB = CD; 3) BC = DA; ∠MCA = ∠MAC; отже, ∠A = ∠C; ?CMА – рівнобедрений; МС […]...

  14. Рівнобедрений трикутник і його властивості § 2. Трикутники 8. Рівнобедрений трикутник і його властивості Практичні завдання 196. 197. 198. Вправи 199. 1) Р = 13 + 2 х 8 = 29(см). Відповідь: 29 см. 2) Нехай х см – бічна сторона, тоді 15 + 2х = 39, тоді 2х = 39 – 15; 2х = 24; х = 24 : […]...

  15. Ознаки рівнобедреного трикутника § 2. Трикутники 9. Ознаки рівнобедреного трикутника 232. ?ABC – рівнобедрений, тому ВК є бісектрисою кута ABC, отже, ∠ABC = 2 х ∠ABK = 2 x 25° = 50°. Відповідь: 50°. 233. BK є висотою та медіаною, тому? ABC – рівнобедрений, AB = ВС, отже, ∠C = ∠A =17°. Відповідь: 17°. 234. AС = ВС, […]...

  16. Вправи для повторення до розділу 2 Розділ 2. Взаємне розміщення прямих па площині Вправи для повторення до розділу 2 До § 5. 226. На рис. 184 суміжні кути ∠2 і ∠3. на рис. 185 суміжні кути ∠1 і ∠4 та ∠2 i ∠3. На рис. 186 суміжні кути ∠1 і ∠2 та ∠3 i ∠4. 227. 1) Так, можна. Треба побудувати […]...

  17. Коло і круг Розділ 1. Найпростіші геометричні фігури та їх властивості § 15. Коло і круг 588. 1) Хордами є відрізки: KB, NC, KN, CB, LD. 2) Діаметрами є відрізки: LD, NC, КВ. 3) Радіусами кола є відрізки: OL, OK, ОС, OD, OB, ON. 589. Дотичні до кола: АС, CB, AB. ON ⊥ AC, ОМ ⊥ CB, OK […]...

  18. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих Розділ 2. Взаємне розміщення прямих па площині § 9. Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих 170. Рис. 119: ∠1 і ∠2 – внутрішні різносторонні кути. Рис. 120: ∠1 і ∠2 – відповідні кути. Рис,121: ∠1 i ∠2 – внутрішні різносторонні кути. 171. Внутрішні односторонні кути: ∠ANM і ∠NMB, ∠CNM і ∠NMD. […]...

  19. Вправи 625-682 625. Геометричним місцем центрів кіл радіуса R, що проходить через дану точку А, є коло із центром в точці А і радіусом R. 626. Геометричним місцем центрів кіл, що дотикаються до сторін даного нерозгорнутого кута, є бісектриса даного кута без його вершини О. ОК – бісектриса. 627. Геометричним місцем точок С, які є вершинами трикутників […]...

  20. Ознаки рівності прямокутних трикутників Розділ 1. Найпростіші геометричні фігури та їх властивості § 14. Ознаки рівності прямокутних трикутників 549. Ні, трикутники не рівні. 550. Мал. 319. ?САВ = ?HDQ (за катетом і гострим кутом: CA = HD, ∠C = ∠H). Мал. 320. ?ABC = ?CDA (за гіпотенузою АС і гострим кутом: ∠BAC = ∠DAC). Мал. 321. ?АОВ = ?DCО […]...

  21. Вправи 100-49 100. А || b, с || d. 4 точки перетину. 101. 1) Всі чотири прямі перетинають пряму с. 2) Одна пряма паралельна, три перетинають пряму с. 102. 1) m || с; 2) m || b; в) m || а. 103. а || b. Якщо b i c не перетинаються, то через т. М проведено 2 […]...

  22. Описане та вписане коло трикутника § 3. Паралельні прямі. Сума кутів трикутника § 20. Описане та вписане коло трикутника 540. 1) Різносторонній гострокутний трикутник. 2) Прямокутний трикутник. 3) Тупокутний трикутник. 541. 1) Рівнобедрений гострокутний трикутник. 2) Рівнобедрений тупокутний трикутник. 542. 543. 544. Вправи 545. Медіана BD рівнобедреного трикутника ABC є в той же час і серединним перпендикуляром до сторони АС […]...

  23. Властивості кола. Дотична до кола § 3. Паралельні прямі. Сума кутів трикутника § 19. Властивості кола. Дотична до кола Практичні завдання 507. АК = КВ. 508. AB ⊥ CD – дотичні до кола. 509. АС i ВС – дотичні до кола. 510. Таких кіл може бути два. Вправи 511. CD ⊥ AB. ?АОК = ?ВОК (за катетом і гіпотенузою: ОК […]...

  24. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною Розділ 2. Взаємне розміщення прямих па площині § 10. Властивість паралельних прямих. Властивості кутів, утворених при перетині паралельних прямих січною 199. 1) ∠1 = ∠8, ∠6 = ∠3 (як відповідні кути при паралельних прямих а і b і січній с). 2) ∠2 = ∠4 (як внутрішні різносторонні кути при паралельних прямих а і b і […]...

  25. Сума кутів трикутника. Нерівність трикутника § 3. Паралельні прямі. Сума кутів трикутника § 15. Сума кутів трикутника. Нерівність трикутника Вправи 357. Нехай х° – третій кут трикутника, тоді 35 + 96 + х = 180, звідси х + 131 = 180; х = 180 – 131; х = 49. Отже, третій кут дорівнює 49°. Відповідь: 49°. 358. Нехай х° – […]...

  26. Вправи 150-175 150. ∠1 = 90°, ∠2 = ∠1 = 90° – вертикальні кути; ∠3 – суміжний куту ∠1. ∠3 = 180° – 90° = 90°, ∠3 = ∠4 = 90° (вертикальні кути). 151. ∠(ac) = 70°; ∠(ab) = 90°; ∠(bc) = 90° – ∠(ac) = 90° – 70° = 20°. 152. а ⊥ с; ∠(ab) = […]...

  27. Вправи 575-624 575. АВ і АС дотикаються до кола з центром О у точках В і С. ∠CBO = 40°. ?АBО – прямокутний, OB ⊥ AB (OB – радіус, проведений в точку дотику). ?АСО – прямокутний (ОС – радіус, проведений в точку дотику). ∠ABO = 90°; ∠ACO = 90°; ?ВОС – рівнобедрений, OB = ОС; ∠OBC = […]...

  28. Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...

  29. РІВНОБЕДРЕНИЙ ТРИКУТНИК РОЗДІЛ 3 ТРИКУТНИКИ & 13. РІВНОБЕДРЕНИЙ ТРИКУТНИК Трикутник називають рівнобедреним, якщо в нього дві сторони рівні. Рівні сторони рівнобедреного трикутника навивають бічними сторонами, а третю його сторону – основою. Трикутник, який не є рівнобедреним, називають різностороннім. Трикутник, у якого всі сторони рівні, називають рівностороннім. Рівносторонній трикутник є окремим видом рівнобедреного трикутника (мал. 166). Рівнобедрений трикутник […]...

  30. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників Розділ 3. Трикутники. Ознаки рівності трикутників § 19. Прямокутні трикутники. Властивості та ознаки рівності прямокутних трикутників 466. 1) PF – гіпотенуза, PL і LF – катети. 2) PF довша за PL, PF довша за LF, оскільки PF – гіпотенуза. 467. На рис. 321 трикутники рівні за двома катетами. Оскільки АС = ML, СВ = LP, […]...

  31. Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...

  32. Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...

  33. Взаємне розміщення двох кіл Розділ 4. Коло і круг. Геометричні побудови § 25. Взаємне розміщення двох кіл 656. На рис. 404 кола перетинаються. На рис. 405 кола дотикаються. На рис. 406 кола не мають спільних точок. 657. 1) Кола мають внутрішній дотик. 2) Кола перетинаються. 3) Кола концентричні. 658. 1) Кола мають зовнішній дотик. 2) Кола не перетинаються. 659. […]...

  34. Ознаки рівності трикутників Геометрія Основні властивості найпростіших геометричних фігур Ознаки рівності трикутників Теорема 1 (перша ознака рівності трикутників – за двома сторонами й кутом між ­ними). Якщо дві сторони й кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. Теорема 2 (друга ознака рівності трикутників – за стороною […]...

  35. Кути – ПЛАНІМЕТРІЯ Формули й таблиці МАТЕМАТИКА ПЛАНІМЕТРІЯ Паралельні прямі перетинають сторони кута. Кути Кут – плоска фігура, що складається із двох променів зі цільним початком й обмеженої ними частини площини. Промені називаються сторонами, їхня спільна точка – вершиною, обмежена ними частина площини – внутрішньою областю. α + α’ = 180° α і α’ – суміжні кути β […]...

  36. Дотична до кола, її властивості Розділ 4. Коло і круг. Геометричні побудови § 22. Дотична до кола, її властивості 607. Проведемо радіус ОР, а потім за допомогою косинця побудуємо пряму m, перпендикулярну до радіуса. За теоремою 2 пряма m є дотичною до кола. 608. Проведемо радіус ОМ, а потім за допомогою косинця побудуємо пряму n, перпендикулярну до радіуса. За теоремою […]...

  37. Вправи для повторення розділу 4 Розділ 4. Коло і круг. Геометричні побудови Вправи для повторення розділу 4 До § 21. 756. AB – діаметр, ОС – радіус. AD – хорда. 757. 1) Коло з променем ОК має одну спільну точку. 2) Коло з прямою ОК має дві спільні точки. 758. ?АОВ = ?ВОС за двома сторонами і кутом між ними […]...

  38. Паралельні прямі Геометрія Основні властивості найпростіших геометричних фігур Паралельні прямі На рисунку зображені кути, утворені в результаті перетину двох прямих січною: і ; і – внутрішні різносторонні кути при прямих a, b і січній c. і ; і – внутрішні односторонні. і ; і – зовнішні односторонні. і ; і – зовнішні різносторонні. і ; і ; […]...

  39. Коло і його елементи Розділ 4. Коло і круг. Геометричні побудови § 21. Коло і його елементи 578. PL – хорда, що проходить через центр кола, називається діаметром. 579. 1) 5 х 2 = 10(см); 2) 4,7 х 2 = 9,4 (дм). 580. 1) 8 мм х 2 = 16 мм; 2) 4,8 см х 2 = 7,6 см. […]...

  40. Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...

Ви зараз читаєте: Вправи 325-374
«
»