Вправи для повторення розділу 1
До § 1.
617. Цілі раціональні вирази:
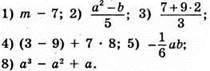
Дробові раціональні вирази:
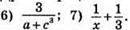
А + с
618. 50а кг завезли цукру. Якщо а = 12, то 50а = 50 • 12 = 600 (кг).
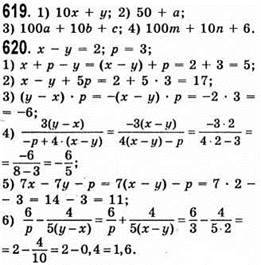
До § 2.
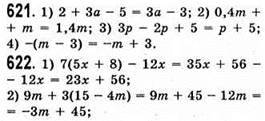
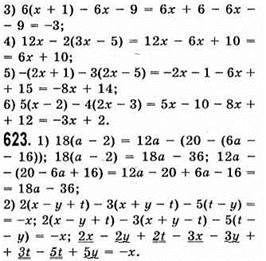
624. n, n + 1, n + 2 – три послідовні цілі числа;
N + (n + 1) + (n + 2) = 3n + 3 = 3(n + 1) ділиться на 3.
625. 1) |а + 5| = а + 5, ні; 2) |m2 + 1| = m2 + 1, так; 3) |m – n| = |n – m|, так; 4) |а| + |b| = |а + b|, ні.
До § 3.
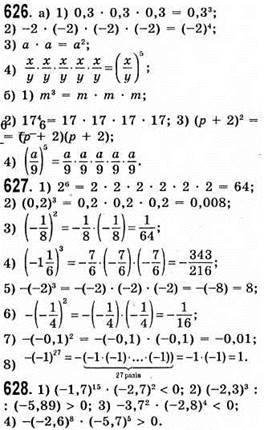
629. 1) 201513 – остання цифра 5;
2) 50117 –
3) 100617 – остання цифра 6;
4) 159 + 168 + 10117 – остання цифра (5 + 6 + 1 = 12) – 2.
630. 1) 1017 + 5 кратно числу 3, бо сума цифр 6 ділиться на 3;
2) 1029 + 7 кратним числу 9 не буде, бо сума цифр 8 не ділиться на 3.
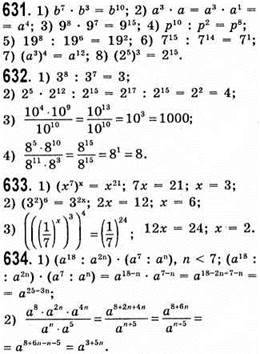
635. 1) 84n; (84)n – остання цифра 6; 2) 74n+1; 74n – 71 – остання цифра 7.
До § 5.
636. Одночлени: 1) – a2с; 2) 7а • 2b • 4; 3) 17; 4) aaba; 7) – р2.
Одночлени подано у стандартному вигляді: 1) – а2с; 3) 17; 7) – р2.
637.
Одночлен у стандартному вигляді | Коефіцієнт | Степінь | |
1) |
| -1 | 11 |
2) | 3m | -30 | 10 |
3) | -7ар2 • 0,1а2р9 = -0,7а3р11 | -0,7 | 14 |
4) |
| 1 | 5 |
5) | -а • (-b) • (-с) • (-5d) = 5abcd | 5 | 4 |
6) | Р9 • (-2а2) • (-5р7) • а8 = 10а10р16 | 10 | 26 |
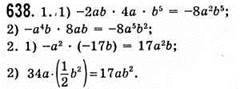
До § 6.
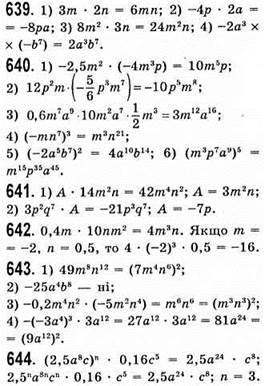
До § 7.
645. 1) 5а2 + 4b, друга степінь;
2) – а2 + аb + m, друга степінь;
3) 5с3 – 8, третя степінь;
4) 3mn2 + 4mn – 5m2n – 7, третя степінь.
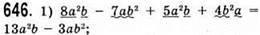
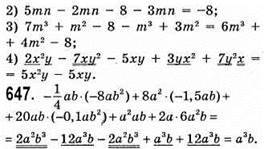
Якщо а = 5, b = -1/25, то
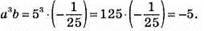
648. 2а2 + 6а + 7, натуральних значень змінної а, при яких значення многочлена є парним числом, не існує: 2а2 – парне; 6а – парне; 7 – непарне.
До § 8.
652. 2n – 1 і 2n + 1 – послідовні непарні цілі числа;
2n – 1 + 2n + 1 = 4n – ділиться на 4.
Якщо х = -1, у = 3, то 2 • (-1) • 3 + 7 • (-1) • 32 = -6 – 63 = -69.
Відповідь: -69.
До § 9.
Якщо х = -5, у = -10, то 2 • (-5)2 – (-10) = 2 • 25 + 10 = 60.
Якщо m = -3, то -(-3)2 + 2 = -9 + 2 = -7.
Відповідь: 2.
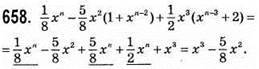
659. Нехай за другий день продали х ц овочів, а за перший день (х + 3) ц овочів, а за третій –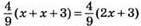 
ц було овочів продано.
Рівняння:
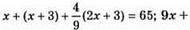
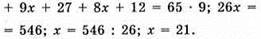
За другий день продали 21 ц, а за перший 24 ц, а за третій день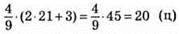 
овочів.
Відповідь: 21 ц; 24 ц; 20 ц.
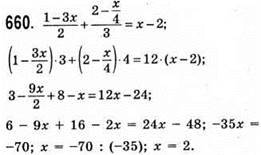
Відповідь: 2.
До § 10.
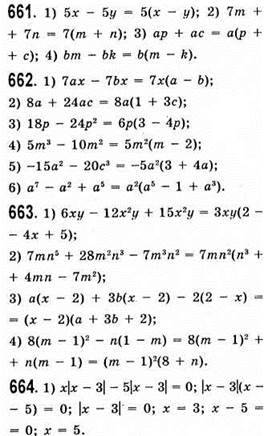
Відповідь: 3, 5.
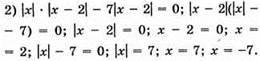
Відповідь: 2; 7; -7.
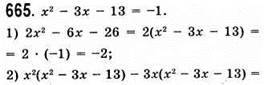
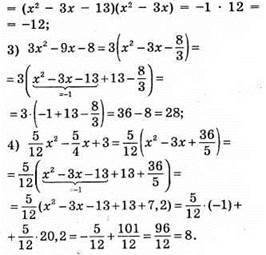
До § 11.
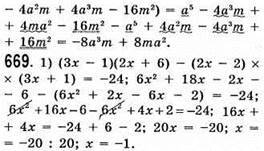
Відповідь: -1.
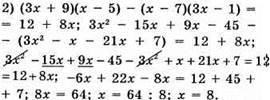
Відповідь: 8.
672. Нехай x см – ширина першого акваріуму, (x + 10) см – довжина першого акваріуму. x • (x + 10) • 25 (см3) – об’єм води у першому акваріумі.
(x + 10) см – ширина другого акваріуму; (x + 30) см – довжина другого акваріуму; (x + 30)(х + 10) • 25 (см3) – об’єм води у другому акваріумі.
37,5 л = 37,5 дм3 = 37 500 см3.
Рівняння: x(x + 10) • 25 + 37 500 = (x + 30(x + 10) • 25; 25×2 + 250x + 37 500 = (х2 + 10x + 30x + 300) • 25; 250x – 1000x = 7500 – 37 500; 750x = 30000; x = 30 000 : 750; x = 40.
Довжина: 50 см. Ширина: 40 см.
Відповідь: 40 см; 50 см.
До § 12.
Якщо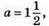 
то 
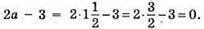
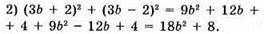
Якщо b = -1/3, то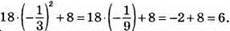 
680. x – число; x2 – квадрат числа;
(x + 3)2 = х2 + 159; х2 + 6x + 9 = х2 + 159; 6x = 150; x = 25.
Відповідь: 25.
681. (а – b)2 = |а – b|2 є тотожність.
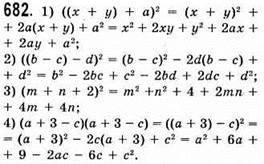
До § 14.
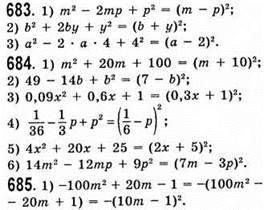
Якщо m = 0,1, то (10 • 0,1 – 1)2 = (1 – 1)2 = 0; якщо m = -0,9, то (10 • (-0,9) – 1)2 = (-10)2 = 100.
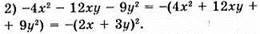
Якщо x = 0,03, у = -0,02, то -(2 • 0,03 + 3 • (-0,02)) = -(0,06 – 0,06) = 0.
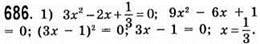
Відповідь: 1/3.
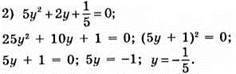
Відповідь: -1/5.
689. 1) (b – x)(b + x) = b2 + x2; b2 – x2 = b2 + x2, не є ТОТОЖНІСТЬ;
2) (с – d)(c + d) – с2 – d2 – ТОТОЖНІСТЬ;
3) (m + n)(m – n) = (m + n)2, не є ТОТОЖНІСТЬ;
4) (р – q)(p – q) = р2 – q2 – ТОТОЖНІСТЬ.
Якщо у = 1/5, то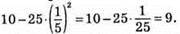 
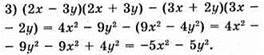
Якщо x = 1,8, у = -1,8, то -5 • 1,82 -5 • (-1,8)2 = -5 • 1,82 – 5 • 1,82 = -10 • 3,24 = -32,4.
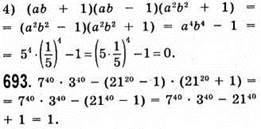
До § 16.
694. 1) m2 – р2 = (m + р)(m – р) – тотожність;
2) а2 – 72 = (а – 7)(а + 7) – тотожність;
3) с2 – d2 = (с – d)(c + d) – тотожність;
4) 92 – а2 = (9 – а)2 – не є тотожність.
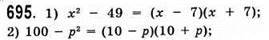
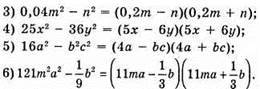
696. 1) a2x2 – b2 = 0;
(ax – b)(ax + b) = 0;
Ax – b = 0; ax = b; x = b/a;
Або ax + b = 0; ax = – b; x = – b/a.
Відповідь: b/a; – b/a.
2) x2 – 0,09a2 = 0; (x – 0,3a)(x + 0,3a) = 0; x = 0,3a; x = -0,3a.
Відповідь: 0,3a; -0,3a.
697. 1) 1382 – 1362 = (138 – 136) • (138 + 136) = 2 • 274 = 4 • 137 ділиться на 4;
2) 3492 – 3472 = (349 – 347) • (349 + 347) = 2 • 696 = 2 • 3 • 232 = 6 • 232 ділиться на 6.
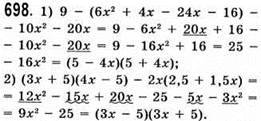
До § 17.
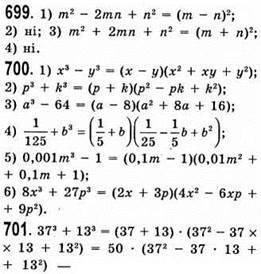
Ділиться на 50, один із множників є 50.
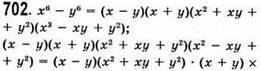
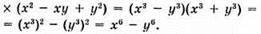
До § 18.
(1 votes, average: 5.00 out of 5)
Loading...