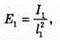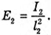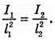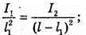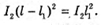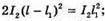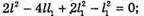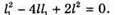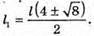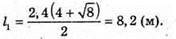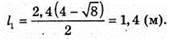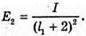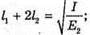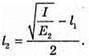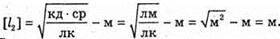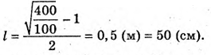ХВИЛЬОВА ТА ГЕОМЕТРИЧНА ОПТИКА
Вправа 25
1.
Дано: D1 = S1O D2= S2O Δ – ? | Розв’язання: Максимум освітленості від когерентних джерел світла спостерігається, якщо геометрична різниця ходу дорівнює цілому числу довжини хвиль: Δ = d2- d1= kλ. Оскільки S1O = S2O, το Δ = S2O – S1O = 0, k = 0. В точці О буде спостерігатися максимум освітленості для будь-яких довжин хвиль. |
2.
Дано: λ = 600 нм = 6 х 10-7 м K = 1 А = |ОС| = 4 м B = |S1S2| = 1 мм = 10 -3 м L | Розв’язання: Введемо позначення: |S1A| = d2, IS2Al = d1; |CO| = a, |S1S2| = b, |QA| = l. Максимум освітленості від когерентних джерел світла спостерігається, якщо геометрична різниця ходу дорівнює цілому числу довжин хвиль: Δ = d2- d, = kλ. Оскільки k = 1, то d2- d1 = λ.
З теореми Піфагора:
Оскільки а >> b, то d2 + d1 = 2a. 2 lb = 2 aλ; Перевіримо одиницю фізичної величини:
Знайдемо числові значення:
Відповідь: перший максимум освітленості спостерігатиметься на відстані 2,4 мм. |
3.
Дано: . L = 1,2 мм = 1,2 x 10 – 3 м A = |OC| = 2 м B = |S1S2| = 1 мм = 10-3 м λ – ? | Розв’язання:
Введемо позначення: |S, S2| = b, |OC | = a, |AB| = l, X1 = |OA|, x2 = |OB|. Максимум освітленості від когерентних джерел світла спостерігається, якщо геометрична різниця ходу дорівнює цілому числу довжин хвиль: Δ1 = k1λ1, Δ2 = k2λ2 = (k1 + 1)λ. З теореми Піфагора:
Оскільки а >> Ь, то d + d = 2α. 2xb = 2akλ; Отже,
Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: довжина хвилі світла 600 нм. |
4.
Відстань між сусідніми освітленості: А – відстань від джерел до екрана; B – відстань між джерелами світла. Де А) Збільшення відстані до екрана а призводить збільшення відстані між максимумами освітленості l. Адже, l =а. Б) Зменшення відстані між джерелами світла b призводить до збільшення відстані між максимумами освітленості l. Адже, В) Зменшення дожини хвилі λ призводить до з меншення відстані між максимумами освітленості l. Адже, l = λ. |
Вправа 26
1.
Дано: λ1 = 6,7 x 10-7 м λ2 = 4 x 10-7 м Δl1 = 3 мм = 3 х 10-3 м Δl2 – ? | Розв’язання:
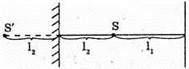
У відбитому світлі відбувається втрата півхвилі. Тоді оптична різниця ходу дорівнює: Максимум освітленості спостерігається, якщо оптична різниця ходу дорівнює цілому числу довжини хвиль: Δ = kλ1. Отже, Відстань між сусідніми червоними смугами дорівнює Δl = l1 – l2 З властивостей прямокутного трикутника:
Тоді Для синього світлофільтру: Перевіримо одиницю фізичної величини: Знайдемо числове значення:
Відповідь: відстань між синіми смугами 1,8 мм. |
2.
Дано: λ1 = 630 нм = 6,3 х 10-7 м λ2 = 450 нм = 4,5 х 10-7 м N = 1,33 D – ? | Розв’язання: У відбитому світлі відбувається втрата півхвилі. Тоді оптична різниця ходу дорівнює: Максимум освітленості спостерігається, якщо різниця ходу дорівнює цілому числу довжин хвиль: Δ1 = kλ1 Ближчий до нього мінімум спостерігається, якщо:
Отже,
Підставимо отримане значення в (1):
Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: товщина плівки 296 нм. |
3.
Дано: D = 0,5 мкм = 5 х 10-7 м λ = 590 нм = = 5,9 х 10-7 м n = 1,48
| Розв’язання: Плівка буде здаватися жовтою, якщо оптична різниця ходу дорівнює парному числу півхвиль: Плівка буде здаватися чорною, якщо оптична різниця ходу дорівнює непарному числу півхвиль: В тонкій плівці оптична різниця дорівнює: Δ = 2dn. Отже, плівка буде жовтою, якщо Плівка буде чорною, якщо Перевіримо одиницю фізичної величини: Знайдемо числове значення:
Отже, пластинка буде чорною. Якщо нахиляти плівку відносно променів, то вона буде здаватися то чорною, то жовтою. |
4.
Дано: N = 1,33 λ = 546 нм = 5,46 x 10-7 м Δl = 2 см = 2 x 10-2 μ Δk = 4 α – ? | Розв’язання:
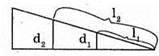
Максимум освітленості спостерігається, якщо оптична різниця ходу – дорівнює цілому числу довжин хвиль: Δ1 = k1λ, Δ2 = k2λ. В тонкому клині різниця ходу становить: Δ1 = 2d1n, Δ2= 2d2n. Отже, 2d1n = k1λ, З властивостей прямокутного трикутника:
Тоді Перевіримо одиницю фізичної величини: Знайдемо числове значення:
Відповідь: заломний кут клина 4,11 х 10-5 рад. |
5.
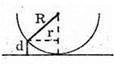
Дано: Rk = 4 мм = 4 x 10-3 м Гk+1 = 4,38 мм = = 4,38 x 10-3 м R = 6,4 м K – ? λ – ? | Розв’язання:
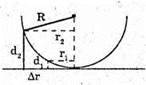
Темне кільце спостерігається, якщо Оптична різниця ходу у відбитому світлі: Оскільки між лінзою і пластинкою повітряний простір, То n = 1. З теореми Піфагора: Оскільки 2R >> dk, то Тоді Для наступного кільця: Перевіримо одиниці фізичних величин:
Знайдемо числові значення:
Відповідь: порядкові номери кілець 5 та 6; довжина хвилі 500 нм. |
6.
Дано: λ = 600 нм = 6 χ 10-7 м K = 5 D – ? | Розв’язання: Темне кільце спостерігається, якщо Оптична різниця ходу у відбитому світлі: Оскільки між лінзою і пластиною повітряний простір, то N = 1. Отже, Перевіримо одиницю фізичної величини: [d] = м. Знайдемо числове значення:
Відповідь: товщина повітряного простору 1,5 мкм. |
7.
Дано: R = 15 м K1 = 5 K2 = 25 Δг = 9 мм = 9 х 10 -3 м λ – ? | Розв’язання:
Світле кільце спостерігається, якщо Δ1 = k1λ, Δ2= k2λ. Оптична різниця ходу у відбитому світлі: Оскільки між лінзою і пластиною повітряний простір, то N = 1: З теореми Піфагора:
Оскільки 2R >> d, то Тоді оптична різниця ходу:
Звідси Відстань між кільцями:
Отже, Перевіримо одиницю фізичної величини: Знайдемо числове значення:
Відповідь: довжина хвилі 270 нм. |
8.
Дано: R1 = 1,25 r 2 N2 – ? | Розв’язання: Рис. із впр. 26.5. Темне кільце спостерігається, якщо Оптична різниця ходу у відбитому світлі:
Оскільки між лінзою і пластиною спочатку знаходилося повітря, то n1 = 1. З теореми Піфагора:
Оскільки 2R >> d, то Тоді оптична різниця ходу:
Відповідь: показник заломлення рідини 1,56. |
Вправа 27
1.
Дано: K = 1 λ = 550 нм = 5,5 х 10-7 м D = 0,02 мм = 2 х 10-5 м φ – ? | Розв’язання: Визначимо кут відхилення променів із формули дифракційної гратки: kλ = d sin φ; Перевіримо одиницю фізичної величин: Знайдемо числове значення:
φ = 1º31′. Відповідь: кут відхилення становить 1º31′. |
2.
Дано: D = 4 мкм = 4 х 10-6 м Δφ = 2º30′ K1 = 2 K1 = З λ – ? | Розв’язання:
З формули дифракційної гратки: k1λ = d sin φ1; K2λ = d sin φ2. Оскільки кути відхилення малі, то sin φ1 ≈ φ1, Sin φ2= φ2. k1λ = dφ1,
Тоді Перевіримо одиницю фізичної величини: Знайдемо числове значення. Виразимо Δφ в радіанах:
Відповідь: довжина хвилі 170 нм. |
3.
Дано: λ1 = 656 нм = 6,56 х 10-7 м λ2 = 410 нм = 4,1 х 10-7 м φ = 41º D – ? | Розв’язання: Лінії суміщаються, коли дифракційні спектри різних порядків перекривають один одного. З формули дифракційної гратки: K1λ1 = d sin φ, k2λ2 = d sin φ. Отже, k1λ1 = k2λ2. Знайдемо числові значення k1, та k2:
Отже, k1 = 5, k2 = 8. Тоді період дифракційної гратки дорівнює:
Перевіримо одиницю фізичної величини: [d] = м. Знайдемо числове значення.
Відповідь:, період дифракційної гратки 5 мкм. |
4.
Дано: φ = 20º λ1 = 669 нм = 6,69х10-7м λ2 = 446 нм = 4,46 х 10 -7 м K1max= 5 D – ? | Розв’язання: З формули дифракційної гратки: K1λ1 = d sin φ, k2λ2 = d sin φ. Отже, k1λ1 = k2λ2 Знайдемо числові значення k1та k2: Звідси k1 = 2, k2 = 3. Тоді період дифракційної гратки дорівнює: Перевіримо одиницю фізичної величини: [d] = м, Знайдемо числове значення: sin 20º = 0,342.
Відповідь: період дифракційної гратки 3,9 мкм. |
Вправа 28
1.
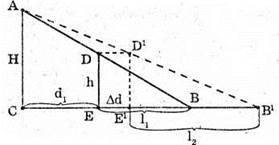
Дано: H = 0,9 м L1 = 1,2 м Δd = 1 м L2 = 1,5 м H – ? | Розв’язання:
З подібності трикутників ABC та DBE можна записати: З подібності трикутників АВ′С та D′B′E′ можна, записати:
Звідси Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: ліхтар висить на висоті 3,9 м. |
2.
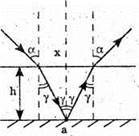
Дано: H = 1,2 м α = 30º N = 1,33 L – ? | Розв’язання:
Відстань, на якій промінь вийде з води, дорівнює: l = 2x. З властивості прямокутного трикутника: х = h tg γ. Знайдемо γ із закону Снелліуса:
Отже, γ = 22,08º, tg 22,08º = 0,406. l = 2h tg γ. Перевіримо одиницю фізичної величини: [l] = м. Знайдемо числове значення: L = 2 х 1,2 х 0,406 = 0,97 (м) = 97 (см). Відповідь: промінь вийде з води на відстані 97 см. |
3.
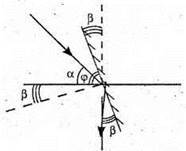
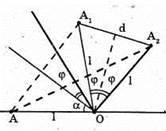
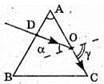
Дано: α = 38º φ – ? | Розв’язання:
З геометричної побудови видно, що φ + β = 90°, α + 2β = 90º. Оскільки Знайдемо числове значення:
Відповідь: дзеркало потрібно-поставити під кутом 64º. |
4.
Дано: α L φ D – ? | Розв’язання:
Зображення монети повернеться на кут Властивості прямокутного трикутника |
5.
Дано: R = 80 см = 0,8 м
L1 – ? | Розв’язання:
Фокусна відстань ввігнутого дзеркала: Формула увігнутого дзеркала: Лінійне збільшення Звідси Отже,
Перевіримо одиницю фізичної величини: [l1] = м. Знайдемо числове значення:
Відповідь: предмет слід розташувати на відстані 60 см від дзеркала. |
6.
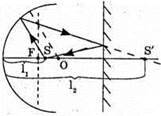
Дано: R = 40 см = 0,4 м L1 = 30 см = 0,3 м L – ? | Розв’язання:
Точку S’ можна розглядати як уявне зображення точки S в плоскому дзеркалі. Тому плоске дзеркало розташовують на середині відрізку SS’. Фокусна відстань увігнутого дзеркала Плоске дзеркало має знаходитися на відстані:
Знайдемо l2 з формули увігнутого дзеркала.
Тоді Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: дзеркало слід розташувати на відстані 45 см. |
Вправа 29
1.
Дано: L = 4 cm = 4 x 10-2 м N= 1,5 D – ? | Розв’язання:
Точка розміщена в точці А. Зображення цієї точки, яке бачить спостерігач знаходиться в точці А’. З властивості прямокутного трикутника: A = l tg α; Тоді l tg а = d tg γ; Вважаючи, що кути а та γ малі, можна записати: Із закону Снелліуеа: Отже, d = ln. Перевіримо одиницю фізичної величини: [d] = м. Знайдемо числове значення: D = 4 х 10-2 х 1,5 = 6 х 10-2 (м) = 6 (см). Відповідь: товщина пластинки 6 см. |
2.
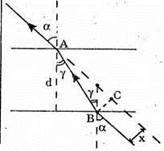
Дано: α = 60º D = 2 см = 2 x 10-2 м Nc = 1,5 Nb = 1,33 Nn = 1 X – ? | Розв’язання:
Розглянемо трикутник ABC. Зміщення x дорівнює довжині катета ВС. Тоді х = AB sin(a – γ), де Отже, Із закону Снелліуcа:
Таким чином:
Перевіримо одиницю фізичної величини: [х] = м. Знайдемо числове значення:
Якщо пластинка розташована у воді:
Знайдемо числове значення:
Відповідь: зміщення променя, який вийшов з пластини в повітрі 1,02 см, а в воді 5,3 мм. |
3.
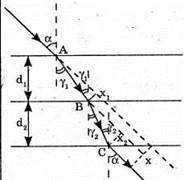
Дано: D1= 16 мм = 1,6 x 10-2 м n1 = 1,5 D2 = 24 мм = 2,4 x 10-2 м N2 = 1,8 α = 48° X – ? | Розв’язання:
Зміщення променя після виходу із пластинок складається із зміщення після проходження першої пластинки х1 та після проходження другої: х = x1 – х2. З властивості прямокутного трикутника: х1 = AB sin(a – γ1);
Отже, Із закону Снелліуса: Знайдемо аналогічно х2: х2 = ВС sin (α – γ2); Отже, Таким чином: Перевіримо одиницю фізичної величини: [х] = м + м = м. Знайдемо числові значення:
Відповідь: зміщення променя становить 1,6 см. |
4.
Рис. з впр. 29.2.
Зміщення променя після виходу з плоско-паралельної пластинки пов’язане з її товщиною співвідношенням:
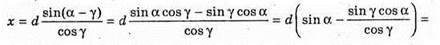
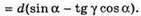
Оскільки (sin a – tg γ cos α) < 1, то x < d.
Зміщення променя не може бути більшим за товщину пластинки.
5.
Дано:
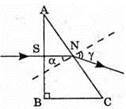
N = 1,5 α0 – ? α – ? | Розв’язання: При падінні світла із оптично більш густого середовища на меншу з оптично менш густині середовищем повністю відбивається, якщо кут падіння променя більший за граничний кут повного відбивання α0.
Знайдемо кут падіння променя:
Знайдемо числові значення: α = 90º – 60° = 30º;
Оскільки α < α0, то промінь заломиться. Відповідь: промінь заломиться. |
6.
Дано: N = 1,5 А – ? | Розв’язання: Рис. з впр. 29.5. Найменший кут падіння променя із оптично більш густого середовища на меншу з оптично менш густим середовищем, при якому відбувається повне відбивання, знаходиться із співвідношення:
Оскільки Відповідь: найменше значення заломного кута становить 41,8°. |
7.
Дано: α1=50°
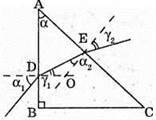
N = 1,5 γ2- ? | Розв’язання:
Згідно з законом Снелліуса: Sin γ2 = n sіn α2. Отже, γ2 = arcsin(n sin α2). З рисунка видно, що Оскільки
Знайдемо γ1із закону Снелліуса:
Знайдемо числові значення: α2 = 60° – 30,71° = 29,29°. У2 = arcsin(1,5 sin 29,29°) = arcsin(1,5 х 0,4892) = 47,2°. Відповідь: промінь вийде під кутом 47,2°. |
8.
Дано:
N = 1,6 φ1 – ? φ21 – ? | Розв’язання:
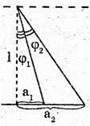
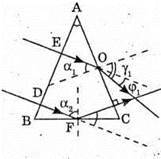
А) У першому випадку відхилення від початкового напряму дорівнює: φ1 = γ1 – α1. З подібності трикутників ADO і EDO:
Із закону Снелліуса: Sin γ1 = n sin α1; γ2 = arcsin(n sin a1). Знайдемо числові значення: γ1 = arcsin(1,6 x x sin 20º) = arcsin 0,547 = 33°; φ1 = 33º – 20° = 13°. Б) Оскільки сума кутів трикутника дорівнює 180°, то A Отже, кут падіння променя на основу дорівнює: Граничний кут повного відбивання для скла:
Оскільки α2 > α0, то падаючий на основу промінь зазнає повного відбивання і вийде з призми під кутом 90°. Згідно із законом відбивання світла: промінь відіб’ється від основи під кутом α2. Отже, відхилення від негативного положення дорівнює: φ2 = (90° – α2) х 2. Знайдемо числове значення: φ2= (90° – 80°) х 2 = 20°. Відповідь: а) промінь відхилиться на 13° вниз; б) промінь відхилиться на 20° вгору. |
9.
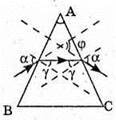
Дано: N = 1,56 γ = 90º
| Розв’язання:
Оскільки сума кутів трикутника дорівнює 180º, то
Отже, Із закону Снелліуса: Отже, Знайдемо числове значення:
Відповідь: заломлений кут призми 39,87°. |
10.
Дано:
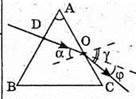
N = 1,5 φ- ? | Розв’язання:
Кут відхилення променя дорівнює: φ = γ – α. Кут падіння променя на грань АС дорівнює:
Оскільки сума кутів трикутника дорівнює 180°, то
Із закону Снелліуса: γ = arcsin(n sin α). sin γ = η sin α; Знайдемо числові значення: γ = arcsin(1,5 sin 3°) = arcsin(1,5 x 0,0523) = 4,5°; φ = 4,5° – 3° = 1,5°. Відповідь: призма відхиляє промінь на 1,5°. |
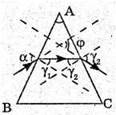
11.
Дано: φ = 15°
N – ? | Розв’язання:
Із закону Снелліуса: Із рисунку видно, що 180º = 2((90° – γ) – (90° – α) + (180° – φ)) = 2(α – γ) + 180° – φ; 2α – 2γ + 180° – φ = 180°;
Отже, Знайдемо числове значення:
Відповідь: показник заломлення матеріалу лінзи 1,3. |
12.
Дано:
| Розв’язання:
З рисунка видно, що Отже, Знайдемо числове значення:
Відповідь: заломлений кут призми |
Вправа 30
1.
Дано: F1 = 20 см = 0,2 м Nс = 1,5 Nв = 1,33 F2 – ? | Розв’язання: Фокусна відстань двоопуклої лінзи пов’язана з абсолютними показниками заломлення речовин середовища та лінзи співвідношенням: Оскільки показник заломлення повітря nп = 1, то для лінзи в повітрі: Аналогічно для лінзи, що знаходиться у воді:
Тоді Перевіримо одиницю фізичної величини: [F2] = м. Знайдемо числове значення:
Відповідь: фокусна відстань лінзи, зануреної у воду, становить 78 см. |
2.
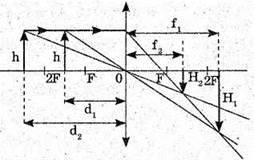
Дано: L = 90 см = 0,9 м Н1 = 4R2 | Розв’язання:
Запишемо формулу тонкої лінзи для першого та другого випадків: Оскільки f1 + d1= l, f2 + d2 = l, то f1 = l1, f2 = l – d2 Тоді формули тонкої лінзи можна переписати:
З іншого боку: Звідси f1d1 = f2d2; З подібності трикутників, що утворені променями, які проходять через оптичний центр лінзи:
Отже, Підставимо отримане значення в систему (1):
L – d1 = 2l – 4d1; Перевіримо одиниці фізичних величин: [F] = м. Знайдемо числове значення: Відповідь: фокусна відстань лінзи 20 см. |
3.
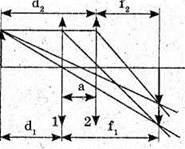
Дано: L А F – ? | Розв’язання: Оскільки в обох випадках отримані зображення дійсні, то формула тонкої лінзи має вигляд:
З рисунка видно, що f1 + d1= l, f2 + d2 = l, d2 = d1 +aα· Оскільки f1= l – d1, f2 = l – d2 = I – d1 – а, то
Розв’яжемо систему рівнянь відносно d1:
D1(l – d1) = (d1 + a)( l – d1 – a); 2d1a = a(l – a);
Підставимо отримані значення в формулу тонкої лінзи:
|
4.
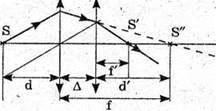
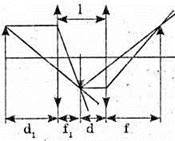
Дано: F = 3 см = З х 10-2 м D = 4 см = 4 х 10-2 м Δ = 3 см = 3 x 10-2 м F′ – ? | Розв’язання:
Зображення S”, яке дає перша лінза, є уявним джерелом для другої лінзи. Знаходимо положення цього зображення з формули тонкої лінзи: Отже, Оскільки відстань від уявного джерела до другої лінзи: D = Δ – f, то з формули тонкої лінзи:
Перевіримо одиниці фізичних величин:
Знайдемо числові значення:
Відповідь: світла, точка знаходиться на відстані 2,25 см від другої лінзи. |
5.
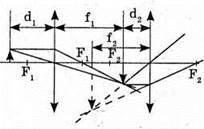
Дано: F1 = 12 см = 0,12 м F2 = 15 см = 0,15 м L = 36 = 0,36 D1 = 48 см = 0,48 м F – ? | Розв’язання:
Знайдемо положення зображення, яке дає перша лінза, з формули тонкої лінзи: Оскільки d = l – f1, то формула тонкої лінзи:
Перевіримо одиниці фізичних величин:
Знайдемо числові значення:
Відповідь: зображення предмету знаходиться на відстані 60 см від другої лінзи. |
6.
Дано: F1 = 12,5 см = 0,125 м F2 = -10 см = -0,1 м Fz = 5 см = 0,05 м | Розв’язання: Оптична сила системи контактуючих тонких лінз дорівнює сумі оптичних сил окремих лінз: D = D1 + D2 + D3. Оскільки оптична сила лінзи – де величина обернено пропорційна фокусній відстані, то:
Отже, Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: фокусна відстань об’єктива 5,6 см. |
7.
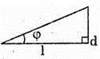
Дано: L = 8 м φ = 2′ D – ? | Розв’язання:
З властивості прямокутного трикутника d = l sin φ. Перевіримо одиницю фізичної, величини: [d] = м. Знайдемо числові значення: від (2′) = 0,0006. D = 8 х 0,0006 = 0,005 (м) = 5 (мм). Відповідь: поділки мають бути на відстані не менше 5 мм. |
8.
Дано: L = 18 см = 18 x 10-2 м F1 = 2 мм = 2 x 10-3 м F2 = 40 мм = 4 x 10-2 м L = 25 см = 25 x 10-2 м Г – ? | Розв’язання:
Як видно з рисунку мікроскоп дає уявне, збільшене, перевернуте зображення. Збільшення системи дорівнює добутку збільшень лінз, що її складають: Г = Гоб х Гок. Збільшення об’єктиву дорівнює:
Збільшення окуляру дорівнює: Де l – відстань найкращого зору. Отже, збільшення мікроскопу: Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: мікроскоп дає збільшення в 563 рази. |
9.
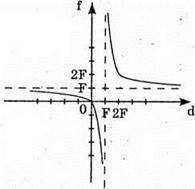
Залежність відстані між зображенням та лінзою від відстані між предметом та лінзою описується формулою тонкої лінзи: 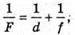
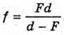 Знайдемо точки перетину з віссю
Знайдемо точки перетину з віссю 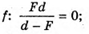 Fd = 0; d = 0.
Fd = 0; d = 0.
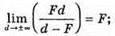 пряма f = F – горизонтальна асимптота.
пряма f = F – горизонтальна асимптота.
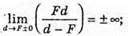 пряма d = F – вертикальна асимптота.
пряма d = F – вертикальна асимптота.
10.
Лінійне збільшення дорівнює: 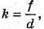 де f – відстань від зображення до лінзи.
де f – відстань від зображення до лінзи.
А) Формули тонкої лінзи: 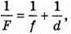
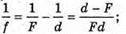
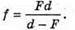 Отже,
Отже, 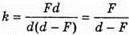
Б) Якщо d < F, то лінза дає уявне зображення: 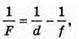
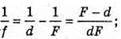
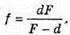
Отже, 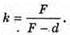
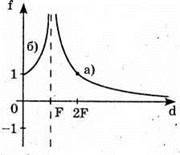
При d > F: 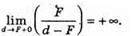
При d < F: 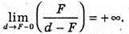
Отже, пряма d = F – вертикальна асимптота.
Вправа 31
1.
Дано: L1 = 1м Е1 = Е2
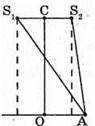
Δl – ? | Розв’язання: Згідно з законом освітленості від точкового джерела:
Оскільки сила світла зменшилася вдвічі, то Отже, Перевіримо одиницю фізичної величини: [l2] = м. Знайдемо числове значення:
Відповідь: екран слід наблизити на 30 см. |
2.
Дано:
R = 1,5 х 108 км = = 1,5 х 1011 м R = 7 х 105 км = 7 х 108 м E – ? | Розв’язання: Будемо вважати, що Сонце – це плоских диск, який випромінює в двох напрямках. Тоді його яскравість визначається з формули Оскільки площа кола S = πR2, то Звідси Освітленість поверхні визначається з формули: Де α – кут падіння променів відносно нормалі до поверхні. За умовою задачі cos α = 1. Тоді Перевіримо одиницю фізичної величини:
Знайдемо числові значення:
Відповідь: освітленість поверхні Землі 4,1 х 104 лк. |
3.
Дано: I1 = 75 кд I2 = 25 кд R1= Зг2
| Розв’язання: Освітленість поверхні першою лампою: А другою: Тоді Перевіримо одиницю фізичної величини: Знайдемо числове значення: Е2 = ЗE1 Відповідь: освітленість збільшиться в 3 рази. |
4.
Дано: Е1 = 2E2 α – ? | Розв’язання: Освітленість площини під час перпендикулярного падіння променів: Освітленість, тієї ж площини при падінні на неї променів Під кутом α: Звідси Оскільки Відповідь: площину треба відхилити на 60º. |
5.
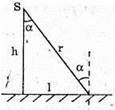
Дано: I = 500 кд H = 3 м L = 4 м E – ? | Розв’язання:
Освітленість поверхні на відстані lі від основи стовпа:
З теореми Піфагора: r2 = h2 +l2; З властивості прямокутного трикутника Тоді Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: освітленість поверхні 12 лк. |
6.
Дано: R = 85 см = 0,85 м S0 = 1,5 м2 Ф0 = 360 лм I – ? Ф – ? | Розв’язання: Оскільки сила світла точкового джерела чисельно дорівнює світловому потоку, який це джерело створює в тілесному куті, то Тілесний кут дорівнює Отже, Повний світовий потік дорівнює: Ф = 4πI Перевіримо одиниці фізичних величин: [Ф] = ср х кд = лм. Знайдемо числові значення:
Ф = 4 х 3,14 х 173 = 2,2 х 103 (лм). Відповідь: сила світла точкового джерела 173 кд, повний світловий потік 2,2 лм. |
7.
Дано: Е = 9500 лк S = 1,6 м2 Ф – ? | Розв’язання: Оскільки освітленість – це світловий потік, що припадає на одиницю площі освітленої поверхні: Перевіримо одиницю фізичної величини: [Ф] = лк х м2 = лм. Знайдемо числове значення: Ф = 9500 х 1,6 = 15,2 х 103 (лм). Відповідь: на поверхню стола попадає світловий потік 15,2 х 103 лм. |
8.
Дано: D = 1,2 м H = 1,2 м Ф = 750 лм Е – ? | Розв’язання:
Освітленість краю стола дорівнює: Оскільки повний світловий потік: Ф = 4πI, то З теореми Піфагора: З властивості прямокутного трикутника: В результаті отримаємо:
Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
|
9.
Дано: E1 = E2 L = 2,4 м I1 = 100 кд І2 = 50 кд L1 – ? | Розв’язання:
Освітленість, що створює перша лампа, дорівнює: А освітленість, що створює друга лампа: Для того, щоб екран був однаково освітлений з обох боків: З рисунку видно, що l = l1 + l 2. Тоді l2 =l – l 1
Оскільки I1= 2I2, то Розв’яжемо квадратне рівняння відносно L1: D = 16l2 – 8l2 = 8l2. Перевіримо одиницю фізичної величини: [l1] = м.
Знайдемо числове значення:
Не відповідає умові задачі, бо отримане значення перевищує відстань між лампами.
Відповідь: екран потрібно розмістити на відстані 1,4 м від лампи 100 кд. |
10.
Дано: І = 400 кд L 1 = 1 м Е = E1 + 100 лк L2- ? | Розв’язання:
Освітленість екрана створюється променями, що падають від джерела та променями, що падають після відбиття від дзеркала: Е = Е1 + Е2. Згідно з умовою задачі Е = Е1 + 100 кд. Отже, E1 + Е2 = E + 100 кд, Е2 = 100 кд. Освітленість, що створюють відбиті промені, дорівнює освітленості, які створює зображення лампи S’: Отже, Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: дзеркало потрібно поставити на відстані 50 см позаду лампи. |
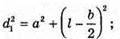
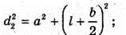
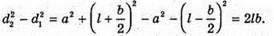
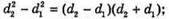
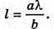
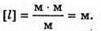
 class=""/>
class=""/>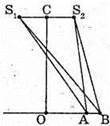
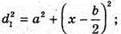
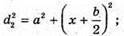
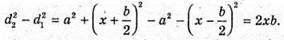
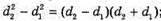
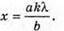
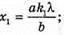
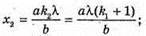
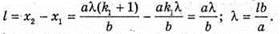
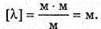
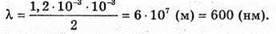
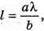
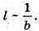
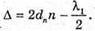
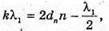
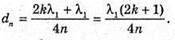
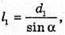
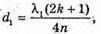
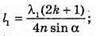
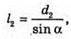
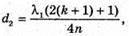
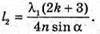
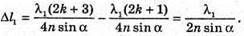
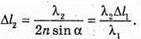
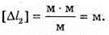
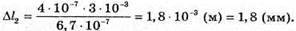
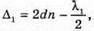
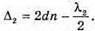
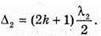
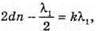 (1)
(1) 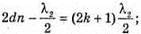
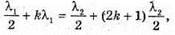
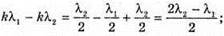
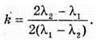
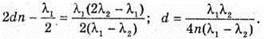
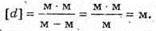
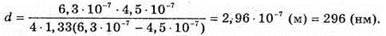
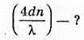
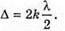
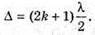
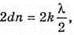
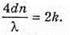
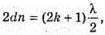
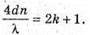
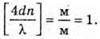
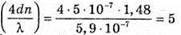 – непарне число.
– непарне число.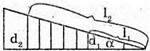
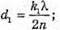 2d2n = k2λ,
2d2n = k2λ, 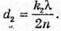
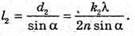
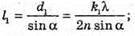
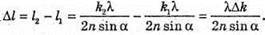
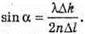
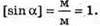
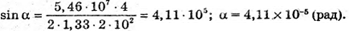
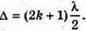
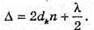
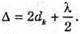
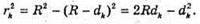
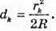
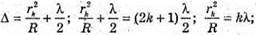
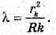
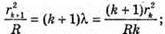
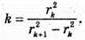
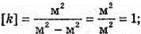
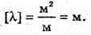
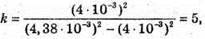 (k + 1) = 5 + 1 = 6;
(k + 1) = 5 + 1 = 6;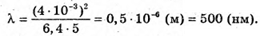
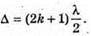
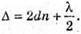
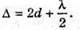
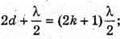 2d = кλ;
2d = кλ; 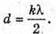
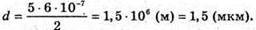
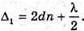
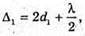
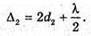
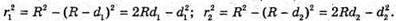
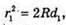
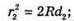
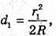
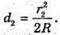
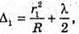
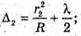
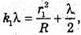
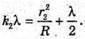
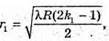
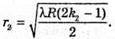
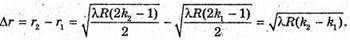
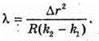
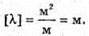
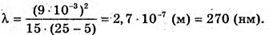
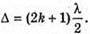
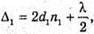
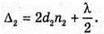
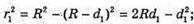
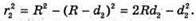
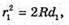
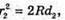
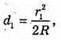
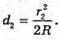
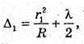
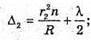
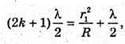
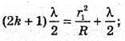
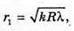
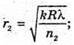
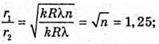 n = 1,252 = 1,56.
n = 1,252 = 1,56.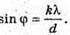
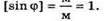
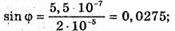
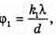 k2λ = dφ2,
k2λ = dφ2, 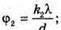
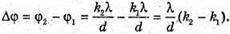
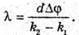
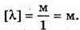
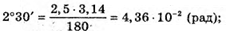
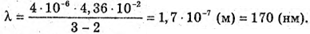
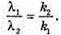
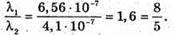
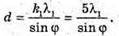
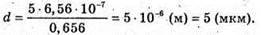
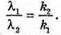
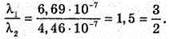
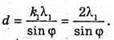
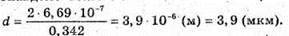
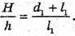
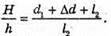
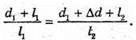
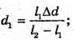
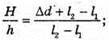
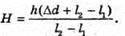
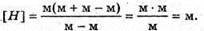
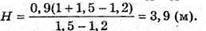
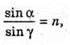
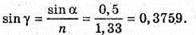
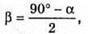 то
то 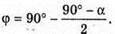
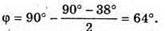
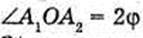 навколо ребра двогранного кута.
навколо ребра двогранного кута.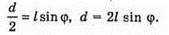
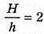
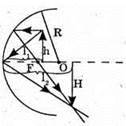
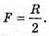
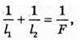
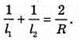
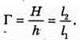
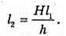
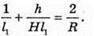
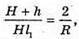
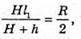 Н = 2 h,
Н = 2 h,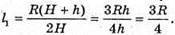
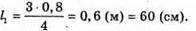
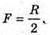
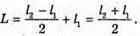
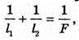
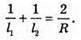
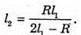
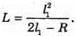
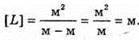
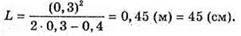
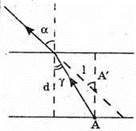
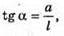
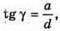 а = d tg γ.
а = d tg γ.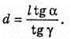 `
`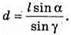
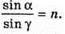
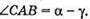
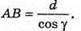
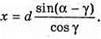

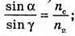
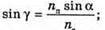
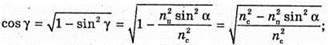
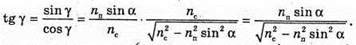
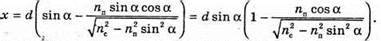
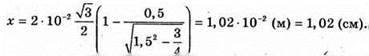
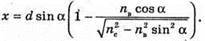
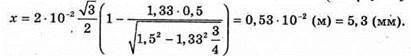
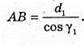
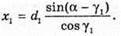
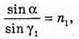
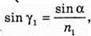
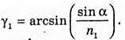
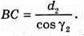
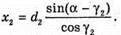
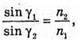
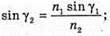
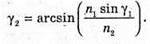
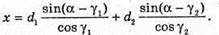
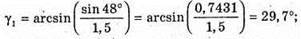
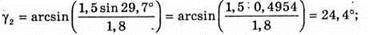
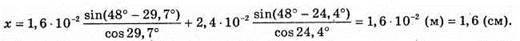
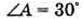
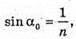

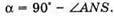
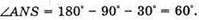
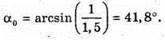
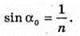
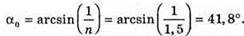
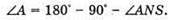
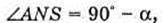 То
То 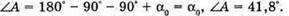

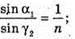
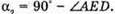 . Оскільки сума кутів трикутника дорівнює 180°, то з трикутника ADE знайдемо
. Оскільки сума кутів трикутника дорівнює 180°, то з трикутника ADE знайдемо 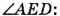
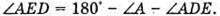
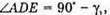 το
το 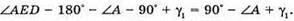
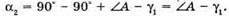
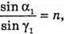
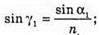
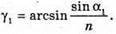
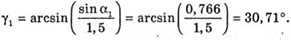
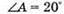
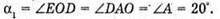
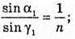
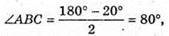
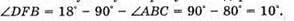
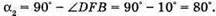
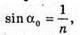
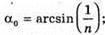
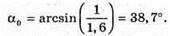
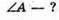
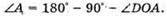
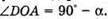
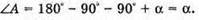
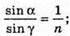
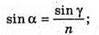
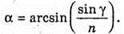
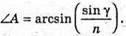
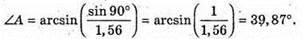
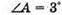
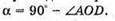
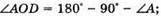
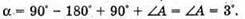
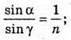
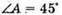
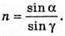
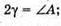
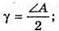
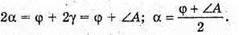
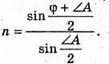
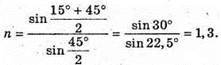
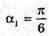
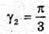
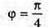
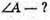
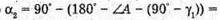
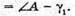
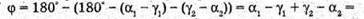
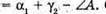 Отже,
Отже, 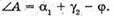
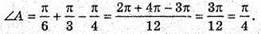
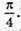
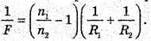
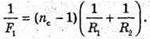
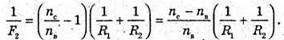
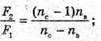
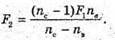
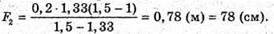
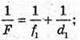
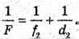
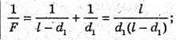
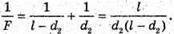 (1)
(1)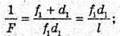
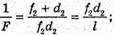
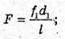
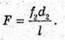
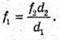
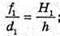
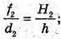
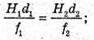
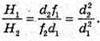
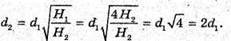
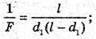
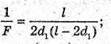
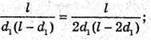
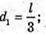
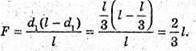
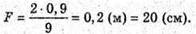
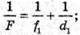
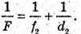
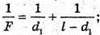
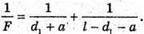
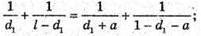
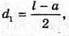
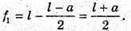
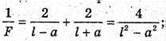
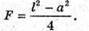
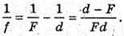
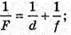
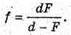
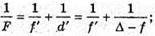
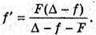
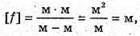
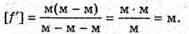
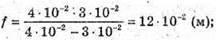
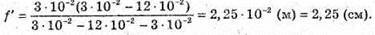
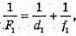
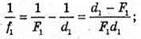
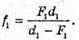
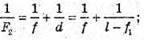
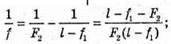
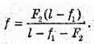
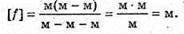
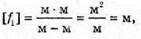
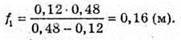
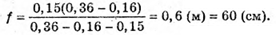
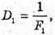
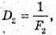
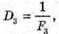
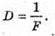
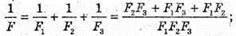
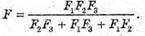
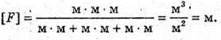
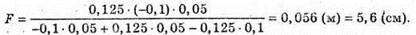
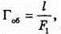 де l – оптична довжина тубуса мікроскопа, яка дорівнює відстані між головними фокусами об’єктива та окуляра (l ≈ f1).
де l – оптична довжина тубуса мікроскопа, яка дорівнює відстані між головними фокусами об’єктива та окуляра (l ≈ f1).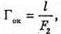
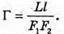
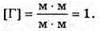
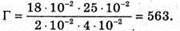
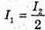
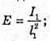
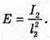
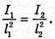
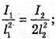
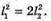
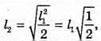
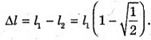
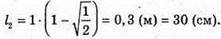
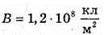
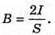
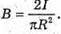
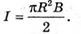
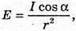
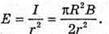
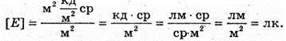
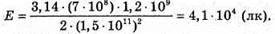
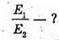
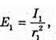
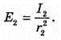
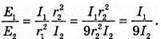
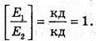
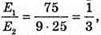
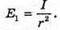
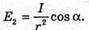
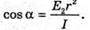
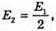 то α = 60º.
то α = 60º. 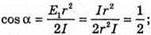
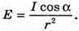
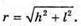
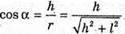
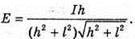
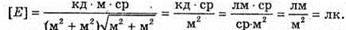

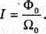
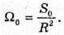
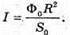
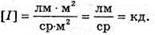
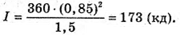
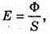 то Ф = ES.
то Ф = ES.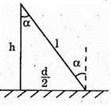
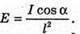
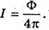
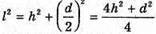
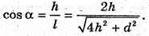
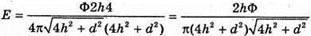
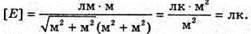
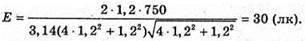 30 лк.
30 лк.