Задачі на спільну роботу
Задачі на спільну роботу
1
Розв’яжи задачу 1. Зістав задачі 1 і 2. Що змінилось? Як ця зміна вплине на розв’язання задачі 2?
□ 1) 24 т води перший насос накачує за 6 год, а другий – за 3 год. Скільки тонн води накачають за 1 год два насоси, якщо працюватимуть разом?
□ 2) 24 т води перший насос накачує за 6 год, а другий – за 3 год. За скільки годин накачають 24 т води два насоси, якщо працюватимуть разом?
Учні виконали схеми до задачі 2. Чи можна з ними погодитись? Поясни, що позначає кожний відрізок. Поясни розв’язання задачі 2 за
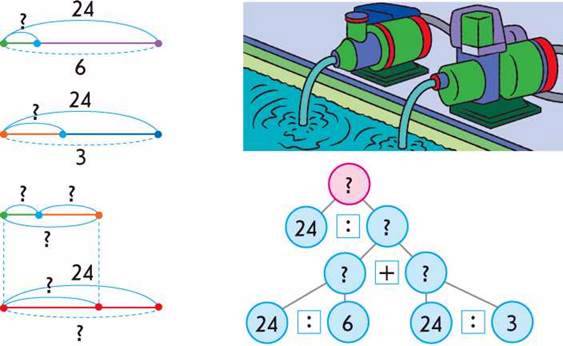
Сергійко змінив ситуацію задачі 2 і отримав задачу 3. Хлопчик вважає, що ця зміна жодним чином не вплине на розв’язання – в ньому треба лише змінити пояснення. Чи можна погодитись із Сергійком? Поясни розв’язання задачі 3.
□ 3) 24 деталі перший робітник виготовляє за 6 год, а другий – за 3 год. За скільки годин виготовлять 24 деталі 2 робітники, якщо працюватимуть разом?
План розв’язування задач на спільну роботу
Поліна змінила числові дані в задачі 3 і отримала задачу 4. Як ця зміна вплине на розв’язання задачі 4? Розв’яжи задачу 4.
□ 4) 36 деталей
Зістав задачі 2-4. Що спільне в їх розв’язанні? Що є “ключем” до розв’язання задач цього виду?
Задачі на спільну роботу
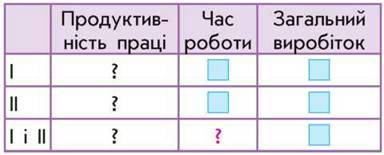
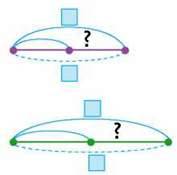
План розв’язування
1. Визначаю продуктивність першого виконавця дією ділення.
2. Визначаю продуктивність другого виконавця дією ділення.
3. Визначаю продуктивність спільної роботи дією додавання.
4. Визначаю час спільної роботи дією ділення.
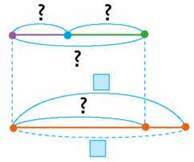
2
Знайди значення виразів.
56000 + 48000 330000 – 250000 960000 : 24
68000 : 34000 32000 ∙ 4 11200 : 28
329000 + 230000 564000 – 323000 8 ∙ 38000
720000 : 12000 72000 : 18 9000 + 6000
36000 + 27000 63000 – 58000 7400 + 1800
Задачі на спільну роботу
1
Склади задачу за таблицею. Перевір її розв’язання.
Продуктивність праці | Час роботи | Загальний виробіток | |
І | ? | 4 | 96 |
ІІ | ? | 6 | 96 |
І і ІІ | ? | ? | 200 |
1) 96 : 4 = 24
2) 96 : 6 = 16
3) 24 + 16 = 40
4) 200 : 40 = 5
Або:
200 : (96 : 4 + 96 : 6) = 5
Толя склав обернені задачі. Досліди, як зміна шуканого впливає на розв’язання.
Перша обернена задача
Продуктивність праці | Час роботи | Загальний виробіток | |
І | ? | 4 | 96 |
ІІ | ? | 6 | 96 |
І і ІІ | ? | 5 | ? |
Друга обернена задача
Продуктивність праці | Час роботи | Загальний виробіток | |
І | ? | 4 | 96 |
ІІ | ? | ? | 96 |
І і ІІ | ? | 5 | 200 |
Третя обернена задача
Продуктивність праці | Час роботи | Загальний виробіток | |
І | ? | 4 | 96 |
ІІ | ? | 6 | ? |
І і ІІ | ? | 5 | 200 |
Четверта обернена задача
Продуктивність праці | Час роботи | Загальний виробіток | |
І | ? | ? | 96 |
ІІ | ? | 6 | 96 |
І і ІІ | 5 | 5 | 200 |
Задачі на спільну роботу / обернені до них
План розв’язування
1. Визначаю продуктивність виконавця.
2. Визначаю продуктивність виконавця/спільну продуктивність.
3. Визначаю спільну продуктивність/продуктивність виконавця.
4. Відповідаю на запитання задачі.
Прямі та обернені задачі
2
Згадай відомі тобі розрядні одиниці. Як помножити число на 10? на 100? Як розділити число на 10? на 100? У кожному стовпчику знайди значення перших двох виразів. Чи можна міркувати так само, щоб знайти значення решти виразів? Знайди їх значення.
6 ∙ 10
6 ∙ 100
6 ∙ 1000
6 ∙ 10000
6 ∙ 100000
800000 : 10
800000:100
800000:1000
800000:10000
800000:100000
Щоб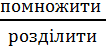 
число на розрядну одиницю 10; 100; 1000; 10000; 100000, достатньо справа від цього числа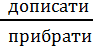 
Стільки нулів, скільки їх у розрядній одиниці.
3
Знайди значення виразів, користуючись правилом.
7 ∙ 100000 32 ∙ 10000 176 ∙ 1000
5800 : 10 400000 : 1000 74000 : 100
3456 ∙ 100 260000 : 1000 8652 ∙ 10
480000 : 100 478 ∙ 1000 500000 : 10
234 ∙ 1000 900000 : 1000 400 ∙ 100
4
Розв’яжи задачу. Склади та розв’яжи хоча б одну обернену задачу.
□ Гончар може виготовити 12 глечиків за 3 години, а його учень – за 6 годин. Скільки глечиків можуть виготовити майстер і учень за 2 години, працюючи разом?
(1 votes, average: 5.00 out of 5)
Loading...