Задачі на знаходження відстані за даними швидкістю і часом. Знаходження значень виразів на додавання і віднімання (№№ 500-509)
Тема. Задачі на знаходження відстані за даними швидкістю і часом. Знаходження значень виразів на додавання і віднімання (№№ 500-509).
Мета. Ознайомити учнів із способом визначення відстані за відомими швидкістю і часом; формувати вміння розв’язувати задачі на основі творчих видів роботи; розвивати обчислювальні навички.
Обладнання. Таблиця усних обчислень; “Картки для поточного контролю знань”; таблиця “Швидкість. Відстань Час”.
Зміст уроку
І. Контроль, корекція і закріплення знань.
1. Перевірка домашнього завдання.
А)
Б) Зачитати відповідь до задачі № 499. (Вершник їхав зі швидкістю 10 км/год.)
2. Завдання для опитування.
А) Скласти і розв’язати задачі за таблицею.
Рухомий об’єкт | Швидкість | Час | Відстань |
Лижник | ? | 4 год | 48 км |
Катер | 7 | 3 год | 96 км |
Б) Виконання завдань із “Карток для поточного контролю знань”.
1- а група – № 61 (с. 35);
2- а група – № 62 (с. 35).
3. Усні обчислення.
Гра

II. Вивчення нового матеріалу.
1. Задача.
Лижник був у дорозі 3 години і подолав відстань 39 км. З якою швидкістю рухався лижник?
(39 : 3 = 13 (км/год).)
– Складіть обернену задачу до даної, в якій потрібно відшукати число 39.
Швидкість | Час | Відстань |
13 км/год | 3 год | ? |
– Як знайти відстань, яку подолав лижник?
(13 • 3 = 39 (км).)
Висновок. Щоб знайти відстань, треба швидкість помножити на час.
2. Первинне закріплення.
А) Задача № 501.
– Про що йдеться в задачі?
– Повторіть задачу за таблицею.
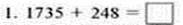
– Складемо план розв’язування задачі.
1) Яку відстань пройшов пасажирський катер?
2) Яку відстань пройшов буксирний катер?
3) На скільки кілометрів більше пройшов буксирний катер, ніж пасажирський?
(Розв’язання:
1) 24 • 4 = 96 (км);
2) 14 • 7 = 98 (км);
3) 98 – 96 = 2 (км).)
Б) За даними таблиці вправи № 502 знайти відстані.
Завдання виконують усно.
В) Задача № 503.
– Повторіть задачу за таблицею.
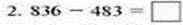
– Самостійно розв’яжіть задачу.
(Розв’язання: 4 • 2 + 45 • 3 = 143 (км).)
Фізкультхвилинка.
III. Розвиток математичних знань.
1. Виконання завдання № 504.
1- ий стовпчик – колективно:
2- ий – самостійно.
Результати обчислень учні звіряють із записаними на дошці відповідями.
48350 – 9405 + 598 = 39543;
8365 – (2120 + 1080) = 5165.
2. Задача № 505. За умовою задачі учні ставлять різні запитання і усно розв’язують їх.
3. Розв’язування задачі № 506.
На дошці – таблиця із даними задачі.
Рухомий об’єкт | Швидкість | Час | Відстань |
Велосипедист | ? км/год? | 12 год | 180 км |
Мотоцикліст | ? на 36 км/год більше | 20 год | ? км |
– Що відомо про рух велосипедиста? (Час руху і відстань.)
– Про що звідси можна дізнатися? (Про швидкість руху велосипедиста.)
– Що відомо про рух мотоцикліста? (Відомий час руху; можемо знайти швидкість руху мотоцикліста.)
– Чи можемо знайти відстань, яку проїде мотоцикліст?
– Розв’язання запишіть самостійно окремими діями.
(Розв’язання:
1) 180 : 12 = 15 (км/год) – швидкість велосипедиста;
2) 15 + 36 = 51 (км/год) – швидкість мотоцикліста;
3) 51 • 20 = 1020 (км) – проїде мотоцикліст.)
4. Цікава задача.
Собака женеться за кроликом, який знаходиться за 630 футів від нього. Він робить стрибок у 9 футів щоразу, коли кролик стрибає на 7 футів. Скільки стрибків має зробити собака, щоб наздогнати кролика? (Фут ≈ 30 см.)
(Розв’язання: 630 : (9 – 7) = 315 (стр.)
Відповідь: 315 стрибків.)
IV. Підсумок уроку.
– Як знайти відстань?
V. Домашнє завдання.
№№ 508, 509 (с. 82).