Застосування різних способів розкладання багаточленів на множники
Урок № 54
Тема. Застосування різних способів розкладання багаточленів на множники
Мета: відпрацювати навички застосування спеціальних прийомів та класичних методів розкладання багаточленів на множники; продовжувати знайомство учнів зі сферою застосування розкладання багаточленів на множники; узагальнити та систематизувати набуті з теми знання та уміння і навички.
Тип уроку: комбінований.
Хід уроку
I. Організаційний момент
Перевіряємо готовність учнів до уроку, повідомляємо план роботи.
II. Перевірка домашнього
@ Запропоноване домашнє завдання не є простим для учнів, тому слід перевірити його ретельно; учні ставлять запитання та разом з учителем шукають відповіді на них.
Особливу увагу звертаємо на завдання № 1 (3, 4, 5) та 2 (4), бо в № 1 (3) маємо різницю кубів (не зовсім знайоме, принаймні на попередньому уроці таких завдань не було).
№ 1 (4) – маємо одразу два повні квадрати (нове!).
№ 1 (5) – традиційно складне, бо треба “побачити” вираз, протилежний повному квадрату.
№ 2 (4) – обов’язково розібрати, бо містить такий контрольний момент: ділення на вираз зі змінною звужує ОДЗ рівняння, а отже,
III. Формулювання мети й завдань уроку
@ Згідно з визначеним на першому уроці планом, на цьому відпрацьовуємо навички застосування різних способів та прийомів розкладання багаточленів на множники та розширюємо сферу застосування набутих умінь і навичок, а також узагальнюємо та систематизуємо свій досвід.
IV. Актуалізація опорних знань
Фронтальна бесіда
1. Що означає розкласти багаточлен на множники?
2. Які способи розкладання багаточленів на множники ви знаєте?
3. Які з названих способів розкладання багаточленів на множники і в якому порядку використаєте, щоб подати у вигляді добутку такі вирази:
1) х2 – ху;
2) х2 – у2;
3) х3 – х;
4) х2 – 2х + 1;
5) х3 – 2х2 + х;
6) х2 – 2х + 1 – у2;
7) х2 – у2 + 2х – 2у;
8) х3 – х2 + х – 1;
9) (х – 1)2 – х2?
V. Робота з випереджальним домашнім завданням
Завдання 1. Виділіть повний квадрат у виразах:
1) х2 + 2х – 8;
2) а2 – 8а + 12;
3) 4с2 – 4с – 3;
4) х2 – 6ху + 5у2;
5) а2 + 12аb + 11b2;
6*) (х – 1)2 – 6(х – 1) + 8.
Завдання 2. Подайте вираз, що стоїть після повного квадрата, у вигляді квадрата деякого виразу. Прочитайте вираз, що утворився. Що спільного мають дані вирази? Як їх розкласти на множники?
Зробіть висновки.
@ Якщо вся підготовча робота належно проведена, то висновок, який роблять учні, може бути приблизно таким, до якого хоче підвести учнів учитель, а саме: щоб розкласти тричлен на множники за формулою різниці квадратів двох виразів, можна використати прийом “виділення повного квадрата двочлена”.
Завдання 3. Розкладіть дані тричлени на множники:
1) х2 + 6х + 8;
2) х2 + 12х + 35;
3) х2 – 10х – 24;
4*) х2 – 7х + 12.
(4*) – контрприклад – у цьому тричлені зручніше розбити -7х на два доданки і згрупувати, бо -7х має непарний коефіцієнт.)
VI. Засвоєння вмінь та навичок
@ Розв’язуємо вправи достатнього та високого рівнів складності. Якщо рівень підготовки учнів досить високий і відповідний темп виконання, то можна запропонувати кілька специфічних прийомів роботи з виразами: перегрупування тощо.
Виконання письмових вправ
1. Розкладіть на множники:
1) х2 – 4х + 3;
2) х2 + 2х – 8;
3) t2 + t – 6;
4) k4 + 6k2 + 5;
5) u4 + 2u2 – 35;
6) (3×2 – 4)2 – 8(3×2 – 4) – 9.
2. Розкладіть на множники:
1) (х – у)(х + у) + 2(2х – у) + 3;
2) (х – у)(х + у) + 2(3х – 2у) + 5.
3. Розв’яжіть рівняння:
1) х2 – 8х + 7 = 0;
2) у2 + 12у + 20 = 0;
3) (х – 1)2 + 6(х – 1) + 8 = 0;
4) (х – 1)(х – 3)(х2 – 3) = (x – 1)(х – 3).
4. Доведіть, що значення виразу 334 + 992 – 330 – 990 ділиться на 80.
5*. Відомо, що а + b = 5, ab = 4. Знайдіть значення виразу:
1) a2b + ab2; 2) a2 + b2; 3) a3 + b3.
VII. Підсумки уроку
@ Найважливішим підсумком є формування в учнів правильного розуміння: 1) будови системи форм та методів (способів) розкладання багаточленів на множники; 2) сфери застосування названих понять та способів дій на уроках математики (або там, де мова йде про математичні об’єкти: числові та буквені вирази, рівняння тощо).
Тому бажано цей етап уроку присвятити саме систематизації та узагальненню знань та вмінь учнів.
Учитель може підготувати заздалегідь (або робити записи під час бесіди) картки із записами основних понять з теми “Розкладання на множники”: винесення спільного множника за дужки і т. д.
Учитель пропонує учням назвати основні математичні поняття, що засвоюються в ході вивчення цієї теми (для пожвавлення роботи можна улаштувати “Математичний аукціон” – див. математика, 6 кл.), і відповідно відкриває картки (або робить запис на дошці).
Після того як будуть названі усі поняття, пропонуємо учням розташувати ці картки в порядку, що відповідає логіці теми (послідовність застосування способів тощо), і класифікуємо види завдань, що були розв’язані в цій темі. Врешті-решт можна всі міркування подати у вигляді схеми:
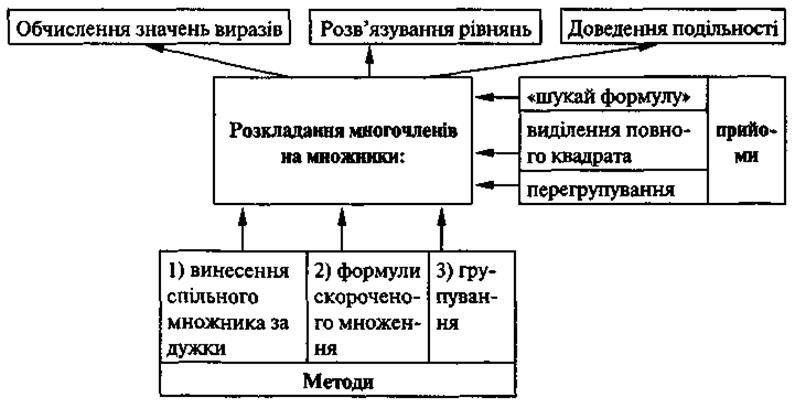
VIII. Домашнє завдання. Домашня самостійна робота
№ 1. Розкладіть на множники:
1) 6а3 – 6а;
2) 2х2 + 24ху + 72у2;
3) а3 – ab – a2b + a2;
4) х2 + 2ху + у2 – 49;
5) а3 + 8 – а2 – 2а;
6) m3 + 27n5 + m2 + 6mn + 9n2;
7) а2 – b2 + 4а + 4;
8) х2 – 2х – 3;
9) х2 + 4х – 5.
№ 2. Розв’яжіть рівняння:
1) х2 – 2х – 35 = 0;
2) х3 – 9 = х – 9х2.
№ 3. Доведіть, що значення виразу 1110 + 4 •749 + 1111 – 4 •748 ділиться на 12.
Додатково: попрацювати зі схемою – див. “Підсумки” (вдосконалення).