Головна ⇒ 📌Довідник з геометрії ⇒ Зрізаний конус
Зрізаний конус
Геометрія
Тіла обертання
Зрізаний конус
Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню – по колу з центром на осі конуса. Така площина відтинає від конуса менший конус. Частина, що залишилась, називається Зрізаним конусом (див. рисунок):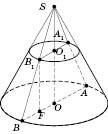
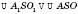 ;
;
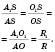
Зверніть увагу на осьовий переріз зрізаного конуса. Це рівнобічна трапеція, в якої основи – діаметри основ зрізаного конуса, бічні сторони – твірні, висота – висота зрізаного конуса.
Отже, 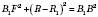 .
.
Sб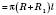 , де
, де 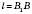 , – формула для обчислення бічної поверхні зрізаного конуса.
, – формула для обчислення бічної поверхні зрізаного конуса.
Related posts:
- Куля, вписана в конус Геометрія Комбінації геометричних тіл Куля, вписана в конус Площина, яка містить вісь конуса, є площиною симетрії (рисунок нижче зліва). Осьовий переріз комбінації є рівнобедреним трикутником, у який вписане коло (рисунок справа). Трикутник – це осьовий переріз конуса, тобто – твірні конуса, AB – діаметр основи конуса, а коло – велике коло вписаної кулі. Отже, радіус […]...
- Конус Геометрія Тіла обертання Конус Круговим конусом називається тіло, яке складається з круга – Основи конуса, точки, яка не лежить у площині цього круга, – Вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи. Відрізки, що сполучають вершину конуса з точками кола основи, називаються Твірними конуса. Конус називається Прямим (далі просто “конус”), якщо […]...
- Конус і зрізаний конус 983. Нехай дано конус, твірна якого AM = l, і нахилена до площини основи під кутом ∠MAO = α. А) ΔAMO – прямокутний. OM – висота, OM = l × sin α; Б) AO – радіус основи конуса. AO = l × cos α; В) ΔAMB – осьовий переріз; Г) площа основи конуса – площа […]...
- Конус, вписаний у кулю Геометрія Комбінації геометричних тіл Конус, вписаний у кулю Вершина конуса лежить на сфері (рисунок нижче зліва). Основа конуса лежить на сфері. Комбінація є симетричною відносно площини, що містить вісь конуса. У такому перерізі дістанемо трикутник, вписаний у коло (рисунок справа). Трикутник рівнобедрений. Бічні сторони – твірні конуса, коло – велике коло описаної кулі. Отже, радіус […]...
- Властивості конуса 1. 1) Твірна конуса не може утворювати з його основою прямий кут, оскільки Вона є гіпотенузою трикутника обертання, яка утворює бічну поверхню конуса. 2) Теж не може (обгрунтування у п. 1). Якщо конус зрізаний 1) ні; 2) так. Відповідь: 1) ні; 2) ні для зрізаного конуса 1) ні, 2) так. 2. Нехай SA – твірна […]...
- Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...
- Конус. Площа поверхні та об’єм конуса УРОК № 57 Тема. Конус. Площа поверхні та об’єм конуса Мета уроку: повторення, приведення в систему й розширення відомостей про конус, площу поверхні та об’єм конуса; формування вмінь учнів знаходити площі поверхонь і об’єми конусів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі конусів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
- ЦИЛІНДР. КОНУС. КУЛЯ Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ § 18. ЦИЛІНДР. КОНУС. КУЛЯ У 5 класі ви вже ознайомилися з просторовими фігурами: прямокутним паралелепіпедом і кубом. ь на малюнок 56. Ви бачите предмети, які використовують у побуті. У сі вони мають одну й ту саму форму – циліндра (мал. 57). Мал. 56 Мал. 57 Мал. 58 Maл. 59 […]...
- Циліндр Геометрія Тіла обертання Циліндр Круговим циліндром називається тіло, яке складається з двох кругів, що не лежать в одній площині й суміщаються паралельними перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (див. рисунок). Круги називаються Основами циліндра, а відрізки, що сполучають точки кіл кругів, – Твірними циліндра. Основи циліндра рівні й лежать у паралельних […]...
- Зрізаний конус – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Зрізаний конус...
- Конуси 1050. ΔSAPO: ∠АОР = 90°, ОЕ = АЕ = ЕР = 6,5 см → АР = 13 см. АО = 5 см. R = AO, L = АР = 13 см, r = 5 см. Sп. к. = πrl + πr2 = π(5 × 13 + 52) = 90π. S = 90π см2. 1051. ΟΑ […]...
- Трапеція Геометрія Чотирикутники Трапеція Трапецією називається чотирикутник, у якого тільки дві протилежні сторони паралельні. Ці сторони називаються Основами трапеції, а дві інші – Бічними сторонами. Трапеція, в якої бічні сторони рівні, називається Рівнобічною (див. рисунок нижче зліва). Якщо одна з бічних сторін трапеції перпендикулярна до основ, трапеція називається Прямокутною (рисунок нижче справа). Теорема 1. Кути трапеції, […]...
- Об’єм конуса і зрізаного конуса 1295. Нехай SA – твірна конуса, ∠SAO = α, SA = l. З ΔSAO : SO = SA × sin ∠SAO = I sin α, AO = AS × cos ∠SAO = І × cos α. Отже, об’єм конуса V дорівнює: Відповідь: 1296. Нехай радіус основи свинцевого конуса дорівнює r, а висота циліндра – H. […]...
- Циліндр, описаний навколо кулі Геометрія Комбінації геометричних тіл Циліндр, описаний навколо кулі Площина, проведена через центр кулі паралельно твірним циліндра (рисунок нижче зліва), є площиною симетрії тіла. У цьому випадку висота циліндра дорівнює діаметру кулі. В осьовому перерізі цього тіла отримаємо прямокутник, у який вписане коло (рисунок справа). Але із цього випливає, що осьовий переріз даного циліндра – квадрат. […]...
- Об’єми круглих тіл Геометрія Об’єми тіл Об’єми круглих тіл Об’єм циліндра (див. рисунок) дорівнює добутку площі його основи та висоти. ; . Об’єм конуса (див. рисунок) дорівнює одній третині добутку площі його основи та висоти. . . Об’єм зрізаного конуса (див. рисунок): ....
- Куб, конус. Креслення розгорток куба, конуса УРОК 2 Тема. Куб, конус. Креслення розгорток куба, конуса Мета: навчити креслити розгортки куба, конуса; вдосконалювати уміння та навички роботи з папером; розвивати конструкторські уміння та навички; прищеплювати любов до праці; виховувати охайність, посидючість, працьовитість, правила естетики. Обладнання: папір, ножиці, клей, пензлик, олівець, гумка, серветка, таблиця для гри “Вгадайте слово”, циркуль. ХІД УРОКУ І. Організаційний […]...
- Тіла обертання 1008. Осьовий переріз – це ΔARB1, де BB1 = 2 × СВ = 4 (см), АС + В 1В, В 1C = СB. S = 4 см2. 1009. Sб. ц. = 2πrh = 2π × 2 × 10 = 40π (см2), Sб = 40π см2. 1010. Sб. ц. = 4 × 5 = 20 (см2), […]...
- Рівнобедрений трикутник Геометрія Основні властивості найпростіших геометричних фігур Рівнобедрений трикутник Трикутник називається Рівнобедреним, якщо у нього дві сторони рівні. Ці сторони називаються Бічними сторонами, а третя сторона – Основою трикутника. На рисунку: ABC – рівнобедрений трикутник; – бічні сторони; AC – основа. Теорема 1. У рівнобедреному трикутнику кути при основі є рівними. Теорема 2. У рівнобедреному трикутнику […]...
- Об’єм кулі Геометрія Об’єми тіл Об’єм кулі На рисунку зображено кулю, кульовий сегмент і кульовий сектор. Об’єм кулі: , де R – радіус кулі. Об’єм кульового сегмента: , де H – висота кульового сегмента, R – радіус кулі. Об’єм кульового сектора: , де R – радіус кулі, H – висота відповідного кульового сегмента. Іноді треба знайти об’єм […]...
- Куля Геометрія Тіла обертання Куля Кулею називається тіло, що складається з усіх точок простору, які розташовані від даної точки на відстані, що не більша за дану. Ця точка називається Центром кулі, а дана відстань – Радіусом кулі. Межа кулі називається Кулевою поверхнею, або Сферою. Відрізок, що сполучає дві точки кульової поверхні й проходить через центр кулі, […]...
- Циліндр. Площа поверхні та об’єм циліндра УРОК № 56 Тема. Циліндр. Площа поверхні та об’єм циліндра Мета уроку: повторення, приведення в систему й розширення відомостей про циліндр, площу поверхні та об’єм циліндра; формування вмінь учнів знаходити площі поверхонь і об’єми циліндрів. Тип уроку: комбінований. Наочність і обладнання: таблиця “Початкові відомості стереометрії” [13]; моделі циліндрів. Вимоги до рівня підготовки учнів: пояснюють, що […]...
- Прямий круговий конус – СТЕРЕОМЕТРІЯ Формули й таблиці МАТЕМАТИКА СТЕРЕОМЕТРІЯ Прямий круговий конус...
- Циліндр 940. Нехай дано циліндр, ABCD – осьовий переріз циліндра, AO = r – радіус циліндра, AC = d – діагональ осьового перерізу: А) ΔABC — прямокутний. BC – висота циліндра; Б) SABCD – площа діагонального перерізу. В) Площа бічної поверхні: Г) Площа поверхні циліндра 941. Нехай дано циліндр, діагональ осьового перерізу циліндра дорівнює D і […]...
- Вписані кулі Геометрія Комбінації геометричних тіл Вписані кулі Якщо куля вписана в призму, то в її перпендикулярний переріз можна вписати коло. Висота призми дорівнює діаметру кола, вписаного в перпендикулярний переріз призми, тобто діаметру вписаної кулі. Центр кулі – середина висоти призми, що проходить через центр кола, яке вписане в перпендикулярний переріз. Центр кулі, яка вписана в пряму […]...
- Трапеція – ЧОТИРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ЧОТИРИКУТНИКИ Трапеція Щонайменше дві сторони паралельні, а дві інші – непаралельні Середня лінія трапеції – відрізок, що сполучає бічні сторони трапеції....
- Означення трапеції. Окремі види трапецій Урок № 13 Тема. Означення трапеції. Окремі види трапецій Мета: сформувати в учнів поняття трапеції, її елементів; розглянути означення рівнобічної та прямокутної трапецій, зміст властивостей кутів трапеції, прилеглих до бічної сторони, та кутів рівнобічної трапеції. Формувати вміння: – відтворювати вивчені твердження; – виконувати рисунок за описом; – за готовим рисунком знаходити елементи трапеції; – розв’язувати […]...
- Об’єм піраміди і конуса 1. Об’єм Піраміди Хеопса V дорівнює: 2. Знайдемо відношення довжин висоти і сторони основи на прикладі піраміди Хеопса. Площа основи піраміди – квадрат з площею 5,3 га. Отже, сторона основи дорівнює приблизно 230,22 м. Відношення стoрони основи до висоти: що приблизно дорівнює Співвідношенню золотого перерізу. З. Нехай висота n-кутної піраміди Н – 10 м. 1. […]...
- Окремі види трапецій та їх властивості Урок № 14 Тема. Окремі види трапецій та їх властивості Мета: доповнити знання учнів властивостями та ознаками окремих видів трапецій і домогтися засвоєння змісту вивчених тверджень; сформувати вміння відтворювати вивчені властивості та ознаки окремих видів трапецій, а також використовувати їх у здійсненні послідовних міркувань під час розв’язування задач. Тип уроку: застосування знань, умінь та навичок. […]...
- Тіла і поверхні обертання 905. На рисунку тіло, утворене обертанням прямокутника навколо його сторони. 906. А) Тіло, утворене обертанням прямокутного трикутника навколо катета, Б) Тіло, утворене обертанням прямокутного трикутника навколо гіпотенузи. ΔABC – прямокутний, AB – гіпотенуза. 907. Площина симетрії тіла обертання проходить через його вісь. 908. Див. рис. 909. У площині прямокутника ззовні його і паралельно одній з […]...
- Властивості призми 1. 2. 3. Ні, не можна. 4. Бічні ребра перпендикулярні до основи. Усі бічні грані – прямокутники. Бічне ребро є висотою призми. Площа бічної поверхні – добуток периметра Основи на довжину бічного ребра. 5. Так, може. Див. мал. до № 2. 6. 1) Основа правильної призми – правильний багатокутник, Усі бічні грані – рівні прямокутники. […]...