ЦИЛІНДР. КОНУС. КУЛЯ
Розділ 3 ВІДНОШEННЯ І ПРОПОРЦІЇ
§ 18. ЦИЛІНДР. КОНУС. КУЛЯ
У 5 класі ви вже ознайомилися з просторовими фігурами: прямокутним паралелепіпедом і кубом. ь на малюнок 56. Ви бачите предмети, які використовують у побуті. У сі вони мають одну й ту саму форму – циліндра (мал. 57).

Мал. 56
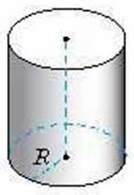
Мал. 57
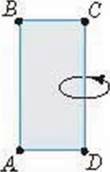
Мал. 58

Maл. 59
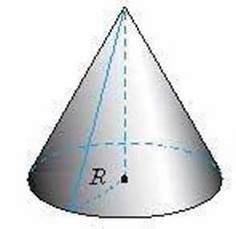
Мал. 60
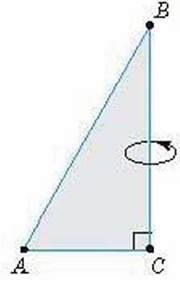
Мал. 61
Циліндр можна утворити, якщо обертати
Під час обертання твірна циліндра описує поверхню, яку називають бічною поверхнею циліндра. Повну поверхню циліндра утворюють його бічна поверхня і два круги основ.
На малюнку 59 ви бачите індіанське житло “типи”, яке має форму конуса (мал. 60).
Конус можна утворити, якщо обертати прямокутний трикутник ABC навколо однієї зі
Обертаючись, твірна конуса описує поверхню – бічну поверхню конуса” Повну поверхню конуса, утворюють його бічна поверхня і круг основи.
На малюнку 62 ви бачите предмети, що мають форму кулі (мал. 63).
Кулю можна утворити, якщо обертати круг навколо його діаметра АВ (мал. 64). Цей діаметр вважають віссю кулі. Радіус кулі R = OA і становить половину діаметра AB круга

Мал. 62
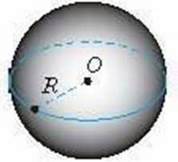
Мал. 63
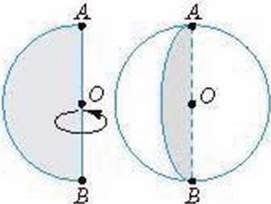
Мал. 64
Поверхня кулі ма спеціальну назву – сфера. Циліндр, конус і кулю отримано внаслідок обертання прямокутника, прямокутного трикутника та круга. Тому ці просторові фігури називають тілами обертання. Більш детально ви ознайомитеся з цими фігурами пізніше, у курсі геометрії.
Дізнайтеся більше
Для виготовлення моделі просторової фігури користуються її розгорткою.
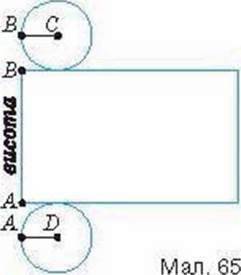
Щоб отримати розгортку циліндра (мал. 65), відокремлюють основу, а бічну поверхню розрізають уздовж твірної і розгортають на площині. Бічна поверхня циліндра розгортається у прямокутник, одна сторона якого дорівнює твірній, а друга – має довжину кола основи. Розгортка циліндра складається із цього прямокутника і двох кругів о снов.
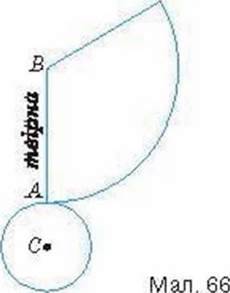
Щоб отримати розгортку конуса (мал. 66), відокремлюють основу, а бічну поверхню розрізають уздовж твірної ВА і розгортають на площині.
Бічна поверхня конуса розгортається в сектор. Розгортка конуса складається із цього сектора і круга основи конуса.
Для кулі виготовити традиційну розгортку неможливо.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Які фігури відносять до тіл обертання?
2. Поясніть, як утворюють циліндр.
3. Назвіть основні характеристики циліндра.
4. Поясніть, як утворюють конус,
5. Назвіть основні характеристики конуса.
6. Поясніть, як утворюють кулю.
7. Назвіть основні характеристики кулі.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
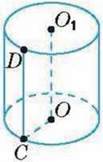
749′. За малюнком 67 назвіть:
1) вісь циліндра; 2) твірну циліндра;
3) висоту циліндра; 4) радіус основи циліндра.
750′. Чи дістанемо циліндр обертанням квадрата навколо його сторони?
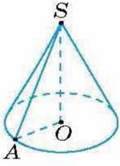
751′. За малюнком 68 назвіть:
1) вісь конуса; 2) твірну конуса;
3) висоту конуса; 4) радіус основи конуса.
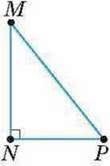
752′. На малюнку 69 зображено прямокутний трикутник MNP. Навколо яких сторін можна обертати трикутник MNP, щоб утворити конус?
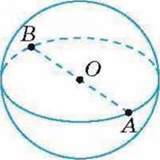
753′. За малюнком 70 назвіть: 1) вісь кулі; 2) радіус кулі.
754′. Чи правий Андрійко, стверджуючи, що кулю можна отримати обертанням кола?
755°. Твірна циліндра дорівнює 10 см. Чому дорівнює висота цього циліндра?
756°. Висота циліндра дорівнює 8 см. Яка довжина твірної цього циліндра?
757°. Перемалюйте в зошит малюнок 71 і домалюйте зображення циліндра. Позначте на малюнку вісь, твірну і радіус нижньої основи циліндра.
Мал. 67
Мал. 68
Мал. 69
Мал. 70
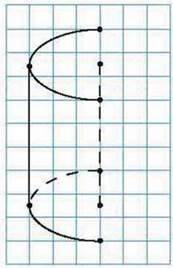
Мал. 71
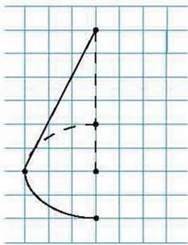
Мал. 72
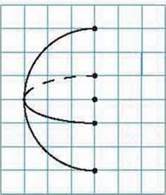
Мал. 73
758°. Схематично намалюйте циліндр. Позначте на малюнку вісь, твірну і радіус верхньої основи циліндра.
759°. Перемалюйте в зошит малюнок 72 і домалюйте зображення конуса. Позначте на малюнку вісь, твірну і радіус основи конуса.
760°. Схематично намалюйте конус. Позначте на малюнку вісь, твірну і радіус основи конуса.
761°. Перемалюйте в зошит малюнок 73 та домалюйте зображення кулі. Позначте на малюнку радіус ОА кулі.
762°. Схематично намалюйте кулю. Позначте на малюнку радіус ОВ кулі.
763. Чи завжди рівні циліндри, у яких рівні:
1) радіуси основ; 2) висоти; 3) твірні?
764. У циліндрі довжини радіуса основи і висоти відносяться, як 2 : 5. Знайдіть, чому дорівнюють радіус основи і висота цього циліндра, якщо висота на 3 см більша за радіус основи.
765. У циліндрі довжини радіуса основи і твірної відносяться, як 4 : 6. Знайдіть, чому дорівнюють радіус основи і висота цього циліндра, якщо радіус основи на 8 см менший від твірної.
766. Чи завжди рівні конуси, у яких рівні:
1) радіуси основ; 2) висоти; 3) твірні?
767. У конусі довжини висоти і радіуса основи відносяться, як 7 : 3. Знайдіть, чому дорівнюють радіус основи і висота цього конуса, якщо радіус основи на 4 см менший від висоти.
768. У конусі довжини твірної і радіуса основи відносяться, як 5 : 2. Знайдіть, чому дорівнюють радіус основи і твірна цього конуса, якщо твірна на 6 см більша за радіус основи.
769. Чи завжди рівні кулі, у яких рівні: 1) радіуси; 2) діаметри?
770. Дано дві кулі, радіуси яких відносяться, як 2 : 3. Знайдіть радіус більшої кулі, якщо радіус меншої дорівнює 5 см.
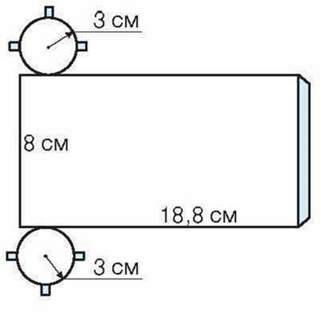
Мал. 74
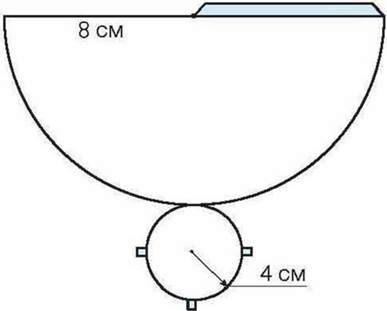
Мал. 75
771. Дано дві кулі, радіуси яких відносяться, як 8 : 5. Знайдіть радіус меншої кулі, якщо радіус більшої дорівнює 12 см.
772*. Площа основи циліндра дорівнює 12,56 см2. Знайдіть твірну циліндра, якщо його висота на 5 см більша за радіус основи.
773*. Довжина кола основи конуса дорівнює 37,68 см. Знайдіть висоту і твірну конуса, якщо радіус основи, висота і твірна конуса відносяться, як 3 : 4 : 5.
774*. Діаметр земної кулі приблизно дорівнює 12,7 тис. км. Знайдіть радіус Землі та довжину екватора.
775*. Земну кулю стягнули обручем уздовж екватора. Потім збільшили довжину обруча на 1 м. Чи зможе кіт пролізти в утворену щілину?
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
776. Наведіть приклади предметів довкілля, які мають форму:
1) циліндра; 2) конуса; 3) кулі.
777. Зробіть моделі циліндра і конуса за допомогою креслення розгорток на малюнках 74 і 75.
ЗАДАЧІ НА ПОВТОРЕННЯ
778. Розв’яжіть рівняння:
1) 25-24 : (х+ 12,2) = 24,4;
2)(х + 12):0,25+ 16= 166.
779. Сергійко купив 6 зошитів у клітинку по 4,5 грн за штуку і 8 зошитів у лінійку по 4 грн за штуку. Скільки грошей залишилось у Сергійка, якщо мама дала йому 80 грн?
