Головна ⇒ 📌Довідник з математики ⇒ Арифметична прогресія
Арифметична прогресія
Математика – Алгебра
Послідовності
Арифметична прогресія
Арифметичною прогресією називається послідовність, кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додають одне й те саме число. Це стале для даної послідовності число d називається Різницею арифметичної прогресії.
Арифметична прогресія буде зростаючою, якщо 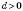 , і спадною, якщо
, і спадною, якщо 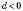 .
.
Прогресію можна задати за допомогою першого члена 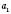 і різниці прогресії
і різниці прогресії
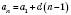 .
.Теорема 1. Будь-яка арифметична прогресія може бути задана формулою виду
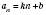 , де k і b – деякі числа, і навпаки, послідовність, яка задана формулою виду
, де k і b – деякі числа, і навпаки, послідовність, яка задана формулою виду 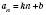 , де k і b – деякі числа, є арифметичною прогресією.
, де k і b – деякі числа, є арифметичною прогресією.Теорема 2. Послідовність тоді й тільки тоді є арифметичною прогресією, якщо кожний її член, починаючи з другого, є середнім арифметичним двох сусідніх:
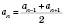 (*)
(*)Формула суми перших n членів арифметичної прогресії:
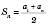 або
або 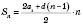 .
.Related posts:
- Арифметична прогресія. Формула n-го члена арифметичної прогресії УРОК № 51 Тема. Арифметична прогресія. Формула n – го члена арифметичної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять арифметичної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена арифметичної прогресії. Закріпити вміння: вирізняти арифметичну прогресію серед числових послідовностей, відшукувати різницю арифметичної прогресії, перші члени […]...
- Властивості прогресій – ПРОГРЕСІЇ Формули й таблиці МАТЕМАТИКА ПРОГРЕСІЇ Нескінченною числовою послідовністю називається числова функція, визначена на множині натуральних чисел: Арифметична прогресія Геометрична прогресія Арифметичною прогресією називається така послідовність чисел, при якій кожен член, починаючи із другого, дорівнює попередньому, доданому до одного й того самого, постійного для цього ряду числа. Геометричною прогресією називається така послідовність чисел, при якій кожен […]...
- Геометрична прогресія Математика – Алгебра Послідовності Геометрична прогресія Геометричною прогресією називається послідовність відмінних від 0 чисел, кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те саме число. Це стале для даної послідовності число q називають Знаменником геометричної прогресії. Формула n-го члена геометричної прогресії: . Теорема. Послідовність тоді й тільки тоді є геометричною […]...
- Геометрична прогресія УРОК № 54 Тема. Геометрична прогресія Мета уроку: домогтися засвоєння учнями: означення геометричної прогресії, відповідної термінології (знаменник геометричної прогресії), її рекурентної формули та основних властивостей геометричної прогресії (включаючи характеристичну властивість). Виробити вміння: відтворювати зміст вивчених понять, а також використовувати їх для розв’язування задач, що передбачають виділення геометричної прогресії серед інших числових послідовностей, використання рекурентної формули […]...
- Геометрична прогресія. Формула n-го члена геометричної прогресії УРОК № 55 Тема. Геометрична прогресія. Формула n-го члена геометричної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед інших числових послідовностей, відшукувати знаменник геометричної прогресії, перші кілька членів […]...
- Числові послідовності УРОК № 65 Тема. Числові послідовності Тестові завдання 1. Послідовність задано формулою аn = 5n + 2. Знайдіть а3. А) 3; б) 17; в) 5; г) інша відповідь. 2. В арифметичній прогресії (bп) різниця дорівнює 2. Знайдіть b10, якщо b1 = 3. А) 1536; б) 18; в) 21; г) інша відповідь. 3. Знайдіть суму перших […]...
- Сума перших n членів арифметичної прогресії УРОК № 53 Тема. Сума перших n членів арифметичної прогресії Мета уроку: закріпити знання учнів про формули обчислення суми перших n членів арифметичної прогресії, а також про її означення та властивості, вивчені на попередніх уроках; сформувати уявлення про спосіб розв’язування задач на відшукання суми послідовних членів арифметичної прогресії з n-го по т-й включно (n < […]...
- Сума перших n членів геометричної прогресії УРОК № 57 Тема. Сума перших n членів геометричної прогресії Мета уроку: закріпити знання учнів про зміст означення та супутніх понять геометричної прогресії, а також про її основні властивості. Доповнити ці знання знанням формули n-го члена геометричної прогресії. Закріпити вміння: вирізняти геометричну прогресію серед числових послідовностей, відшукувати знаменник геометричної прогресії, перші члени геометричної прогресії, а […]...
- Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю . . Теорема 2. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю, яка дорівнює ab: . Наслідки 1) Сталий множник можна виносити за знак границі. […]...
- Властивості нескінченно малих послідовностей Математика – Алгебра Границя Властивості нескінченно малих послідовностей Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю. Послідовність називається Обмеженою, якщо існує таке число , що для всіх значень 2, … виконується нерівність . Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою послідовністю. Послідовність називається Нескінченно […]...
- Послідовності Математика – Алгебра Послідовності Розглянемо яку-небудь множину, що містить дійсних чисел і кожний елемент якої відповідає одному з натуральних чисел від 1 до , або нескінченну множину дійсних чисел, кожному елементу якої можна поставити у відповідність натуральне число. Такі числа можна записати в певному порядку. Кажуть, що вони утворюють Послідовність. Наприклад: 2; 4; 6; 8; […]...
- Границя числової послідовності Математика – Алгебра Границя Границя числової послідовності Число a називається Границею послідовності,, …, , …, якщо для будь-якого додатного числа існує таке натуральне число , що для всіх виконується нерівність . Позначеня: , або . Послідовність , , 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що […]...
- Множення вектора на число Геометрія Вектори Множення вектора на число Добутком вектораНа число називається вектор , тобто . Для будь-якого вектора і чисел і . Для будь-яких двох векторів і і числа . Теорема 1. Абсолютна величина вектора дорівнює . Напрям вектора , якщо , збігається з напрямом вектора , якщо , і протилежний напряму вектора , якщо . […]...
- Властивості пропорції – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Відношення числа а до числа b – дріб a/b. Пропорція – рівність двох відношень: a/b = c/d. Основна властивість пропорції Якщо a/b = c/d правильно, то ad = bc. Властивості пропорції А) a/b = c/d правильна → a/c = b/d правильна; Б) a/b = c/d правильна → d/b = […]...
- Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Числові послідовності. Властивості числових послідовностей УРОК № 49 Тема. Числові послідовності. Властивості числових послідовностей Мета уроку: домогтися засвоєння учнями змісту понять: числова послідовність, n-й член числової послідовності, формула п-го члена; списку способів задання числової послідовності. Виробити вміння: відтворювати вивчені означення; знаходити члени послідовності із заданими номерами, якщо послідовності задані різними способами. Повторити означення числової функції, а також супутні поняття. Тип […]...
- Ромб Геометрія Чотирикутники Ромб Ромб – це паралелограм, у якого всі сторони рівні. Властивості ромба Оскільки ромб є паралелограмом, він має всі властивості паралелограма і деякі інші. Теорема 1. Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів. На рисунку ABCD – ромб; ; ; ; ; . Теорема 2. Діагоналі ромба розбивають […]...
- Степінь з раціональним показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь з раціональним показником N ) Для будь-якого невід’ємного числа а й натурального числа n (n ≥ 2) існує одне невід’ємне число b, при якому bn = а й позначається . Звідси випливає: 1. = 0 тільки при а = 0; 2. = 1 тільки при а = […]...
- Дії з комплексними числами – КОМПЛЕКСНІ ЧИСЛА Формули й таблиці МАТЕМАТИКА КОМПЛЕКСНІ ЧИСЛА Числа виду а + ib, де а і b – будь-які дійсні числа, і – уявна одиниця, називаються комплексними. І2 = -1 – уявна одиниця. Z = a + ib. ReZ = a – дійсна частина числа Z. LmZ = ib – уявна частина числа Z. B – коефіцієнт […]...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Пропорційність відрізків хорд і січних кола Геометрія Кути, пов’язані з колом Пропорційність відрізків хорд і січних кола Теорема 1. Якщо хорди AB і CD кола перетинаються в точці S, то (рисунок 1). Теорема 2. Якщо з точки P до кола проведені дві січні, що перетинають коло відповідно в точках A, B, C, D, то (рисунок 2). Тобто добуток січної, проведеної до […]...
- Теорема Вієта Математика – Алгебра Квадратні корені Теорема Вієта Теорема 1 (Вієта). Якщо незведене квадратне рівняння має два корені, то , . Якщо зведене квадратне рівняння має два корені, то ; . Коли рівняння має один корінь, його можна вважати за два рівних: . Тоді для незведеного квадратного рівняння ; ; для зведеного , . Зверніть увагу: […]...
- Прямокутник Геометрія Чотирикутники Прямокутник Прямокутник – це паралелограм, у якого всі кути прямі. Властивості прямокутника Оскільки прямокутник є паралелограмом, він має всі властивості паралелограма і ще деякі інші. Теорема. Діагоналі прямокутника рівні. На рисунку . . ; – рівнобедрені. Ознаки прямокутника Теорема 1. Якщо в чотирикутнику всі кути рівні, то він є прямокутником. Теорема 2. Якщо […]...
- Подільність цілих чисел Формули й таблиці МАТЕМАТИКА Подільність цілих чисел Ціле число а ділить ціле число b, або b ділиться на а, якщо існує таке ціле число с, при якому b = ас. Це має місце тоді, коли остача від ділення числа b на число а дорівнює нулю. Подільність цілих чисел має такі властивості: 1. Будь-яке ціле число […]...
- Повторення (цикл). Алгоритм з повторенням Розділ 3. АЛГОРИТМИ З ПОВТОРЕННЯМ ТА РОЗГАЛУЖЕННЯМ 3.1. Повторення (цикл). Алгоритм з повторенням Запитання для повторення вивченого 1. Алгоритм – це скінченна послідовність команд, виконання яких приводить до розв’язання поставленої задачі. Збір учня до школи. Перехід дорогу з світлофором та без нього. 2. Дощ, снігопад, блискавка, грім. 3. Виконавець алгоритму може не мати уявлення про […]...
- Додатні та від’ємні числа Математика – Алгебра Раціональні числа Додатні та від’ємні числа Координатна пряма Пряма з вибраними на ній початком відліку, одиничним відрізком і вказаним додатним напрямом називається Координатною прямою. Число, що показує положення точки на координатній прямій, називається Координатою точки. Приклад Точка А розташована на прямій (див. рисунок) на відстані 2,5 одиничних відрізка праворуч від 0. Це […]...
- Прості й складені числа Математика – Алгебра Подільність натуральних чисел Прості й складені числа Натуральне число називається Простим, якщо воно має тільки два різних дільники: одиницю й саме це число. Число, яке має більше двох дільників, називається складеним. Число 1 має єдиний дільник – 1, тому не належить ні до простих, ні до складених чисел. Приклади 1) Числа 2, […]...
- Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...
- Формули косокутних трикутників 10. Додатки 36. Формули косокутних трикутників Теорема синусів: Теорема косинусів: Теорема тангенсів:...