Головна ⇒ 📌Довідник з математики ⇒ Арифметичні операції над диференційовними функціями
Арифметичні операції над диференційовними функціями
Математика – Алгебра
Похідна
Арифметичні операції над диференційовними функціями
Теорема 1. Якщо функції 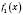 і
і 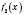 в точці
в точці 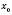 мають похідні, то функція
мають похідні, то функція 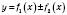 в цій точці також має похідну, яка дорівнює
в цій точці також має похідну, яка дорівнює
.
Теорема 2. Якщо функції 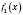 і
і 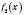 в точці
в точці 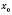 мають похідні, то в цій точці функція
мають похідні, то в цій точці функція 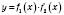 також має похідну, яка дорівнює
також має похідну, яка дорівнює
.
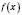 має похідну в точці
має похідну в точці 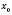 , то функція
, то функція 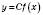 також має похідну в цій точці, яка дорівнює
також має похідну в цій точці, яка дорівнює 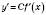 .
.Теорема 3. Якщо функції
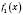 і
і 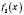 в точці
в точці 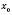 мають похідні й
мають похідні й 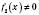 , то функція
, то функція 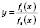 також має похідну в точці x:
також має похідну в точці x: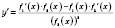 .
.Нехай функція f ставить у відповідність числу x число y, а функція g – числу y число z. Тоді функцію h, яка ставить у відповідність числу x
Позначення:
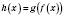 .
.Зверніть увагу: область визначення функції
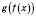 – це множина таких значень x з області визначення функції f, для яких
– це множина таких значень x з області визначення функції f, для яких 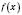 належить області визначення функції g.
належить області визначення функції g.Теорема 4. Якщо функція f має похідну в точці
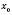 , а функція g має похідну в точці
, а функція g має похідну в точці 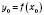 , то складена функція
, то складена функція 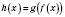 також має похідну в точці
також має похідну в точці 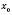 , причому
, причому 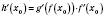 .
.Нехай функція f має похідну
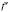 в усіх точках проміжку
в усіх точках проміжку 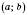 . Ця похідна, у свою чергу, є функцією від x. Якщо функція
. Ця похідна, у свою чергу, є функцією від x. Якщо функція 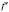 діференційовна, то її похідну називають Другою похідноюF і позначають
діференційовна, то її похідну називають Другою похідноюF і позначають 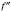 .
.Таким чином,
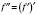 .
.Таким же чином дають означення похідної n-го порядку
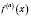 .
.Related posts:
- Правила диференціювання – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила диференціювання Правило 1. Якщо функції у = f(x) і у = g(x) мають похідну в точці х, то і їх сума має похідну в точці х, до того ж похідна суми дорівнює сумі похідних: Правило 2. Якщо функція у = f(x) має похідну в точці х, то і […]...
- Застосування похідної Математика – Алгебра Похідна Застосування похідної Нехай функція визначена на проміжку і . Функція називається Зростаючою в точці, якщо існує інтервал , де , який міститься у проміжку і є таким, що для всіх x з інтервалу і для всіх x з інтервалу . Функція називається Спадною в точці, якщо існує інтервал , який міститься […]...
- Похідна Математика – Алгебра Похідна Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує до нуля, тобто . Функція в точці називається Диференційовною, якщо в цій точці вона має похідну . Якщо функція є диференційовною в кожній точці деякого інтервалу , то вона називається […]...
- Основні теореми про границі функцій Математика – Алгебра Границя Основні теореми про границі функцій Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому ; . Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює . […]...
- Границя функції Математика – Алгебра Границя Границя функції Нехай функція визначена на проміжку (можливо, що ). Число A називається границею функції у точці , якщо для будь-якого числа існує таке число , що для всіх , і таких, що , виконується нерівність . Позначення: , або . Нехай – внутрішня точка проміжку . Функція називається нескінченно малою […]...
- Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
- Неперервність функції в точці Математика – Алгебра Границя Неперервність функції в точці Нехай функція визначена на проміжку і точка є внутрішньою точкою цього проміжку. Функція називається Неперервною в точці, якщо існує границя функції в цій точці й вона дорівнює значенню функції в точці . Нехай функція визначена в усіх точках деякого проміжку . Візьмемо дві довільні точки з цього […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
- Поняття первісної функції – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Поняття первісної функції Первісною для даної функції на заданому проміжку називається така функція , що для всіх . Операція знаходження первісної F для даної функції називається Інтегруванням. Теорема 1. Будь-яка неперервна на відрізку функція має первісну функцію. Лема. Якщо на деякому проміжку, то на цьому проміжку, де C […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Основні теореми про границі числової послідовності Математика – Алгебра Границя Основні теореми про границі числової послідовності Теорема 1. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю . . Теорема 2. Нехай послідовності і мають відповідно границі a і b. Тоді послідовність має границю, яка дорівнює ab: . Наслідки 1) Сталий множник можна виносити за знак границі. […]...
- Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Первісна функція Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х (а;b), що дорівнює f(x): F'(x) = f(x). Загальний вигляд первісної F(x) + C, де С – довільне стале число. Теорема. Будь-яка неперервна на функція y = f(x) […]...
- Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...
- Поняття про обернену функцію Математика – Алгебра Тригонометричні функції Поняття про обернену функцію Функція, яка приймає кожне своє значення в єдиній точці області визначення, є Оборотною. У такої функції за значенням залежної змінної можна однозначно визначити, якому значенню аргументу воно відповідає. Інакше кажучи, якщо функція є оборотною й число а належить до її області значень , то рівняння має […]...
- Способи задання функції 789. 1) Аргумент t, залежна змінна s; 2) аргумент x, залежна змінна у; 3) аргумент а, залежна змінна V; 4) аргумент x, залежна змінна f. 790. у = 10x + 1 1) Якщо x = -1, то у = 10 • (-1) + 1 = -9. 2) Якщо x = 3, то у = 10 […]...
- Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Похідна функція – визначення похідної функції. Рівняння дотичної до графіка функції y = f(x) у точці М(х0,у0): – кутовий коефіцієнт дотичної....
- Правила знаходження первісних – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила знаходження первісних Правило 1. Якщо функції у = f(x) і у = g(x) мають на числовому проміжку X первісні, відповідно у = F(x) й у = G(x), то і сума функцій у = f(x) + g(x) має на проміжку X первісну у= =F(x) + G(x). (Первісна суми дорівнює […]...
- Вправи для повторення розділу 2 До § 19. 819. Площа квадрата залежить від довжини його сторони. Площа квадрата є функцією від довжини сторони квадрата: S = х2. Якщо сторона квадрата а, то площа S = а2. 820. X -4 -2 0 2 4 Y 2/7 0 -2/3 -4 6 G 8/5 -6/5 -4/5 -2/5 0 821. у = 48 – […]...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- Арифметичні дії додавання і віднімання, множення і ділення Арифметичні дії додавання і віднімання, множення і ділення Властивості та закони арифметичних дій 1 Перевір розв’язання. Які закони або властивості застосовано для обчислень? 43 + 29 = 43 + (20 + 9) = (43 + 20) + 9 = 63 + 9 = 72 43 + 29 = 43 + (7 + 22) = (43 […]...
- Узагальнення поняття степеня Математика – Алгебра Степенева функція Узагальнення поняття степеня Основнi означення 1. Якщо n Є N, , то , де a – довільне число. 2. , де а – довільне число. 3. для . не має змісту. 4. , n Є N, . 5. , n Є N, m Є Z, . Властивості степеня з раціональним […]...
- Лабораторна робота № 3. Внутрішня будова кореня у зв’язку з його функціями Розділ І. РОСЛИНИ Тема 1. Будова та життєдіяльність рослин (на прикладі покрито-насінної дводольної рослини) УРОК 8 * Тема. Лабораторна робота № 3. Внутрішня будова кореня у зв’язку з його функціями Мета. Розширити знання учнів про анатомічну будову кореня у зв’язку із функціями, що вони виконують. Основні поняття і терміни: кореневий чохлик, зона ділення, зона росту, […]...
- Арифметичні дії з круглими числами Мета: формування поняття про багатоцифрові числа. Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати спосіб міркування стосовно визначення загальної кількості одиниць певного розряду в багатоцифровому числі. Актуалізувати вміння визначати розрядні одиниці; замінювати числа більшими розрядними одиницями. Актуалізувати прийом укрупнення розрядних одиниць при додаванні, відніманні, множенні та діленні трицифрових чисел; перенести цей спосіб міркування на дії з […]...
- Завдання для перевірки знань до §§ 19-21 1. 1) у = х2 + х; 3) – функції. 2. 1) у = 3х – 7; 3) у = 4 – лінійні функції. 3. 1) у = -2х + 6; k = -2; l = 6; 2) у = 7,4x; k = 7,4; l = 0. 4. у = -2х + 7; 1) х […]...
- Арифметичні дії додавання і віднімання Метою розділу є формування в учнів навичок письмового додавання та віднімання багатоцифрових чисел. Слід зазначити, що з письмовим прийомами додавання та віднімання учні ознайомились у 3-му класі, на початку навчального року в 4-му класі алгоритми письмових прийомів були актуалізовані, водночас розглядалось письмове додавання у випадку трьох доданків. Таким чином, тривалий час було відведено для формування […]...
- Нерівності Математика – Алгебра Нерівності Число а вважається більшим від b, якщо різниця – число додатне. Число a менше від b, якщо різниця – число від’ємне. Якщо , то числа a і b рівні. На координатній прямій меншому числу відповідає точка, що лежить ліворуч від точки, яка відповідає більшому числу. Позначення: – a менше від b; […]...
- Зростаючі й спадні функції Математика – Алгебра Числові функції Зростаючі й спадні функції Функція називається Зростаючою на деякому інтервалі, якщо для будь-яких двох значень аргументу з цього інтервалу більшому значенню аргументу відповідає більше значення функції. Функція називається Спадною На деякому інтервалі, якщо для будь-яких значень аргументу з цього інтервалу більшому значенню аргументу відповідає менше значення функції. Приклади 1) y […]...
- Екстремуми функції Математика – Алгебра Числові функції Екстремуми функції Точку x0 називають Точкою мінімуму функції, а саме число – Мінімумом функції, якщо існує інтервал , , на якому функція визначена і для всіх із цього інтервалу. Точку називають Точкою максимуму функції, а саме число – Максимумом функції, якщо існує інтервал , , на якому функція визначена і […]...
- Співвідношення між тригонометричними функціями одного аргументу УРОК 12 Тема. Співвідношення між тригонометричними функціями одного аргументу Мета уроку: вивчення співвідношення між тригонометричними функціями одного аргументу, формування умінь застосовувати вивчені співвідношення для тотожних перетворень (спрощення) виразів, знаходження значень тригонометричних функцій за однією відомою функцією. І. Аналіз контрольної роботи II. Мотивація навчання Дуже часто при розв’язуванні задач виникає проблема: знайти значення тригонометричних функцій, якщо […]...