Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Багаточлен. Дії з багаточленами

Багаточлен. Дії з багаточленами

Урок № 42

Тема. Б агаточлен. Дії з багаточленами

Мета: контроль засвоєння знань та вмінь з перетворення суми, різниці, добутку багаточленів у багаточлен стандартного вигляду та розв’язування задач, пов’язаних із цими вміннями.

Тип уроку: контроль засвоєння знань та вмінь.

Хід уроку

І. Умова тематичної контрольної роботи

Варіант 1

Варіант 2

№ 1. Перетворіть вираз у багаточлен:

№ 1. Перетворіть вираз у багаточлен:

1) (5х2 + 6х – 3)

– (2х2 – 3х – 4);

1) (7х2 – 4х + 8) – (4х2 + х – 5);

2) 3х(х3 – 4х + 6);

2) -5а(а4 – 6а2 + 3);

3) (х + 3)(2х – 1).

3) (х + 4)(3х – 2).

№ 2. Розкладіть на множники:

№ 2. Розкладіть на множники:

1) 5а2 – 20ab;

1) 18ху – 6х2;

2) 7х3 – 14х5 + 21х2;

2) 15а6 – 3а4 + 9а2;

3) 3а – 3b + ах – bх.

3) 4х – 4у + сх – су.

№ 3. Спростіть вираз та обчисліть його значення:

№ 3. Спростіть вираз та обчисліть його значення:

4m(3 + 5m) – (m + 1)(m – 2)

7b(2b + 3) – (b + 6)(b

– 5)

При m = -0,2.

При b = -0,1.

№ 4. Розв’яжіть рівняння:

№ 4. Розв’яжіть рівняння:

1) 4х2 – 12х = 0;

1) 3х2 + 9х = 0;

2) х(х – 2) + 5(х – 2) = 0;

2) х(х – 4) + 7(х – 4) = 0;

3) (2х – 3)(х + 7) = (х – 4)(2х + 3) + 3.

3) (3х + 4)(4х – 3) – 3х = (2х + 5)(6х – 7).

№ 5. Доведіть, що вираз 165 – 86 ділиться на 3.

№ 5. Доведіть, що вираз 274 – 95 ділиться на 8.

№ 6. Знайдіть 4 послідовних натуральних числа, якщо відомо, що добуток

Третього та четвертого чисел більший від добутку першого та другого на 34.

№ 6. Знайдіть 4 послідовних натуральних числа, якщо відомо, що добуток

Другого та четвертого чисел більше за добуток першого і третього на 31.

№ 7. Додатково. Розв’яжіть рівняння х2 + 8х + 15 = 0

№ 7. Додатково. Розв’яжіть рівняння х2 + 7х + 12 = 0

II. Розв’язування завдань тематичної контрольної роботи

Варіант 1

Варіант 2

№ 1. 1) 5х2 + 6х – 3 – 2х2 + 3х + 4 = 3х2 + 9х + 1;

№ 1. 1) 7х2 – 4х + 8 – 4х2 – х + 5 = 3х2 – 5х + 13;

2) 3х4 – 12х2 + 18х;

2) -5а5 + 30а3 – 15а;

3) 2х2 + 5х – 3.

3) 3х2 + 10х – 8.

№2. 1) 5а(а – 4b);

№2. 1) 6х(3у – х);

2) 7х2(х – 2х3 + 3);

2) 3а2(5а4 – а2 + 3);

3) 3(а – b) + х(а – b) = (а – b)(1 + х).

3) 4(х – у) + с(х – у) = (х – у)(4 + с).

№ 3. 12т + 20т2 – т2 + т + 2 =

= 19т2 + 13т + 2.

№3. 14b2 + 21b – b2 – b + 30 =

= 13b2 + 20b + 30.

Якщо т = -0,2, то

Якщо b = -0,1, то

19 • (-0,2)2 + 13 • (-0,2) + 2 = 19 • 0,04 – 2,6 + 2 = 0,76 – 2,6 + 2 = 2,76 – 2,6 = 0,16.

13 • (-0,1)2 + 20 • (-0,1) + 30 = 0,13 – 2 + 30 = 30,13 – 2 = 28,13.

№4.1) 4х(х – 3) = 0, х = 0 або х – 3 = 0, х = 3.

№4. 1) 3х(х + 3) = 0, х = 0 або х + 3 = 0, х = 0 або х = -3.

Відповідь. 0; 3.

Відповідь. -3; 0.

2) (х – 2)(х + 5) = 0,

2) (х – 4)(х + 7) = 0,

Х – 2 = 0 або х + 5 = 0,

Х – 4 = 0 або х + 7 = 0,

Х = 2 або х = -5.

Х = 4 або х = -7.

Відповідь. 2; -5.

Відповідь. -7; 4.

3) 2х2 + 11х – 21 = 2х2 – 5х – 12 + 3;

3) 12х2 + 7х – 12 – 36 = 12х2 + 16х – 35;

16х = 21 – 9; 16х = 12; Багаточлен. Дії з багаточленами; Багаточлен. Дії з багаточленами.

-9х = 13; Багаточлен. Дії з багаточленами; Багаточлен. Дії з багаточленами.

Відповідь. Багаточлен. Дії з багаточленами.

Відповідь. Багаточлен. Дії з багаточленами.

№5. 165 – 86 = (24)5 – (23)6 = 220 – 218 = 218(22 – 1) = 218 • 3

Ділиться на 3, бо один з множників 3.

№ 5. 274 – 95 = (33)4 – (32)5 = 312 – 310 = 310(32 – 1) = 310 • 8

Ділиться на 8, бо один з множників 8.

№ 6. Нехай менше число х, тоді наступні натуральні числа: 2-ге –

(х + 1); 3-тє – (х + 2); 4-те – (х + 3). За умовою задачі складаємо рівняння:

№ 6. Нехай найменше з поданих натуральних чисел х, тоді наступні за ним

Числа (х + 1), (х + 2), (х + 3). За умовою задачі складемо рівняння:

(х + 3)(х + 2) – х(х + 1) = 34,

(х + 3)(х + 1) – х(х + 2) = 31,

Х2 + 5х + 6 – х2 – х = 34,

Х2 + 4х + 3 – х2 – 2х = 31,

4х = 28, х = 7.

Х = 28.

Отже, шукані числа: 7, 8, 9, 10.

Отже, шукані числа: 28, 29, 30, 31.

Відповідь. 7, 8, 9, 10.

Відповідь. 28, 29, 30, 31.

№7. х2 + 8х + 15 = 0,

№7. х2 + 7х + 12 = 0,

Х2 + 3х + 5х + 15 = 0,

Х2 + 3х + 4х + 12 = 0,

Х(х + 3) + 5(х + 3) = 0,

Х(х + 3) + 4(х + 3) = 0,

(х + 3)(х + 5) = 0,

(х + 3)(х + 4) = 0,

Х = -3 або х = -5.

Х + 3 = 0 або х + 4 = 0,

Відповідь. -3; -5

Тоді х = -3 або х = -4.

Відповідь. -3; -4

ІІІ. Підсумки уроку

Самоперевірка (за готовими розв’язаннями), учні самостійно встановлюють теми для корекції.

IV. Домашнє завдання

1) Проаналізувавши помилки, виконати корекцію – умови контрольної роботи видано додому.

2) Випереджальне домашнє завдання. Перетворивши степінь на добуток, виконайте перетворення у багаточлен стандартного вигляду:

1) (a + b)2;(a + c)2; (a + d)2; (b + d)2;

2) (a – b)2; (a – c)2; (a – d)2; (b – d)2.

Порівняйте результати, зробіть висновки.


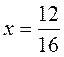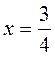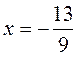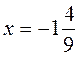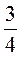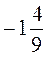1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Множення одночлена на багаточлен Урок № 34 Тема. Множення одночлена на багаточлен Мета: спираючись на знання розподільної властивості множення, сформулювати загальний алгоритм множення одночлена на багаточлен; виробити вміння застосовувати сформульоване правило (алгоритм) для перетворення добутку одночлена у багаточлен стандартного вигляду; вдосконалити вміння перетворювати багаточлени. Тип уроку: засвоєння знань, умінь та навичок. Хід уроку I. Перевірка домашнього завдання Перевірку домашнього […]...

  2. Багаточлен. Подібні члени багаточлена та їх зведення Урок № 31 Тема. Багаточлен. Подібні члени багаточлена та їх зведення Мета: домогтися свідомого сприйняття учнями змісту понять “багаточлен”, “подібні члени багаточлен”, “багаточлен стандартного вигляду”, “степінь багаточлена” та вдосконалити вміння зводити подібні доданки (подібні члени багаточлена). Тип уроку: засвоєння знань, формування вмінь. Хід уроку І. Організаційний етап. Аналіз тематичної контрольної роботи @ Оскільки за браком […]...

  3. Поняття рівняння. Розв’язування рівнянь 770. а) 5х = 3х + 4. Х = 2 – корінь рівняння, бo 5 • 2 = 3 • 2 + 4 – правильна рівність. Б) 2х + 8 = 7х. Х = 2 – не є коренем рівняння, 2 • 2 + 8 = 7 • 2 – неправильна рівність. В) 10 – […]...

  4. Урок узагальнення та систематизації знань з теми “Багаточлени” Урок № 41 Тема. Урок узагальнення та систематизації знань з теми “Багаточлени” Мета: повторити, узагальнити та систематизувати знання та вміння учнів, які вони дістали з теми “Багаточлени”. Тип уроку: систематизація та узагальнення знань. Хід уроку I. Перевірка домашнього завдання @ Для перевірки домашнього завдання вчитель збирає зошити, але оскільки аналіз самостійної роботи необхідний (тим більше, […]...

  5. Множення двох многочленів Урок № 35 Тема. Множення двох многочленів Мета: сформувати в учнів знання алгоритму множення двох багаточленів як наслідку з алгоритму множення одночлена на багаточлен; виробити вміння перетворювати добуток двох багаточленів у багаточлен стандартного вигляду за названим алгоритмом. Тип уроку: засвоєння знань. Хід уроку I. Перевірка домашнього завдання @ Обов’язково перевіряємо № 2, бо в ньому […]...

  6. Множення двох багаточленів Урок № 36 Тема. Множення двох багаточленів Мета: продовжувати формувати навички: 1) виконання дії множення двох багаточленів та перетворення цього добутку в багаточлен стандартного вигляду; 2) використання названого алгоритму в комплексі з іншими перетвореннями багаточленів, вивчених раніше. Тип уроку: засвоєння вмінь та навичок. Хід уроку І. Перевірка домашнього завдання @ Оскільки від того, чи засвоїли […]...

  7. ВСТУП ДО АЛГЕБРИ 8. 1) Якщо х = 4, то 2х – 3 = 2 • 4 – 3 = 8 – 3 = 5. Якщо х = 0, то 2х – 3 = 2 • 0 – 3 = 0 – 3 = -3. Якщо х = -3, то 2х – 3 = 2 • (-3) – […]...

  8. Лінійні рівняння з однією змінною 793. Лінійними рівняннями є рівняння: а) 2/9х = 8; в) -2,7y = 0. 794. а) 56х = 64; рівняння має 1 корінь, Б) 0х = -2; рівняння не має коренів; В) 8х = 0; рівняння має 1 корінь, х = 0; Г) 0у = 0; рівняння має безліч коренів. 795. а) 6х = 42; х […]...

  9. Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...

  10. Рівняння. Нерівності зі змінною Рівняння. Нерівності зі змінною 1 Розбий записи на дві групи. Назви кожну групу. 27 + х = 51 27 + х < 51 40 ∙ р > 160 2 Згадай, що ти знаєш про рівняння; про нерівності зі змінною. Розглянь, як учні розв’язали рівняння та нерівність способом добору. Прокоментуй їхні дії. Із чисел 1, 2, […]...

  11. Сума та різниця кубів Урок № 47 Тема. Сума та різниця кубів Мета: домогтися свідомого засвоєння змісту формул (a ± b)(a2 ab + b2) = a3 ± b3 та виробити базові вміння застосовувати ці формули для перетворень відповідних цілих виразів у багаточлен стандартного вигляду. Тип уроку: засвоєння знань. Хід уроку I. Організаційний момент @ Учитель перевіряє готовність учнів до […]...

  12. Розв’язування дробово-раціональних рівнянь УРОК 26 Тема. Розв’язування дробово-раціональних рівнянь Мета уроку: познайомити учнів з розв’язуванням дробово-раціональних рівнянь відносно тригонометричних функцій, формувати уміння учнів розв’язувати дробово-раціональні рівняння і проводити відбір коренів за допомогою одиничного кола. І. Перевірка домашнього завдання 1. Відповіді на запитання учнів, які виникли у них при виконанні домашнього завдання. 2. Розв’язування аналогічних вправ. Розв’яжіть рівняння: A) […]...

  13. Завдання для перевірки знань за курс алгебри 7 класу 1. 1) х – 2 = 5; 7 – 2 = 5; 5 = 5; 7 – корінь рівняння; 2) 56 : х = 6; 56 : 7 = 8; 8 ≠ 6; 7 – не є корінь рівняння. 2. 1) p4 • p3 = р7; 2) t9 : t5 = t4. 3. 1) х […]...

  14. Рівняння із вдома змінними 870. Рівняння із двома змінними: б) x + 2у = 7; г) х – у = 1; д) 12x + 10у = 0; е) 0x – 2у = 3; ж) 3x + 0у = 0; ж) 0x + 0у = 0; з) 0x + 0y = 1. 871. 2х – у = 3. А) x […]...

  15. Додавання і віднімання багаточленів Урок № 33 Тема. Додавання та віднімання багаточленів Мета: вдосконалити вміння учнів перетворювати суму та різницю багаточленів у багаточлен стандартного вигляду; виробити вміння виконувати обернені перетворення (заключати кілька членів багаточлена в дужки, перед якими стоїть певний знак); здійснити проміжну діагностику рівня засвоєння знань та вмінь. Тип уроку: застосування знань, умінь та навичок. Хід уроку І. […]...

  16. Ділення багатоцифрових чисел на двоцифрові круглі у випадку, коли в частці є нулі. Задачі з буквенный даними (№№ 902-910) Тема. Ділення багатоцифрових чисел на двоцифрові круглі у випадку, коли в частці є нулі. Задачі з буквенный даними (№№ 902-910). Мета. Вчити учнів ділити багатоцифрові числа на круглі двоцифрові числа; удосконалювати вміння розв’язувати рівняння, задачі з буквенимиданими. Обладнання. Таблиця “Ділення на двоцифрові числа”; картки для опитування; короткий запис задачі. Зміст уроку І. Контроль, корекція та […]...

  17. Квадратні корені Математика – Алгебра Квадратні корені Квадратні рівняння Квадратним рівнянням називається рівняння виду , де х – невідоме, a, b, c – деякі числа, причому . Числа a, b, c – коефіцієнти квадратного рівняння: a – перший коефіцієнт, b – другий коефіцієнт, c – вільний член. Якщо , рівняння називається Зведеним. Якщо ­хоча б один із […]...

  18. Розв’язання систем лінійних рівнянь способом підстановки Рівень А Відповідь: (1; 3). Відповідь: (7; -4,5). Відповідь: (1; 3). Відповідь: (4; 1). Відповідь: (3; 1). Відповідь: (1;-2). Відповідь: розв’язків немає. Відповідь: (3; 2). Відповідь: (4; 0). Відповідь: (3; 5). Відповідь: (1,5; 2). Відповідь: (3; -1). Відповідь: (7; 1). Відповідь: (1; -1). Рівень Б Відповідь: (2; 1,5). Відповідь: (1; -2). Відповідь: (20; 0,5). Відповідь: […]...

  19. Логарифмічні рівняння УРОК 57 Тема. Логарифмічні рівняння Мета уроку. Формування умінь учнів розв’язувати логарифмічні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за № 15-25 із “Запитання і завдання для повторення” розділу V та відповіді на запитання, які виник­ли в учнів у процесі виконання домашніх завдань. 2. Виконання вправ, аналогічних домашнім: № 47 (1; 3), 51. II. […]...

  20. Перетворення виразів Уроки № 122, 123 Тема. Перетворення виразів 1. Спростіть вираз і знайдіть його значення при даних значеннях букв: а) -12b – 7b + 10b – b при b = -0,1; 2; -1; -5,7; 0; Б) -5а – 8а – 2а – 15a при а = -0,6; ; ; 0,002; -1; В) -4c + 9с – […]...

  21. Рівняння та їх властивості. Розв’язування задач за допомогою рівнянь Урок № 106 Тема. Рівняння та їх властивості. Розв’язування Задач за допомогою рівнянь Мета: діагностика рівня засвоєння знань та вмінь, передбачених програмою з названої теми. Тип уроку: перевірка і корекція знань, умінь та навичок. Хід уроку I. Організаційний момент (Перевіряємо готовність до уроку, збираємо робочі зошити на перевірку; оголошуємо умову та вимоги до виконання завдань […]...

  22. Розв’язування показникових рівнянь УРОК 46 Тема. Розв’язування показникових рівнянь Мета уроку. Формування умінь учнів розв’язувати показникові рівняння способом зведення до спільної основи; способом винесення за дужки спільного множника; способом зведення до спільного показника; графічним способом. І. Перевірка домашнього завдання Два учні на відкидних дошках відтворюють розв’язування вправ відповідно № 1, 3, 5, 7, 9 і № 2, 4, […]...

  23. Показникові рівняння УРОК 45 Тема. Показникові рівняння Мета уроку. Формування умінь учнів розв’язувати найпростіші показникові рівняння. І. Перевірка домашнього завдання 1. Учитель відповідає на питання учнів, що виникли в процесі виконання домашніх завдань. 2. Самостійна робота Початковий рівень (2 бали) 1) Які з поданих функцій у = 5х; ; ; є Зростаючими? Спадними? Середній рівень (3 бали) […]...

  24. Квадратні рівняння Тестові завдання Тестове завдання № 4 . Квадратні рівняння 1. Яке з рівнянь є квадратним? А Б В Г 7х – 3 = 0 (х – 1)2 = х2 – 4х 5х2 = 4х2 2. Знайдіть коефіцієнти a, b і с квадратного рівняння 3 – х2 – 6х = 0. А Б В Г 3; […]...

  25. Раціональні числа: додавання і віднімання. Розв’язування вправ Урок № 79 Тема. Раціональні числа: додавання і віднімання. Розв’язування вправ Мета: підготувати учнів до виконати тематичної контрольної роботи. Тип уроку: узагальнення та систематизації знань, вдосконалення вмінь. Хід уроку І. Перевірка домашнього завдання @ Оскільки вправи домашнього завдання дублюють вправи, розв’язані на попередньому уроці, доцільно з метою збереження часу, перевірити вибірково зошити у “слабких” учнів […]...

  26. Квадратні корені Тестові завдання Тестове завдання № 2 . Квадратні корені 1. Значення якого з виразів є ірраціональним числом? А Б В Г 2. Знайдіть значення виразу . А Б В Г 0,5 11 10,1 1,1 3. Розв’яжіть рівняння 2у2 + 9,8 = 0 А Б В Г 0,7 Коренів немає ± 4. Визначте всі значення змінної, […]...

  27. Лінійні рівняння з одним невідомим Математика – Алгебра Рівняння Лінійні рівняння з одним невідомим Рівняння виду , де a і b – деякі числа, а х – невідоме, називається Лінійним рівнянням з одним невідомим. Числа a і b називають Коефіцієнтами. Кількість коренів лінійного рівняння 1. Якщо , лінійне рівняння має єдиний корінь: . 2. Якщо , , лінійне рівняння коренів […]...

  28. Розв’язування задач і вправ. Самостійна робота № 7 Урок № 7 Тема. Розв’язування задач і вправ. Самостійна робота № 7 Мета уроку. Формування навичок розв’язування задач на звичайні дроби, перевірити ступінь засвоєння вивченого. Хід уроку I. Перевірка домашнього завдання Учні коментують розв’язки виконаних вправ. II. Самостійна робота №9 Варіант І 1. При яких значеннях n дріб правильний? 2. Порівняй числа : а ) […]...

  29. Розв’язування вправ на застосування перетворень виразів Урок № 56 Тема. Розв’язування вправ на застосування перетворень виразів Мета: узагальнити та систематизувати знання та вміння учнів щодо різних видів перетворень цілих виразів; відпрацювати навички застосування набутих знань та вмінь під час розв’язування завдань на доведення подільності. Тип уроку: узагальнення та систематизація знань. Хід уроку I. Організаційний момент Перевіряємо готовність учнів до уроку, повідомляємо […]...

  30. Домашня самостійна робота № 2 1. А. 2. k(n – m) = kn – km. Г. 3. 4с + 8 = 4(с + 2). Б. 4. (х – 5)(х + 2) = х2 + 2х – 5х = х2 – 3х – 10. Б. 5. (3m2 – m) + (4m2 – 5) – (7m2 + 3) = 3m2 – m […]...

  31. СУМА Й РІЗНИЦЯ КУБІВ Цілі: – навчальна: удосконалити вміння застосовувати формули суми й різниці кубів до розв’язування задач; – розвивальна: формувати вміння міркувати за аналогією; сприяти удосконаленню обчислювальних навичок; – виховна: виховувати позитивне ставлення до навчання, віру у власні сили, цілеспрямованість; Тип уроку : удосконалення вмінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП ______________________________________________________ ______________________________________________________ ______________________________________________________ […]...

  32. Підсумковий урок з алгебри за 7 клас Урок № 86 Тема. Підсумковий урок з алгебри за 7 клас Мета: перевірити засвоєння передбачених програмою знань і вмінь учнів, набутих під час вивчення алгебри в 7 класі. Тип уроку: перевірка рівня засвоєння знань. Хід уроку І. Умова завдань річної контрольної роботи Варіант 1 Варіант 2 1. Спростіть вираз: A) (3m – 2)2 – 2(m […]...

  33. Корінь n-го степеня. Арифметичний корінь n-го степеня і його властивості УРОК 33 Тема. Корінь n – го степеня. Арифметичний корінь n – го степеня і його властивості Мета уроку. Повторити відомості про квадратний корінь. Формування понять корінь n-го степеня і арифметичний корінь n-го степеня. Вивчення властивостей коренів n-го степеня. І. Аналіз контрольної роботи з теми “Тригонометричні рівняння і нерівності” II. Повторення відомостей про квадратний корінь […]...

  34. Квадрат двочлена Урок № 44 Тема. Квадрат двочлена Мета: відпрацювати навички застосування формул “квадрат двочлена” у стандартних ситуаціях та вдосконалити вміння застосовувати названі формули для перетворення виразів більш високою ступеня складності. Тин уроку: застосування знань, умінь та навичок. Хід уроку І. Перевірка домашнього завдання @ № 1 є завданням базового рівня на закріплення вмінь використовувати формули “квадрата […]...

  35. Рівняння прямої УРОК № 28 Тема. Рівняння прямої Мета уроку: виведення рівняння прямої. Формування вмінь учнів використовувати рівняння прямої до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати і вектори на площині” [13]. Вимоги до рівня підготовки учнів: записують і пояснюють рівняння прямої. Розпізнають рівняння прямої. Хід уроку I. Перевірка домашнього завдання Перевірити наявність […]...

  36. РІЗНИЦЯ КВАДРАТІВ Цілі: – навчальна: сформувати стійкі вміння і навички застосовувати формулу різниці квадратів до розв’язування задач; – розвивальна: формувати вміння використовувати необхідну інформацію для розв’язування задач; сприяти удосконаленню обчислювальних навичок; – виховна: виховувати відповідальність за результати своєї роботи, дисциплінованість, працьовитість; Тип уроку : застосування знань, умінь і навичок. Обладнання та наочність: Хід уроку І. ОРГАНІЗАЦІЙНИЙ ЕТАП […]...

  37. Функція. Область визначення функції. Область значень функції Урок № 60 Тема. Функція. Область визначення функції. Область значень функції Мета: закріпити термінологію, відпрацювати навички роботи з поняттями функції; відпрацювати навички роботи із функцією, заданою формулою і таблично; знаходити функції аргументу, області визначення функції. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (традиційно) II. Перевірка домашнього завдання @ Оскільки основна частина […]...

  38. Контрольна робота № 7 (підсумкова) УРОКИ 63-70 Уроки 63-70 відповідають V розділу програми з алгебри та початків аналізу “Резерв навчального часу”, і вчитель може використовувати цей час на власний розсуд з урахуванням рівня математичної підготовки учнів. Ці години можна використати на повторення на початку на­вчального року, як додаткові години на окремі теми або для узагальнення й систематизацію матеріалу і повторення […]...

  39. Ділення УРОК 52 Тема. Ділення Мета: навчити учнів розв’язувати текстові задачі на складання рівнянь; відпрацьовувати навички розв’язування рівнянь на застосування різних правил залежностей компонентів арифметичних дій. Тип уроку: застосування вмінь та навичок. Хід уроку І. Перевірка домашнього завдання @ Для економії часу на уроці, вчитель може скористатись допомогою учнів-консультантів, які перед уроком перевірять наявність і правильність […]...

  40. Найпростіші ірраціональні рівняння УРОК 37 Тема. Найпростіші ірраціональні рівняння Мета уроку. Познайомити учнів з методами розв’язування ірраціональних рівнянь. Формування умінь розв’язувати ірраціональні рівняння. І. Перевірка домашнього завдання 1. Фронтальна бесіда за запитаннями № 38-46 із “Запитання і завдання для повторення до розділу III”. 2. Розв’язування вправ, аналогічних до домашніх. А) Обчислити . Відповідь: 3. Б) Обчислити . Відповідь: […]...

Ви зараз читаєте: Багаточлен. Дії з багаточленами
«
»