Багатогранники. Правильні багатогранники
3.
Найменша кількість ребер, що сходиться в одній вершині багатогранника – три.
4.
В одній вершині багатогранника може сходитися безліч ребер.
Розглянемо піраміду з n-кутником в основі. Яким би великим не було число п,
Завжди можна побудувати піраміду, основа якої має n + 1 вершин.
5.
Розглянемо трикутну піраміду. Кількість її ребер шість.
Шість – це найменша кількість ребер, яку може мати багатогранник.
6.
1) Куб має 12 двогранних кутів.
2) Куб має 8 тригранних кутів.
3) Куб не має чотиригранних кутів. .
4)
7.
Розглянемо тетраедр. Він має 6 двогранних кутів та чотири тригранних.
Тому найменша кількість багатогранних кутів для багатогранника – 10.
8.
1) Багатогранник, що має є вершин і 5 граней.
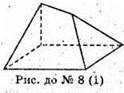
2) Багатогранник, у якого число вершин і число граней однакове.
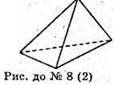
9.
Ні, не правий. В основі правильної чотирикутної призми лежить квадрат,
А в основі прямокутного паралелепіпеда – прямокутник.
10.
Так, це означення є правильним.
11.
Розглянемо призму, в основі якої лежить трикутник.
В цій призмі не можна
12.
Виходячи з означення правильної трикутної піраміди, не можна стверджувати,
Що її бічні ребра дорівнюють ребрам основи. Тому правильну трикутну піраміду
Не можна назвати правильним багатогранником.
13.
Виходячи з означення призми всі відрізки, які сполучають відповідні точки
Основ паралельні деякій прямій 1, а значить вони паралельні друг другу.
Таким чином ребра призми паралельні.
14.
В основі такої призми має лежати правильний багатокутник.
15.
Утворена фігура не буде правильним багатогранником,
Оскільки не буде виконуватися вимога стосовно того, що в кожній вершині
Сходиться одне й те саме число ребер.
16.
Ні, такого багатогранника не існує.
17.
Трикутна призма має 9 двогранних кутів.
18.
1) Багатогранник має 12 двогранних кутів.
2) Багатогранник має 24 плоских кути.
19.
Розглянемо призму, в основі якої лежить n-кутник. Порахуємо її ребра.
N ребер належить нижній основі, n ребер належить верхній основі,
А також n бічних ребер. Загальна кількість Зn, а це число кратне трьом.
Значить, твердження вірне.
20.
Оскільки число ребер призми кратне трьом (див. № 19),
То в основі призми лежить багатокутник, який має 18 : 3 = 6 граней.
Тобто в основі лежить шестикутник.
21.
1) n-кутна піраміда має (п + 1) вершину, 2n ребер (n ребер основи і n бічних ребер), (n+ 1) грань (n бічних і одна грань – основа).
2) Розглянемо n-кутну піраміду. В основі лежить n-кутник, який має n плоских кутів. Розглянемо одну з бічних граней. Це трикутник, він має З плоских кута. В піраміді n бічних граней. Для них кількість плоских кутів буде Зn, тому загальна кількість плоских кутів 4n.
.,·
22.
Розглянемо піраміду, в основі якої лежить n-кутник. Порахуємо кількість її ребер,
N-кутник має n ребер. Крім того, є ще n ребер, які сполучають вершини багатокутника основи з вершиною піраміди. Загальна кількість 2n, а це число парне.
23.
Бічні грані піраміди – трикутники. Їх n штук. Сума кутів кожного трикутника 180°. Значить сума плоских кутів бічних граней буде дорівнювати 180°n.
В основі піраміди лежить n-кутник. Сума його кутів 180 (n – 2).
Тоді сума всіх плоских кутів n-кутної піраміди 180°n + 180°(n – 2) = 360 (n – 1).
24.
Оскільки число плоских кутів n-кутної піраміди кратне 4 (див. № 21 (2)),
То піраміда не може мати 18 плоских кутів і може мати 20 плоских кутів.
25.
1) Так, інші Ірані можуть бути трикутниками. Наприклад, п’ятикутна піраміда.
2) Ні, інші грані не можуть бути чотирикутниками.