Об’єми кулі та її частини. Площа сфери
1.
Обчислимо площу поверхні Землі: S= 4πR2 = 4π · 63752.
Площа суші складає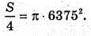
Відповідь: π × 63752.
2.
Знайдемо об’єм кавуна радіуса 10 см: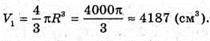 
На одного їдока приходиться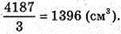 
Знайдемо об’єм кавуна-радіусом 20 см:
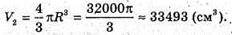
На одного їдока приходиться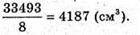 
Відповідь: у вісьмох.
3.
Оскільки передбачається, що каша у двох котлах однакова,
То в другому казані відношення води і крупи буде таке саме, як і в першому.
Відповідь:
4.
Знайдемо площу поверхні м’яча радіусом 10 см. S = 4π × 100.
Для виготовлення м’яча потрібно матеріалу: 400π × 1,1 = 440π (см2).
Відповідь: 440π см2.
5.
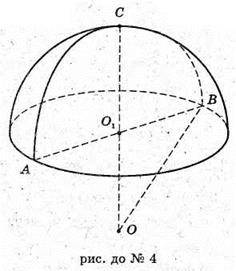
Нехай O1B – радіус сигмента, О1В = 3 см,
CO1 – висота,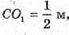 
ОВ = ОС = R.
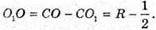З ΔО1ВО: OВ2 = О1В2 + О1О2;
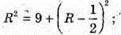
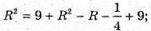
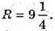
Отже, об’єм землі для клумби V дорівнює:
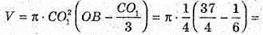
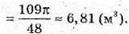
Відповідь: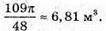 
6.
Нехай діаметр Землі дорівює D,
2R = D, d – діаметр Місяця, r – радіус Місяця;
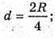
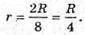
Об’єм Землі: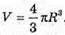 
Об’єм Місяця: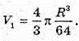 
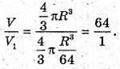
Відповідь: 64 : 1.
7.
Нехай В – діаметр Землі, d – діаметр Марса, R – радіус Землі,
Г – радіус Марса.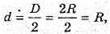 
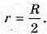
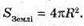
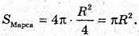
Площа поверхні Марса у 4 рази менша поверхні Землі.
8.
Знайдемо поверхню кулі радіусом R. S = 4πR2.
Знайдемо поверхню кулі радіусом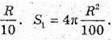 
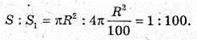
Відповідь: 100 куль.
9.
Нехай r – радіус маленької кульки, R – радіус великої кулі. R = 5r.
Об’єм однієї кульки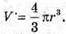 
Об’єм великої кулі 
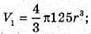V1 : V = 125.
Отже, для виготовлення великої кулі треба переплавити 125 маленьких кульок.
10.
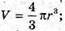3V = 4πr3;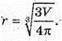 
Відповідь: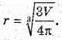 
11.
1) S = 4πR2 = 4π × 16 = 64π (см2);
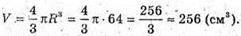
2) 
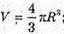3V = 4πR3; 12 000 = 4πR3;
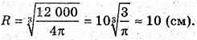
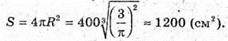
3) S = 4πR2; 4πR2 = 64π;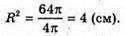 
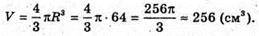
Відповідь: 1) 64π см2;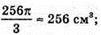 
2) 
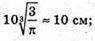
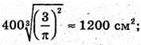3) 4 см;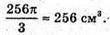 
12.
Нехай V1 – об’єм першої частини кулі, V2- об’єм другої частини кулі.
V1 = 720π см3, V2 = 252π см3.
Об’єм V кулі дорівнює: V= V1 + V2 = 720π + 252π = 972π (см3).
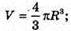3V = 4πR3; 3 · 972π = 4 πR 3; R3 = 729; R = 9.
S = 4 πR 2 = 4π × 81 = 324π (см 2).
Відповідь: 324π см2.
13.
1) Нехай сфера задана рівнянням х2 + у2 + z2 = 3, отже,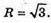 
S = 4πr2 = 4π × 3 = 12π.
2) Нехай сфера задана рівнянням (х – 1)2 + (у + 1)2 + (z – 2)2 = 16,
Отже, R = 4. S = 4πг2 = 4π × 16 = 64π.
3) х2 + 2х + у2 + z2 = 0; x 2 + 2x + 1 + у2 + z2= 1; (х + 2)2 + у2 + z = 1.
S = 4πr2 = 4π.
4) x 2 – 2х + у2 + 2у + z2- 4z = 3; x2 – 2х + 1 + у2 + 2у + 1 + z2 – 4z + 4 = 9;
(x – 1)2 + (у + 1)2 + (z – 2)2 = 9; R = 3. S = 4πг2 = 4π × 9 = 36π.
14.
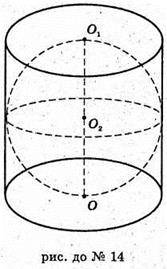
Якщо циліндр, описаний навколо кулі, то цей циліндр рівнобокий.
Нехай R – радіус кулі, тоді радіус циліндра дорівнює R, а висота циліндра 2R.
Sциліндра = 2 πR × 2R + 2 πR 2 = 6 πR2; Vциліндра = πR 2 × 2R = 2 πR 3
Sкулі = 4 πR2: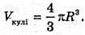 
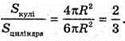
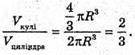
Твердження доведено.
15.
Нехай V1- об’єм першого циліндра, V2 – об’єм другого;
R1Н1 – виміри першого циліндра; R2, Н2 – виміри другого циліндра.
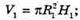
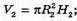V1 = V2
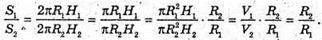
Твердження доведено.
16.
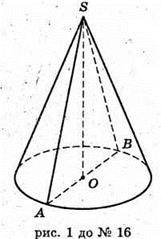
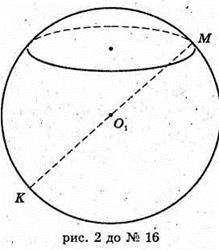
Нехай SO = KM, АВ = AS.
З ΔSAO: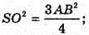 
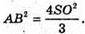
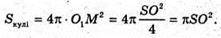
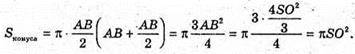
Отже, Sкулі = Sконуса
17.
Нехай S – площа поверхні кулі, S1- площа поверхні другої кулі,
S = 43 см2. S = 4πR2; 43 = 4πR2;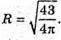 
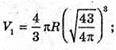
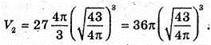
Знайдемо радіус другої кулі:
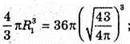
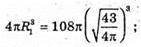
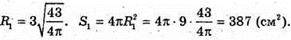
Відповідь: 387 см2.
18.
Нехай S1- площа поверхні кулі, S2 – площа поверхні другої кулі,
S1 = 393 см2.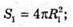 
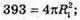
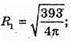
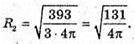
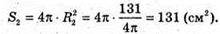
Відповідь: 131 см2.
19.
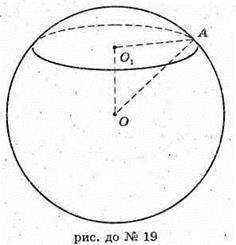
Нехай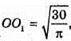 
S1 – площа перерізу. S1 = π × O1A2; 15 = π × Ο1A2;
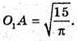З ΔО1АО: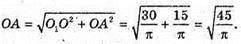 
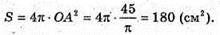
Відповідь: 180 см2.
20.
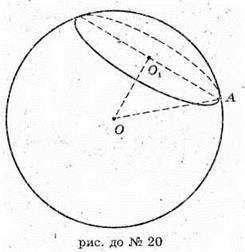
Нехай ∠ОАО1 = 45°, ОА – радіус кулі. Проведемо OO1 + О1А.
S = 4π × ОА2; 4π × ОА2 = 125;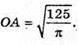 
ΔО1АО – прямокутний,
∠Ο1ΑΟ = ∠ΑΟΟ1 = 45°.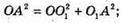 
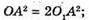
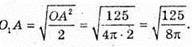
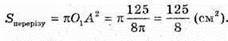
Відповідь: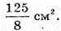 
21.
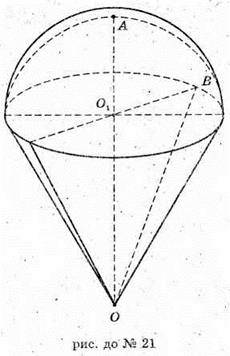
Нехай Ο1Β = 60 cм, OB = 75 cм.
3 ΔΟ1ΒΟ: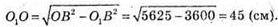 
AO 1 = OB – O1O = 75 – 45 = 30 (cм).
Отже, об’єм кульового сектора дорівнює:
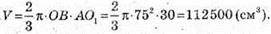
Відповідь: 112 500 см3.
22.
Нехай об’єм кулі S = 36π см2.
Якщо площина проходить через центр кулі, то вона ділить кулю на дві рівні півкулі.
Площа поверхні кожної з утворених частин складається з площі поверхні півкулі і січної площини, яка проходить через діаметр кулі.
S = 4 πR 2; 36π = 4 πR2;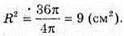 
Площа січної площини S1 = π × R2 = 9π (см2).
Площа півкулі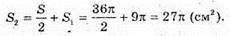 
Відповідь: 26π см2.
23.
Нехай ∠ASO = α, АО = R, SO1 = r.
З ΔSAO: SO= АО × ctg∠ASO = R × ctg α. ОО1 = SO – SO1 = R ctg α – r.
З ΔΑΟ1Ο: AO12 = ОО12 + AO; r2 = (R ctg α – r)2 + R2;
R2 = R2 ctg2α – 2Rrctg α + r2 + R2; 2Rr ctg α = R2 ctg2α + R2; 2Rr ctg α = R2(ctg 2 α + 1).
(1 votes, average: 5.00 out of 5)
Loading...