Ділення
Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ
§ 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ
18. Ділення
Дію ділення означають за допомогою дії множення. Наприклад, поділити число 51 на 17 – це означає знайти таке число, добуток якого з числом 17 дорівнює 51. Маємо: 17 ∙ 3 = 51, тому 51 : 17 = 3.
Узагалі, для натуральних чисел а, b і с рівність а : b = с є правильною, якщо правильна рівність b ∙ с = а.
Розглянемо ще кілька прикладів:
168 : 12 = 14, оскільки 12 ∙ 14 = 168;
1197 : 21 = 57, оскільки 21 ∙ 57 = 1197.
У рівності а : b = с число а називають діленим, число b – дільником,
Частка а : b показує, у скільки разів число а більше за число b або у скільки разів число b менше від числа а.
Чи можна, наприклад, обчислити частку 11 : 0? Якщо припустити, що така частка існує і дорівнює деякому числу с, то має виконуватися рівність 0 ∙ с = 11, але насправді 0 ∙ с = 0. Отже, обчислити частку 11:0 неможливо.
А чи можна обчислити частку 0 : 0? Нехай 0 : 0 = с. Тоді 0 ∙ с = 0. Така рівність справедлива за будь-якого с. А це означає, що значенням числового виразу 0 : 0 може бути будь-яке число, тобто таку частку обчислити неможливо.
Отже, робимо висновок: на нуль ділити не можна. Разом
0 : а = 0
Для будь-якого натурального числа а справедливі рівності:
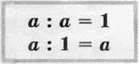
Ці рівності легко перевірити за допомогою множення. Переконайтеся в цьому самостійно.
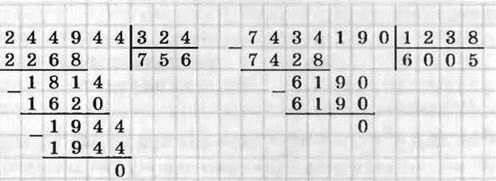
Ви вмієте ділити письмово (куточком) багатоцифрове число на двоцифрове. Аналогічно виконують ділення будь-яких багатоцифрових чисел, наприклад:
ПРИКЛАД 1 Розв’яжіть рівняння 12x = 84.
Розв’язання. Застосуємо правило знаходження невідомого множника: щоб знайти невідомий множник, треба добуток поділити на відомий множник. Маємо: x = 84 : 12;
X = 7.
Відповідь: 7.
ПРИКЛАД 2 Розв’яжіть рівняння x : 21 = 16.
Розв’язання. Застосуємо правило знаходження невідомого діленого: щоб знайти невідоме ділене, треба дільник помножити на частку.
Маємо: х = 21 ∙ 16;
Х = 336.
Відповідь: 336.
ПРИКЛАД 3 Розв’яжіть рівняння 576 : х = 18.
Розв’язання. Застосуємо правило знаходження невідомого дільника: щоб знайти невідомий дільник, треба ділене поділити на частку.
Маємо: х = 576 : 18;
Х = 32.
Відповідь: 32.
ПРИКЛАД 4 Моторний човен проходить відстань між двома пристанями, яка дорівнює 64 км, проти течії річки за 8 год. За скільки годин він пройде цю відстань за течією річки, якщо швидкість течії дорівнює 4 км/год?
Розв’язання. 1) 64 : 8 = 8 (км/год) – швидкість човна проти течії.
2) 8 + 4 = 12 (км/год) – власна швидкість човна.
3) 12 + 4 = 16 (км/год) – швидкість човна за течією.
4) 64 : 16 = 4 (год) – час руху за течією. Відповідь: 4 год.
ПРИКЛАД 5 Із двох міст, відстань між якими дорівнює 588 км, виїхали назустріч один одному два автомобілі, які зустрілися через 6 год після початку руху. Швидкість одного автомобіля становила 46 км/год. Знайдіть швидкість другого автомобіля.

Розв’язання. 1) 588 : 6 = 98 (км) – на стільки зменшується відстань між ними щогодини.
2) 98 – 46 = 52 (км/год) – швидкість другого автомобіля.
Відповідь: 52 км/год.
ПРИКЛАД б Відстань між двома селищами дорівнює 24 км. Із цих селищ одночасно в одному напрямі вирушили пішохід і велосипедист. Попереду йшов пішохід. Через скільки годин після початку руху велосипедист наздогнав пішохода, якщо пішохід ішов зі швидкістю
4 км/год, а велосипедист їхав зі швидкістю 12 км/год?
Розв’язання. 1)12-4 = 8 (км) – на стільки зменшувалася відстань між велосипедистом і пішоходом щогодини.
2) 24 : 8 = 3 (год) – час, за який велосипедист наздогнав пішохода.
Відповідь: 3 год.
ПРИКЛАД 7 Івасик розв’язав у 3 рази більше задач з алгебри, ніж з геометрії. Скільки задач з геометрії розв’язав Івасик, якщо відомо, що їх було на 18 задач менше, ніж з алгебри?
Розв’язання. Нехай Івасик розв’язав х задач з геометрії, тоді з алгебри він розв’язав 3x; задач. Оскільки за умовою задачі х на 18 менше від 3x, то 3x – х = 18.
Тоді 2х = 18.
Звідси х = 18 : 2; х = 9.
Відповідь: 9 задач.
ПРИКЛАД 8 Фермери Гречуха, Медовий і Запашний зібрали на своїх полях 600 кг полуниць. Медовий зібрав у 2 рази більше, ніж Гречуха, а Запашний – на 128 кг більше, ніж Гречуха. Скільки кілограмів полуниць зібрав кожний фермер?
Розв’язання. Нехай Гречуха зібрав х кг полуниць, тоді Медовий зібрав 2х кг, а Запашний – (x + 128) кг. Оскільки разом вони зібрали 600 кг, то складемо рівняння:
Х + 2х + х + 128 = 600.
Тоді
4х + 128 = 600;
4х = 600 – 128;
4х = 472; х = 472 : 4; х = 118.
Отже, Гречуха зібрав 118 кг полуниць,
Медовий зібрав 2 ∙ 118 = 236 (кг),
А Запашний зібрав 118 + 128 = 246 (кг).
Відповідь: 118 кг, 236 кг, 246 кг.
Розв’язуємо усно
1. Заповніть ланцюжок обчислень:

2. Виконайте ділення:
1) 432 : 4; 2) 609 : 3; 3) 3600 : 6; 4) 1500 : 50.
3. Укажіть серед даних добутків найбільший:
1) 239 ∙ 4 ∙ 25; 3) 10 ∙ 239 ∙ 10;
2) 239 -20-4; 4) 239 ∙ 10 ∙ 12.
4. Доганяючи Сашка, Славко біжить зі швидкістю 180 м/хв. Чому дорівнює швидкість Сашка, якщо хлопчики зближуються зі швидкістю 12 м/хв?
5. Два автомобілі рухаються назустріч один одному, причому один із них зі швидкістю 74 км/год. Чому дорівнює швидкість другого автомобіля, якщо вони зближуються зі швидкістю 150 км/год?
Вправи
452.° Відомо, що 243 ∙ 425 = 103 275. Чому дорівнює значення виразу:
1) 103 275 : 243; 2) 103 275 : 425?
453.° Відомо, що 4608 : 48 = 96. Чому дорівнює значення виразу:
1) 96 ∙ 48; 2) 4608 : 96?
454.° Заповніть таблицю:
Ділене | 320 | 96 | 0 | 945 | 637 | 3232 |
Дільник | 40 | 6 | 264 | 128 | 1 | 16 |
Частка | 8 | 14 | 0 | 1 |
455. Виконайте ділення:
1) 1548 : 36; 4) 3672 : 34; 7) 16 320 : 48;
2) 2668 : 58; 5) 15 552 : 72; 8) 906 192 : 126;
3) 5562 : 18; 6) 16 728 : 68; 9) 942 866 : 178.
456.° Виконайте ділення:
1) 2812 : 74; 4) 9384 : 46; 7) 63 378 : 63;
2) 1248 : 24; 5) 18 526 : 59; 8) 153 216 : 38;
3) 6565 : 13; 6) 15 652 : 26; 9) 1 334 504 : 214.
457.° Виконайте ділення:
1) 34 250 000 : 10; 5) 25 600 : 800;
2) 34 250 000 : 1000; 6) 2 430 000 : 180;
3) 34 250 000 : 10 000; 7) 2 430 000 : 1800;
4) 25 600 : 80; 8) 2 430 000 : 18 000.
458.° Виконайте ділення:
1) 32 596 800 : 10; 4) 450 000 : 150;
2) 876 900 : 100; 5) 36 000 : 12 000;
3) 240 000 : 10 000; 6) 124 360 000 : 40 000.
459.° Виконайте дії:
1) 256 + 144 : 16 – 8; 3) (256 + 144) : 16 – 8;
2) (256 + 144) : (16 – 8); 4) 256 + 144 : (16 – 8).
460.° Знайдіть значення виразу:
1) 4704 – 4704 : (46 + 38); 2) 2808 : 72 + 15 808 : 52.
461.Знайдіть значення виразу:
1) 3264 – 3264 : (92 – 44);
2) 18 144 : 84 – 2924 : 68.
462.° Розв’яжіть рівняння:
1) 13x = 195; 4) 33m – m = 1024;
2) x ∙ 18 = 468; 5) x : 19 = 26;
3) 11x + 6x = 408; 6) 476 : x = 14.
463.° Розв’яжіть рівняння:
1) 19x = 95; 4 )у + 27 у = 952;
2) x ∙ 22 = 132; 5) x : 25 = 16;
3) 38x – 16x = 1474; 6) 324 : x = 27.
464.° Вершник долає відстань між двома селищами за 5 год, якщо рухається зі швидкістю 12 км/год. З якою швидкістю він має рухатися, щоб подолати цю відстань за 4 год?
465.° Петрик купив 8 кг печива по 36 грн за кілограм. Скільки кілограмів печива по 24 грн за кілограм він зможе купити за ці самі гроші?
466.° Знайдіть значення виразу:
1) 82 275 – 64 ∙ 56 + 9680 : 16 – 23 637;
2) (204 ∙ 402 – 30 456 : 423) : 36 – 1388;
3) 1376 : (621 – 589) + (138 – 69) ∙ 29.
467.∙ Знайдіть значення виразу:
1) 49 184 + 4575 : 15 – 62 ∙ 93 – 33 999;
2) (306 ∙ 307 – 187 ∙ 36) : 45 + 5780;
3) 1885 : (542 – 477) + 48 ∙ (134 – 92).
468.∙ Малюк купив для Карлсона 8 тістечок і 12 булочок з повидлом, заплативши за всю покупку 408 крон. Одне тістечко коштує 24 крони. Скільки коштує одна булочка?
469.° Дід Панас заготовив на зиму 6 діжок квашеної капусти і 14 діжок солоних огірків. В одну діжку вміщується 26 кг капусти. Скільки кілограмів огірків міститься в одній діжці, якщо всього дід Панас заготовив 324 кг овочів?
470.° Скільки кілограмів масла можна виготовити з 261 кг вершків, якщо з 9 кг вершків отримують 2 кг масла?
471.° У Петра Івановича є автомобіль “Таврія”. Чи вистачить йому 28 л бензину, щоб доїхати з Києва до Полтави, відстань між якими 337 км, якщо витрата бензину на проїзд 100 км становить 7 л?
472.° Курочка Ряба зібрала 328 кг проса. Скільки пшона вона зможе отримати із цього проса, якщо з 4 кг проса виходить 3 кг пшона?
473.° Відстань між двома пристанями дорівнює 476 км. Рухаючись за течією річки, катер проходить цю відстань за 14 год. За скільки годин він пройде цю відстань проти течії річки, якщо швидкість течії дорівнює 3 км/год?
474.° Відстань між двома портами дорівнює 504 км. Рухаючись проти течії річки, теплохід проходить цю відстань за 21 год. За скільки годин він пройде цю відстань за течією річки, якщо швидкість течії дорівнює 2 км/год?
475.° Із сіл Квіткове і Казкове, відстань між якими дорівнює 136 км, виїхали одночасно назустріч один одному козаки Шибайголова та Гострошабленко. Шибайголова рухався зі швидкістю 16 км/год. З якою швидкістю їхав Гострошабленко, якщо козаки зустрілися через 4 год після виїзду?

476.° Відстань між двома містами дорівнює 1264 милі1. Із них одночасно вилетіли назустріч один одному два килими-літаки й зустрілися через 8 год після вильоту. Один із килимів пролітав 82 милі за годину. З якою швидкістю летів другий килим?
477.° О 6 год ранку з Мурома до Києва виїхав зі швидкістю 9 км/год Ілля Муромець. О 8 год ранку з Мурома до Києва виїхав Альоша Попович, який наздогнав Іллю Муромця о 2 год дня. З якою швидкістю рухався Альоша Попович?
478.° О 8 год 57 хв черепаха Катріна вирушила в подорож зі свого ставка до сусіднього. О 9 год 5 хв із цього ж ставка в тому самому напрямі вирушила черепаха Вікторія, яка наздогнала Катріну о 9 год 29 хв. Знайдіть швидкість, з якою рухалася Катріна, якщо відомо, що Вікторія повзла зі швидкістю 8 м/хв.
479.° Із двох станцій, відстань між якими дорівнює 24 км, одночасно в одному напрямі вийшли два поїзди. Попереду йшов поїзд зі швидкістю 58 км/год. Через 4 год після початку руху його наздогнав другий поїзд. Знайдіть швидкість другого поїзда.
480°Відстань між селами Вишневе та Яблуневе дорівнює 15 км. Із цих сіл одночасно в одному напрямі вирушили козаки Чорновус і Сірошапка. Чорновус скакав на коні зі швидкістю 9 км/год і через 3 год після початку руху наздогнав Сірошапку, який ішов пішки. З якою швидкістю йшов Сірошапка?
481.° Відстань між містечками Сен-Жермен і Сен-Антуан дорівнює 12 льє2. Із цих містечок одночасно в одному напрямі виїхали Портос зі швидкістю 1 льє/год і д’Артаньян зі швидкістю 3 льє/год, причому Портос рухався попереду. Через скільки годин після виїзду д’Артаньян наздогнав Портоса?
1 1 сухопутна миля = 1609 м.
2 Льє – старовинна французька одиниця довжини (1 льє приблизно дорівнює 4444 м).
482.° Відстань між островами Акулячий і Китовий дорівнює 48 морських миль1. Від цих островів одночасно в одному напрямі вирушили фрегати “Відважний” і “Стрімкий”, причому “Відважний” ішов попереду “Стрімкого”. “Відважний” проходив за годину 12 миль, а “Стрімкий” – 18 миль. Через скільки годин “Стрімкий” наздогнав “Відважного”?
483.° Школярі Василько, Андрійко, Данилко і Сергійко зібрали 326 кг моркви. Василько зібрав 37 кг моркви, що в 3 рази менше, ніж Андрійко, а Данилко і Сергійко зібрали моркви порівну. Хто зі школярів зібрав більше моркви?
484.° Робітники Іван, Петро, Степан і Павло виготовили 160 деталей. Іван виготовив 81 деталь, що у 3 рази більше, ніж Петро, а Степан і Павло виготовили деталей порівну. Хто з робітників виготовив найменше деталей?
485.° Буратіно живе на відстані 1 км 200 м від школи. Уроки в школі починаються о 8 год 30 хв. Буратіно робить за хвилину 120 кроків, довжина кроку – 40 см. О котрій годині Буратіно має виходити з дому, щоб приходити до школи за 10 хв до початку занять?
486.° Чергові першого загону туристів за 6 хв можуть почистити 24 картоплини, а чергові другого загону за 9 хв – 45 картоплин. За скільки хвилин спільної роботи вони почистять 198 картоплин?
487.° На скільки днів шкільній їдальні вистачить 800 л соку, якщо хлопчики за 8 днів випивають 960 л соку, а дівчатка за 6 днів – 480 л?
488.° За 4 дні роботи три оператори набрали на комп’ютері разом 288 сторінок. Скільки сторінок набере один оператор за 7 днів, якщо в них однакова продуктивність праці?
1 1 морська миля = 1852 м.
489.° Для роботи 6 однакових двигунів протягом 8 год потрібно 672 л палива. На скільки годин роботи вистачить одному такому двигуну 98 л палива?
490.° Білочки Руденька та Жовтенька збирали горіхи. Руденька зібрала 6 мішечків горіхів, а Жовтенька – 7 таких самих мішечків. Разом вони зібрали 52 кг горіхів. Скільки кілограмів горіхів зібрала Руденька і скільки – Жовтенька?
491.°Рухаючись пустелею протягом 3 днів, караван подолав 63 км. Першого дня караван рухався 6 год, другого – 8 год, а третього – 7 год. Скільки кілометрів проходив караван кожного дня, якщо відомо, що він рухався всі дні зі сталою швидкістю?
492.° Дід Часник привіз на ринок 420 кг яблук і 180 кг груш у 50 однакових ящиках. Скільки було ящиків з яблуками і скільки – з грушами?
493.° Алі-Баба перевозив знайдене в печері розбійників золото на 4 віслюках у 22 однакових мішках. На першого віслюка він навантажив 80 кг золота, на другого – 100 кг, на третього – 120 кг, на четвертого – 140 кг. Скільки мішків золота було навантажено на кожного віслюка?

494.° Розв’яжіть рівняння:
1) 21 (18 + х) = 714; 3) 12 (152 + 19x) = 2052;
2) 16 (4x – 34) = 608; 4) (152x + 32) ∙ 6 = 192.
495.° Розв’яжіть рівняння:
1) 8 (x – 14) = 56; 3) 9 (143 – 13x) = 234;
2) (46 – x) ∙ 19 = 418; 4) 17 (5x – 16) = 238.
496.° Розв’яжіть рівняння:
1) 14 x + 4х – 48 = 240;
2) 256 – 7b – 9 = 279;
3) 16а – 7а + 96 = 222;
4) 20y + 5y + у + 19 = 227.
497.° Розв’яжіть рівняння:
1) 96 + 66 – 15 = 615;
2) 17x – x + 5x – 19 = 170.
498.° Розв’яжіть рівняння:
1) (x + 14) : 9 = 13; 4) 52 + 72 : x = 56;
2) 966 : (x + 17) = 23; 5) 56 : (x – 6) = 8;
3) x : 8 – 6 = 49; 6) 56 : x – 6 = 8.
499.° Розв’яжіть рівняння:
1) (x – 23) : 26 = 8; 2) 1728 : (56 – x ) = 36.
500.° Батько із сином посадили 108 кущів помідорів, причому батько посадив у 2 рази більше, ніж син. Скільки кущів помідорів посадив сип?
501.° До двох магазинів завезли 268 кг шампіньйонів, причому до першого магазину завезли шампіньйонів у 3 рази менше, ніж до другого. Скільки кілограмів шампіньйонів завезли до кожного магазину?
502.° У султана було двогорбих верблюдів у 7 разів більше, ніж одногорбих. Скільки в султана було одногорбих верблюдів, якщо відомо, що їх на 156 менше, ніж двогорбих?
503.° Валентин подарував Валентині троянди й орхідеї, причому орхідей було в 4 рази менше, ніж троянд. Скільки троянд подарував Валентин, якщо відомо, що їх було на 51 більше, ніж орхідей?
504.° 3 вершини прямого кута проведено промінь так, що він ділить прямий кут на два кути, один з яких більший за другий на 20°. Знайдіть величину кожного з утворених кутів.
505.° 3 вершини розгорнутого кута проведено промінь так, що він ділить розгорнутий кут на два кути, один з яких менший від другого на 50°. Знайдіть величину кожного з утворених кутів.
506.° На день народження Вінні-Пуху порося П’ятачок, віслюк Іа та кенгуру Кенга подарували 264 кг меду. П’ятачок подарував у 3 рази більше меду, ніж Кенга, а Іа – у 2 рази більше, ніж Кенга. Скільки меду подарував кожен із гостей?
507.° За чотири дні подорожі Сіндбад-мореплавець проплив 546 миль. За другий день він проплив у 4 рази більше, ніж за перший, за третій – у 3 рази більше, ніж за перший, а за четвертий – у 5 разів більше, ніж за перший. Скільки миль пропливав Сіндбад кожного дня?
508.° Тарас, Богдан і Олесь зловили 256 окунів. Тарас зловив у 3 рази більше окунів, ніж Богдан, а Олесь – стільки, скільки Тарас і Богдан разом. Скільки окунів зловив найкращий рибалка?
509.° Червона Шапочка, Мальвіна, Попелюшка та Дюймовочка зліпили 500 вареників. Червона Шапочка зліпила у 2 рази більше вареників, ніж Дюймовочка, Мальвіна – стільки, скільки Червона Шапочка та Дюймовочка разом, а Попелюшка – стільки, скільки Мальвіна та Дюймовочка разом. Скільки вареників зліпила кожна дівчинка?
510.° У трьох вагонах електропоїзда їхало 246 пасажирів. У першому вагоні було у 2 рази більше пасажирів, ніж у другому, а в третьому – на 78 пасажирів більше, ніж у другому. Скільки пасажирів їхало в кожному вагоні?
511.° Між трьома школами розподілили 552 кг апельсинів, причому одна школа отримала в 6 разів менше апельсинів, ніж друга, і на 136 кг менше, ніж третя. Скільки кілограмів апельсинів отримала кожна школа?
512.° Одна зі сторін трикутника в 5 разів менша від другої і на 25 см менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 74 см.
513.° Одна зі сторін трикутника у 2 рази більша за Другу сторону, а друга – на 7 дм менша від третьої. Знайдіть сторони трикутника, якщо його периметр дорівнює 99 дм.
514.° 1) Чи правильно, що коли кожний доданок ділиться на деяке число, то й сума цих доданків ділиться на це число? Проілюструйте свою відповідь прикладами.
2) Чи може сума кількох доданків ділитися на деяке число, якщо кожний доданок не ділиться на це число? Проілюструйте свою відповідь прикладами.
515.° Як зміниться частка, якщо:
1) ділене збільшити в 7 разів;
2) ділене зменшити у 2 рази;
3) дільник збільшити в 4 рази;
4) дільник зменшити в 5 разів;
5) ділене збільшити у 8 разів, а дільник – у 2 рази;
6) ділене зменшити в 9 разів, а дільник – у 3 рази;
7) ділене збільшити в 6 разів, а дільник зменшити у 2 рази;
8) ділене зменшити в 6 разів, а дільник збільшити у 2 рази?
516.° Ділене збільшили в 3 рази. Як треба змінити дільник, щоб частка: 1) збільшилась у 6 разів;
2) зменшилась у 6 разів; 3) не змінилася?
517.°° При яких значеннях а є правильною рівність:
1) 12 : а = 12; 4) 16 : а = 1; 7) 16 : а = 0;
2) а : 15 = 1; 5) 1 : а = 1; 8) а : а = 0;
3) а : 1 = 10; 6) а : 9 = 0; 9) 0 : а = 5?
518.°° Обчисліть зручним способом:
1) (44 ∙ 58) : 11; 4) (350 ∙ 48) : 70;
2) (69 ∙ 60) : 30; 5) (2 ∙ 17 ∙ 14) : 28;
3) (63 ∙ 88) : 21; 6) (21 ∙ 18) : 14.
519.° Обчисліть зручним способом:
1) (36 ∙ 21) : 12; 3) (5 ∙ 6 ∙ 78) : 3;
2) (40 ∙ 420) : 60; 4) (45 ∙ 63) : 81.
520.°° Поставте в записі 7∙9+12:3-2 дужки так, щоб значення отриманого виразу дорівнювало: 1) 75; 2) 23.
521.°° Поставте в записі 4 ∙ 12 + 18 : 6 + 3 дужки так, щоб значення отриманого виразу дорівнювало: 1) 50; 2) 72.
522.°° Складіть числовий вираз із використанням тільки знаків чотирьох арифметичних дій та чотирьох цифр 2 так, щоб значення отриманого виразу дорівнювало:
1)1; 3)3; 5)5; 7)8;
2) 2; 4) 4; 6) 6; 8) 10.
Вправи для повторення
523. Периметр чотирикутника ABCD дорівнює 34 см, АВ = 6 см, сторона ВС у 2 рази більша за сторону АВ, сторони CD і AD рівні. Обчисліть довжину сторони AD.
524. Серед придбаних конвертів 18 виявились рожевого кольору, а 12 конвертів – з марками. Крім того, серед рожевих конвертів 8 було з марками. Скільки всього купили конвертів?
Задача від Мудрої Сови
525. На столі розташовано 7 зубчастих коліс так, що перше зчеплене з другим, друге – з третім і т. д., а сьоме зчеплене з першим. Чи можуть усі колеса обертатись одночасно?