Головна ⇒ 📌Математика ⇒ ДІЛЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ

ДІЛЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ

Розділ 2 ЗВИЧАЙНІ ДРОБИ ТА ДІЇ З НИМИ

§ 10. ДІЛЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ

Ви знаете, що невідомий множник знаходять діленням добутку на відомий множник. Наприклад, у прямокутника з площею 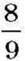дм2 й однією зі сторін 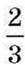дм (мал. 9) друга сторона дорівнює частці від ділення дробу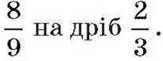

Мал. 9

Нехай шуканою часткою є дріб 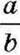. Тоді можемо записати: 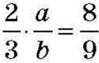. Звідси видно, що а = 4, b = 3, оскільки

2 ∙ 4 = 8, 3 ∙ 3 = 9. Отже,

ДІЛЕННЯ ДРОБІВ. ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ДРОБОМ

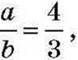тобто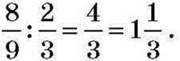

Такий самий результат дістанемо, коли дріб помножимо на дріб , який є оберненим до дробу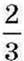

Справді: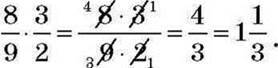

Виходить, що дію ділення дробу на дріб можна замінити дією множення даного дробу на число, обернене до дільника:

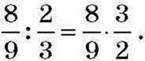
У цьому й полягає правило ділення дробу на дріб.

Правило ділення звичайних дробів

Щоб поділити звичайний дріб на звичайний дріб, треба:

1) знайти дріб, обернений до дільника;

ділене помножити на дріб, обернений до дільника.

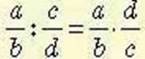
Задача 1. Поділіть дріб

Розв’язання.

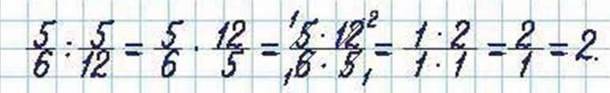
? Як поділити натуральне або мішане число на дріб? Спочатку треба дане натуральне або мішане число перетворити в неправильний дріб, а потім застосувати правило ділення дробів.

Задача 2. Знайдіть частку чисел: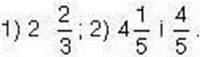

Розв’язання.

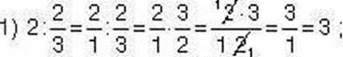
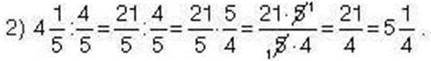
Що отримаємо, якщо 1 поділимо на деякий дріб? Отримаємо дріб, обернений до даного. Наприклад: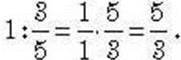

Зверніть увагу:

Якщо 1 поділити на дріб, то отримаємо дріб, обернений до даного.

Що отримаємо, якщо 0 поділимо на деякий дріб?

Отримаємо нуль. Наприклад: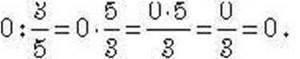

? Чи можна поділити дріб на 0? Ні, оскільки на нуль ділити не можна.

На практиці нерідко доводиться за відомою частиною величини знаходити саму величину. Ви знаєте, що це задачі на знаходження числа за його дробом. Усі вони зводяться до дії ділення числа на дріб. Розглянемо приклад.

Задача 3. Мама спекла рулет. Тетянка та Іванко виміряли рулеті відокремили частину завдовжки 30 см. Виявилося, що вони відокремили рулету. Скільки сантиметрів становила довжина цілого рулету?

Розв’язання. Якщо поділити весь рулет на 6 частин, то довжина п’яти таких частин дорівнює 30 см. Значить, довжина однієї його частини становить 30 : 5 = б (см) (мал. 10), а цілий рулет має довжину 6 ∙ 6 = 36 (см).

Такий самий результат дістанем о, якщо число 30 поділимо на дріб 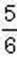, тобто: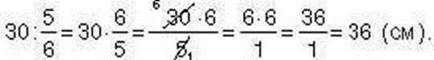

Отже, довжина цілого рулету становила 36 см. Можемо сформулювати правило.

Мал.

Запам’ятайте!

Правило знаходження числа за його дробом

Щоб знайти число за його дробом, треба дане число, що виражає частину шуканого, поділити на цей дріб.

Нехай дано два такі натуральні числа, що сума всіх дільників першого (за винятком самого числа) дорівнює другому числу, а сума всіх дільників другого числа (за винятком самого числа) дорівнює першому числу. Числа, які мають таку властивість, називають дружніми числами. Наприклад, число 220 має такі дільники: 1, 2,4, 5,10,11, 20, 22, 44, 55, 110. Їх сума дорівнює 284. Число 284 має такі дільники: 1, 2,4, 71,142. їх сума дорівнює 220. Отже, числа 220 і 284 є парою дружніх чисел. Це пара найменших дружніх чисел. Ось інші пари дружніх чисел: 1184 і 1210,2620 і 2924, 5020 і 5564, 6232 і 6368, 10744 і 10856,12285 і 14595,17296 118416, 63020 і 76084.

ПРИГАДАЙТЕ ГОЛОВНЕ

1. Сформулюйте правило ділення звичайного дробу на звичайний дріб.

2. Як знайти частку натурального числа і дробу; мішаного числа і дробу?

3. Як знайти число за його дробом?

РОЗВ’ЯЖІТЬ ЗАДАЧІ

408′. Чи правильно, що оберненим до дробу 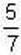є дріб:

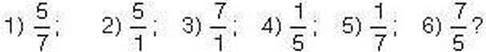
409′. Чи правильно Оленка продовжувала виконання дії: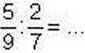

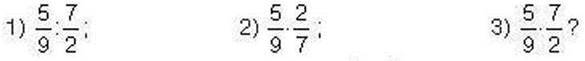
410′. Чи правильно, що частка чисел 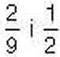дорівнює:

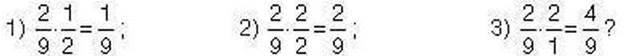
411′. Чи правий Сергійко в тому, що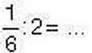

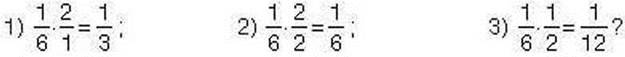
412. Чи правильно, що дорівнює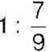

413°. Обчисліть:

414°. Знайдіть частку чисел:

415 . Знайдіть помилку в обчисленнях:

416°. Знайдіть значення виразу 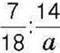, якщо:

1) а = 3; 2)а = 9; 3)а=12; 4)а = 36.

417°. Знайдіть значення виразу 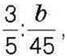якщо:

1)6 = 9; 2)6=15; 3)6=18; 4)6 = 33.

418°. Уставте замість * таке число, щоб отримати правильну рівність:

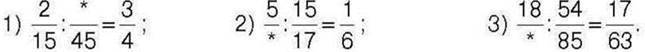
419°. Розв’яжіть рівняння:

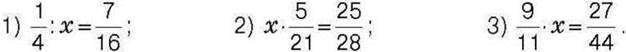
420°. Розв’яжіть рівняння:

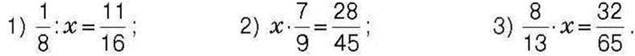
421°. Знайдіть множник, якщо інший множник дорівнює 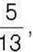а добуток –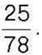

422°. Обчисліть:

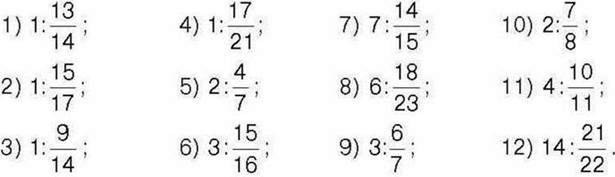
423°. Обчисліть:

424°. Розв’яжіть рівняння:

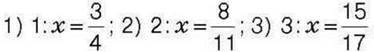
425°. Розв’яжіть рівняння:

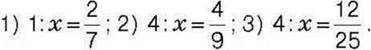
426°. У п’ятикутнику всі сторони рівні. Знайдіть сторону п’ятикутника, якщо його периметр дорівнює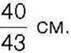

427°. У магазин привезли 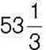кг мандаринів у n однакових ящиках. Скільки кілограмів мандаринів у кожному ящику, якщо:

1)n = 4; 2)n = 5; 3)n = 8?

428°. Обчисліть:

429°. Обчисліть:

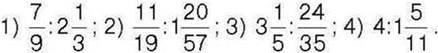
430°. Розв’яжіть рівняння:

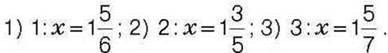
431°. Розв’яжіть рівняння:

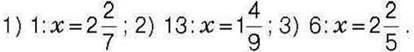
432°. Знайдіть дільник, якщо 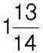– ділене, а 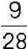– частка.

433°. Знайдіть сторону квадрата з периметро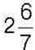м см.

434°. Знайдіть сторону прямокутника, якщо його площа дорівнює см2, 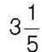А одна із сторін – см.

435°. Знайдіть сторону прямокутника, якщо його площа дорівнює 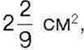а одна із сторін –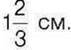

436°. Накресліть координатний промінь (одиничний відрізок – 5 клітинок зошита). Позначте на цьому промені точку 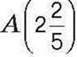. Поділіть відрізок ОА на чотири рівні частини та позначте відповідні точки. Запишіть їх координати.

437°. Накресліть координатний промінь (одиничний відрізок – 7 клітинок зошита). Позначте на цьому промені точку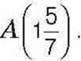

Поділіть відрізок ОА на три рівні частини та позначте відповідні точки. Запишіть їх координати.

438°. Відомо, що 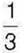деякого числа дорівнює 2. Чи правильно, що шукане число дорівнює:

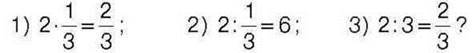
439°. Знайдіть число, якщо:

1)його 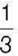дорівнює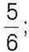

2) його 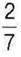дорівнюють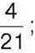

3) його дорівнюють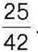

440°. Чому дорівнює довжина відрізка АВ, якщо:

1) 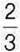його довжини дорівнюють 18 см;

2) 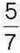його довжини дорівнюють 35 см?

441°. Чому дорівнює кут, якщо:

1) його 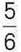дорівнюють прямому куту;

2) його 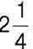дорівнюють розгорнутому куту?

442°. Чому дорівнює кут, якщо:

1) його 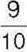дорівнюють прямому куту;

2) його 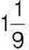дорівнює розгорнутому куту?

443. Обчисліть:

444. Обчисліть:

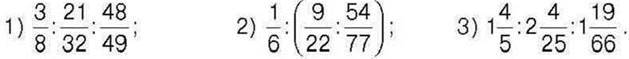
445. Знайдіть значення виразу:

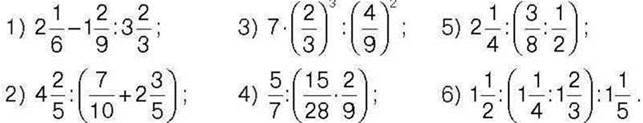
446. Обчисліть:

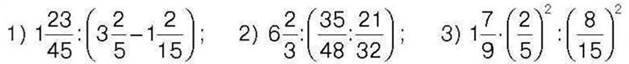
447. Площа прямокутника дорівнює 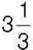см2. Знайдіть периметр прямокутника, якщо одна з його сторін дорівнює 5 см.

448. Периметр прямокутника дорівнює 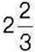см. Знайдіть площу прямокутника, якщо одна з його сторін дорівнює 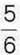см.

449. Перша сторона прямокутника дорівнює 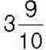см, а друга – у 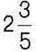раза менша, ніж перша. Знайдіть периметр та площу прямокутника.

450. Перша сторона трикутника дорівнює 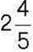м, друга – в 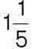раза менша від першої, а третя – в 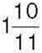раза менша від другої. Знайдіть периметр трикутника.

451. Перший спортсмен пробігає п’ять кіл на стадіоні за 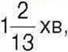а другий – сім кіл за 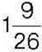хв. Який час витратить кожний із спортсменів, щоб пробігти 13 таких кіл?

452. Сергійко за перший день прочитав 90 сторінок книжки. Це становить 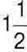того, що хлопчик прочитав за другий день, і 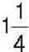того, що він прочитав за третій день. Скільки сторінок прочитав хлопчик за три дні разом?

453. Турист за перший день пройшов 18 км. Це становить 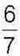шляху, який він пройшов за другий день і 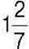шляху, який він пройшов за третій день. Який шлях пройшов турист за три дні разом? 454*. Знайдіть значення виразу:

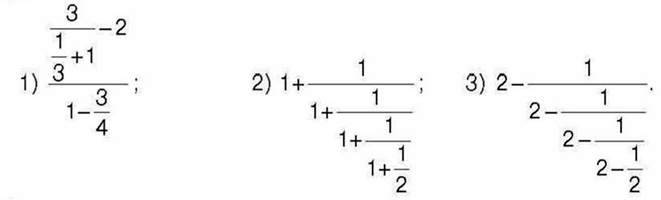
455*. Розв’яжіть рівняння:

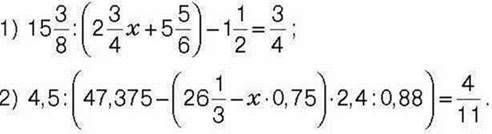
456*. Мати поділила 72 горіхи між своїми дітьми так, що середній син отримав того, що отримав молодший, а старший – того, що отримав середній. Скільки горіхів отримав кожний син?

457*. Задача Бехаєддина. Якщо число збільшити на дві третини від самого себе та ще на одиницю, то отримають 11. Знайдіть це число.

458*. Задача Бхаскари. Якщо деяке число помножити на 5, від добутку відняти його третину, остачу поділити на 10 і додати до

Цього послідовно 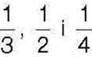початкового числа, то отримаємо 68. Яке число було спочатку?

459*. Стародавня задача. Селянин за перший день продав половину привезених гусаків та ще півгусака, за другий день –

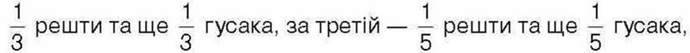а за четвертин – останніх 19 гусаків. Скільки гусаків було в селянина?

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

460. За нормами освітлення кімнати площа вікон має становити не менше 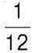площі підлоги. Чи достатньо світла в кімнаті, якщо в ній є два вікна прямокутної форми з розмірами 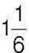м і 2 м, а підлога прямокутної форми має розміри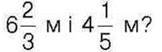

461. Одна стіна кімнати має прямокутну форму з розмірами 6,6 м і 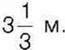Скільки рулонів шпалер потрібно купити, щоб обклеїти

Таку стіну, якщо ширина шпалер – 53 см, а довжина одного рулону -10м?

462. Для приготування фруктового салату мамі треба взятии 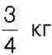бананів, що становить 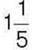маси яблук та 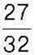маси ківі. Скільки яблук і ківі потрібно для приготування салату?

ЗАДАЧІ НА ПОВТОРЕННЯ

463. Чи існує трикутник, у якого кути дорівнюють:

1) 90°, 80°, 70°; 2) 75°, 70°, 45°; 3) 60°, 70°, 80°?

464. Щоб пропливти від одного причалу до іншого, човну потрібно 1,2 год, а щоб повернутися назад – 2 год. Власна швидкість човна дорівнює 11,2 км/год, а швидкість течії річки становить 25 % швидкості човна. Яка відстань між причалами?