Додавання і віднімання дробів з однаковими знаменниками
Урок № 5
Тема. Додавання і віднімання дробів з однаковими знаменниками
Мета. Поглибити знання учнів про дріб; вчити додавати й віднімати дроби з однаковими знаменниками. Розвивати обчислювальні навички, культуру математичної мови і записів. Виховувати самостійність, інтерес до математики.
Тип уроку: засвоєння нових знань.
Обладнання: картки з числами, таблиці: “Додавання дробів з однаковими знаменниками”, “Віднімання дробів з однаковими знаменниками”.
Хід уроку
І. Організаційний момент.
ІІ. Перевірка
1. Учні-консультанти після перевірки домашнього завдання звітуються про стан його виконання.
2. “Мікрофон”.
А) Назвати правильні дроби із знаменником 9;
Б) Назвати неправильні дроби із знаменником 9;
В) Який з дробів більший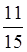 
чи 
?
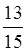Г) Який з дробів менши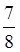й 
чи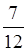 
?
ІІІ. Актуалізація опорних знань.
Усний рахунок:
1. Знайти суму чисел 275 і 34.
2. Знайти різницю чисел 156 і 45.
3. Від суми чисел 34 і 165 відняти 56.
4. До різниці чисел 89 і 45 додати 96.
Гра “Розпізнай дії”
Учитель
Таблиця № 1 “Розпізнай дії”
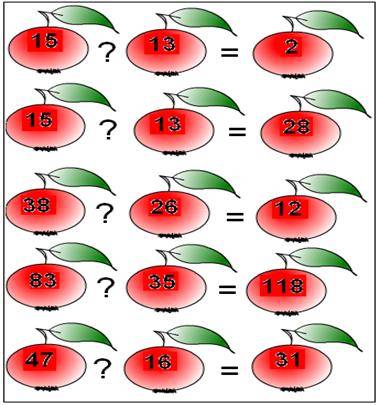
ІV. Формування нових знань.
Учитель звертає увагу учнів на таблицю.
Таблиця 2. “Додавання дробів з однаковими знаменниками”
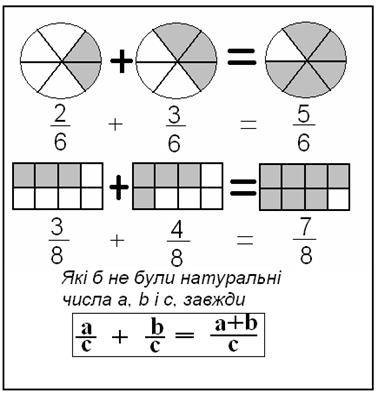
Підвести учнів до самостійного висновку щодо додавання дробів з однаковими знаменниками. Якщо перший дріб записати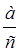 
, а другий – 
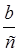, то матимемо суму: +=
.
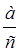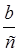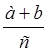Наприклад,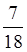 
+
=
=
.
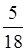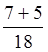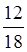Далі пропоную учням розглянути слідуючу таблицю
Таблиця 3. “Віднімання дробів з однаковими знаменниками”
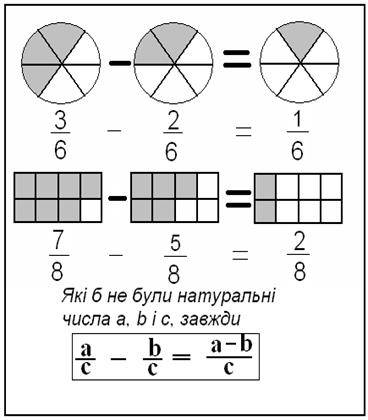
Наприклад,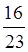 
–
=
=
.
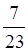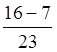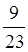Звертаю увагу учнів, що віднімання можливе лише при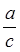 
> 
.
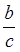Оскільки однакові знаменники прошу учнів порівняти числа.
Висновок записуємо разом, що а > b.
Далі пропоную учням додати до одного яблука його половину, третю частину, четверту.
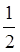1+
=1;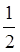 
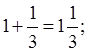
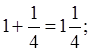
Вчу дітей як читати такі числа. Звертаю увагу дітей на назву, що це мішані числа.
Кожне мішане число має цілу і дробову частини. Дробова частина – дріб правильний.
У наведеному прикладі ціла частина – число 2, а дробова –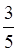 
. Оскільки 2=
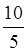, то 2=+=
.
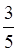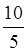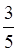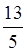Кожне мішане число дорівнює деякому неправильному дробу з тим самим знаменником. Щоб знайти чисельник цього дробу, треба цілу частину мішаного числа помножити на його знаменник і до результату додати чисельник дробової частини.
Наприклад, щоб перетворити на неправильний дріб мішане число 3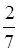
, пишемо: 3 = 
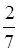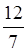. Усно знаходимо: 3ּ7 + 2 = 23. Отже, 3 = 
.
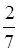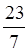Кожний неправильний дріб дорівнює або натуральному, або мішаному числу. Якщо чисельник неправильного дробу ділиться без остачі на знаменник, то цей дріб дорівнює їх частці.
Наприклад,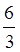 
=2, бо 6 : 3=2; 
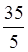=7, бо 35 : 5=7.
Якщо ж при діленні чисельника на знаменник неправильного дробу утворюються неповна частка і остача, то неповна частка – це ціла частина мішаного числа, а остача – чисельник його дробової частини. Наприклад,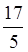 
=3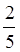
, оскільки 17 : 5 = 3 (ост. 2).
Фізкультхвилинка
Всі підняли руки – раз!
На пальчиках стоїть весь клас,
Два – присіли, руки вниз,
На сусіда подивись.
Раз! – і вгору,
Два! – і вниз,
На сусіда не дивись.
Будем дружно ми стрибати,
Щоб ногам роботу дати.
V. Формування вмінь
1. Виконаємо разом. Усний рахунок. № 1001.
2. Робота по рівнях.
І рівень № 1007.
ІІ рівень № 1008.
ІІІ рівень № 1010, № 1011.
ІV рівень № 1013, № 1014, № 1015, № 1016, № 1053.
Учні І і ІІ рівня беруть консультацію в учителя та в учнів ІV рівня. Учні ІІІ і ІV рівня консультуються між собою та з учителем.
ІV. Підсумок уроку
Історична довідка.
VІІ. Домашнє завдання
§ 22; І рівень № 1006, ІІ рівень № 1009, ІІІ рівень № 1012, VІ рівень № 1017.
(1 votes, average: 5.00 out of 5)
Loading...