ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ З ОДНАКОВИМИ ЗНАМЕННИКАМИ
РОЗДІЛ 6 ДІЇ ПЕРШОГО СТУПЕНЯ ЗІ ЗВИЧАЙНИМИ ДРОБАМИ З ОДНАКОВИМИ ЗНАМЕННИКАМИ
У розділі дізнаєтесь:
Як додавати і віднімати дроби з однаковими знаменниками;
Що таке доповнення правильного дробу до одиниці;
Як віднімати правильний дріб від натурального числа;
Які правила додавання і віднімання мішаних чисел;
Як застосувати вивчений матеріал на практиці
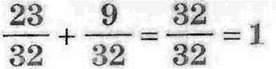
§ 26. ДОДАВАННЯ І ВІДНІМАННЯ ДРОБІВ З ОДНАКОВИМИ ЗНАМЕННИКАМИ
Ви вже знаєте, як додавати і віднімати натуральні
Так само, як і при додаванні натуральних чисел, дроби, які додають, називаються доданками, а результат додавання називається сумою.
? За яким правилом додають дроби з однаковими знаменниками? Розглянемо приклад.
Задача 1 . Мама купила дітям молочний шоколад, в якому 18 часточок. Тетянка сказала, що з’їла б 5 часточок шоколадки, а Іванко сказав, що з’їв би 7 часточок шоколадки (мал. 214). Яку частину шоколадки з’їли б Тетянка та Іванко разом?
Мал. 214
Розв’язання. Одна часточка становить
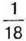частину шоколадки. Тоді Тетянка з’їла 6 
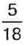шоколадки, а Іванко – 
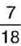шоколадки. Разом діти з’їли б 12 часточок, тобто 
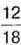шоколадки.Розв’язуючи задачу, ми діяли, як з іменованими числами – додавали кількість часточок шоколадки, а словом “часточка” називали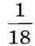 
частину шоколадки.
Іншими словами, шукаючи суму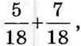 
ми залишили без змін однаковий знаменник доданків, а додали лише їх чисельники. Спробуйте самостійно сформулювати правило додавання дробів з однаковими знаменниками та порівняйте його з наведеним у підручнику.
Правило додавання дробів з однаковими знаменниками.
Щоб знайти суму двох дробів з однаковими знаменниками, треба:
1) спільний знаменник записати в знаменнику суми;
2) додати чисельники і результат записати в чисельнику суми.
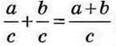
Наприклад:
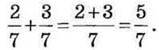
? Чи зберігається правило додавання для трьох і більше дробів з однаковими знаменниками? Так. Наприклад:
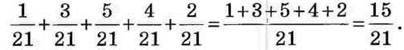
При додаванні дробів, так само, як і при додаванні натуральних чисел, виконуються закони додавання.
Задача 2. Знайдіть суму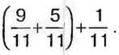 
Розв’язання.
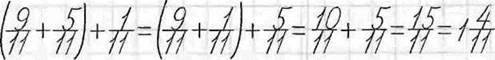
Зверніть увагу:
Якщо при додаванні дробів з однаковими знаменниками в результаті отримали неправильний дріб, то в ньому треба виділити цілу й дробову частини і подати відповідь мішаним числом.
Задача 3. Мама дала дітям 11 часточок молочного шоколаду, всього їх було 18. Тетянка з’їла 4 часточки шоколадки, а іншу частину з’їв Іванко. На яку частину шоколадки більше з’їв Іванко, ніж Тетянка?
Розв’язання. Одна часточка становить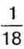 
частину шоколадки. Тетянка з’їла 
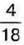шоколадки, з’їв Іванко з’їв 11 – 4 = 7 часточок, тобто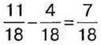 
Шоколадки. Для того щоб знайти, на скільки більше з’їв Іванко, ніж Тетянка, треба від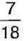 
відняти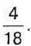 
Матимемо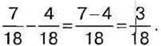 
Відповідь: Іванко з’їв більше, ніж Тетянка на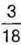 
шоколадки.
Правило віднімання дробів з однаковими знаменниками.
Щоб знайти різницю двох дробів з однаковими знаменниками, треба:
1) спільний знаменник записати в знаменнику різниці;
2) від чисельника зменшуваного відняти чисельник від’ємника і результат записати в чисельнику різниці.
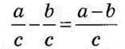
Зверніть увагу:
Різниця двох дробів з однаковими знаменниками, в яких чисельники рівні, завжди дорівнює нулю.
У Стародавньому Римі були поширені так звані дванадцяткові дроби. Мідну монету, а пізніше одиницю ваги, римляни ділили на дванадцять рівних частин – унцій. У школах Стародавнього Риму обчисленням з дробами приділялась особлива увага. У книзі “Наука поезії” Горацій наводить наступний діалог учителя і учня.
– Син Альбіна! Скажи мені: якщо ми, взявши п’ять унцій, віднімемо одну, що залишиться? – запитав учитель,
– Третина асса, – відповів учень.
– Прекрасно! А якщо ми додамо до попередніх п’яти унцій ще одну, скільки вийде всього? – знову запитує вчитель.
– Пів-асса, – відповідає учень.
Перекладемо цю задачу сучасною мовою. Врахуємо, що:
1 асс = 12 унцій (приблизно 327 г).
Тоді:
Мал. 215
1012. Потрібно додати два дроби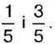 
1) Яким буде знаменник отриманого в сумі дробу:
А) 5; 6)10; в) 25; г)4?
2) Яким буде чисельник отриманого в сумі дробу:
А) 5; 6)4; в) 3; г) 10?
3) Назвіть дріб, який є результатом додавання даних дробів.
1013. Якщо до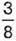 
додати 
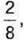то в результаті отримаємо дріб, у якого:
1) чисельник дорівнює: а) 1; б) 2; в) 5; г) 8;
2) знаменник дорівнює: а) 5; б) 8; в) 16; г) 64.
1014. Чи правильно, що сумою дробів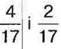 
є дріб:
1015. Потрібно відняти два дроби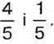 
1) Яким буде знаменник отриманого в результаті віднімання дробу: а) 5; б) 10; в) 25; г) З?
2) Яким буде чисельник отриманого в результаті віднімання дробу: а) 5; 6)4; в) 3; г) 10?
3) Назвіть дріб, який є результатом віднімання даних дробів.
1016. Якщо від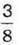 
Відняти 
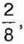то в результаті отримаємо дріб, у якого:
1) знаменник дорівнює: а) 1; б) 8; в) 0; г) 16;
2) чисельник дорівнює: а) 8; б) 6; в) 5; г) 1.
1017. Чи правильно, що різницею дробів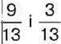 
є дріб:
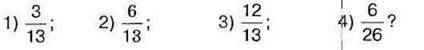
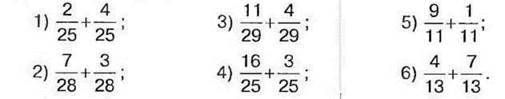
1019. Знайдіть суму дробів:
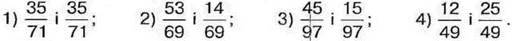
1020. Обчисліть:
1021. Обчисліть:
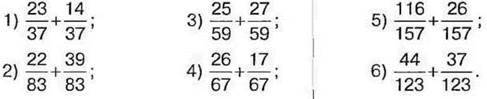
1022. Знайдіть значення суми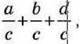 
якщо:
1) а= 1, b = 2, с = 5, d= 1;
2) а = 2, b = 5, с=11,d = 3;
3) а = 7, b = 6, с = 23, d = 5.
1023. Знайдіть суму:
1) двох сьомих і трьох сьомих;
2) сімнадцяти двадцять сьомих і п’яти двадцять сьомих;
3) дев’яти двадцять других і п’яти двадцять других.
1024. Порівняйте:
1025. Порівняйте:
1026. Додайте дроби:
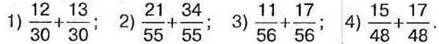
1027. Додайте дроби:
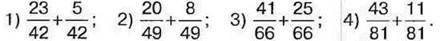
1028. Знайдіть зменшуване, якщо різниця дорівнює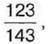 
а від’ємник –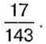 
1029. Розв’яжіть рівняння:
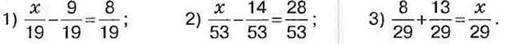
1330. Розв’яжіть рівняння:
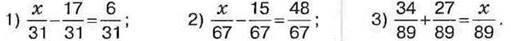
1031. Щоб пришити гудзики до плаття, Оксанка витратила 15 хв, а щоб випрасувати плаття – 10 хв. Яку частину години витратила дівчинка для приведення свого плаття в порядок?
1032. На уроці математики діти писали контрольну роботу.
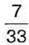усіх учнів отримали оцінки від 10 до 12 балів, 
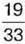– від 7 до 9 балів, решта учнів – оцінки, нижчі від 6 балів. Яка частина учнів отримала хороші оцінки (від 7 до 12 балів)?
1033.Обчисліть усно:
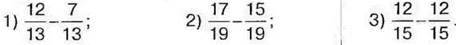
1034. Знайдіть різницю дробів:
1035. Обчисліть:
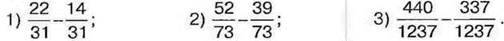
1036. Знайдіть значення різниці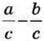 
Якщо:
1) а=6, b = 3, с = 7; 2)а = 8, b=5, с=11.
1037. Знайдіть різницю дробів:
1) тринадцять п’ятнадцятих і сім п’ятнадцятих;
2) тридцять чотири сорок перших і тринадцять сорок перших;
3) п’ятдесят вісім дев’яносто дев’ятих і одинадцять дев’яносто дев’ятих.
1038. Відніміть дроби:
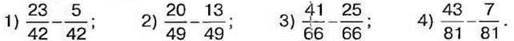
1039. Сума трьох дробів дорівнює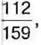 
два із цих дробів дорівнюють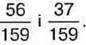 
Знайдіть невідомий дріб.
1040. Сума двох дробів дорівнює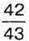 
а один із дробів –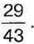 
Знайдіть інший дріб.
1041. Які числа потрібно підставити замість букв а або b, щоб рівність була правильною:
1042. Розв’яжіть рівняння:
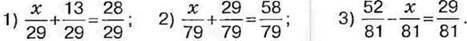
1043. Розв’яжіть рівняння:
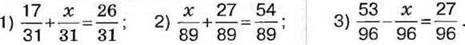
1044.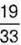 
дівчаток 5-Б класу відвідує спортивні секції, причому 
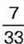займається волейболом, а інша частина – гімнастикою.
Яка частина дівчаток класу займається гімнастикою?
1045. У магазин завезли партію овочів.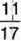 
усіх овочів складає перець, а 
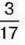– огірки. На скільки більше завезли до магазину перцю, ніж огірків?
1046. Обчисліть:
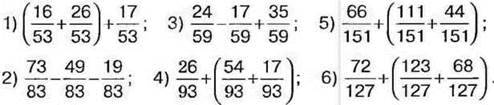
1047. Обчисліть:
1048. Розмістіть наступні суми у порядку зростання їх значень:
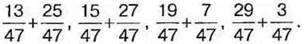
1049. Розмістіть наступні різниці у порядку спадання їх значень:
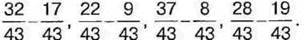
1050. Знайдіть значення виразу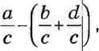 
якщо:
1) а = 51, b = 23, с = 77, d= 14;
2) а = 72, b = 25, c = 97,d = 33;
3) а= 107, b = 26, с= 127, d = 66.
1051. Розв’яжіть рівняння:
1052. Розв’яжіть рівняння:
1053. Відрізок АВ завдовжки 26 см поділено на частини точками М і N. Відрізок AM становить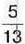 
відрізка АВ, а відрізок MN – 
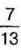відрізка АВ. Яка довжина відрізка NB?
1054. Відрізок MN завдовжки 48 см поділено на частини точками А і С. Відрізок МА становить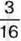 
відрізка MN, відрізок АС – 
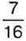відрізка MN. Яка довжина, відрізка CN?
1055. У мікрорайоні проживає 6300 дітей шкільного віку. У першій школі навчається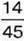 
усіх учнів, у другій школі – на 
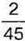учнів більше, ніж у першій, а в третій школі – на 
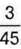менше, ніж у другій. Решта дітей навчається в школах іншого мікрорайону. Яка частина дітей навчається у трьох школах разом? Скільки дітей навчається у трьох школах разом? Скільки дітей навчається в інших школах?
1056. У конкурсі “Кенгуру” в 2010 р. взяли участь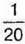 
учнів школи, у 2011р. – 
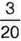учнів школи, а в 2012 р. – на 
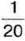більше від суми частин учнів за два попередні роки. Яка частина учнів взяла участь у конкурсі “Кенгуру” за три роки? Скільки учнів взяли участь у конкурсі за три роки разом, якщо у школі навчається 600 учнів?
1057. Марійка задумала деякий дріб, який спочатку збільшила на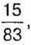 
а потім – ще на 
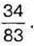У результаті вона отримала 
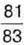Яке число задумала Марійка?
1058. Андрій задумав деякий дріб, який спочатку збільшив на 
А потім зменшив на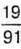 
. У результаті він отримав 
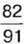, Яке число задумав Андрій?
1059. На скільки сума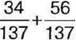 
менша від числа 
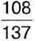і більша за різницю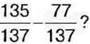 
1060. На скільки сума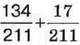 
більша за різницю 
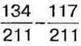і менша від суми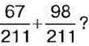 
1061. Обчисліть:
1062. Послідовно записано кілька чисел. Перше число дорівнює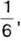 
а кожне наступне – на 
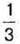більше за попереднє.
1063. Знайдіть суму чисел:
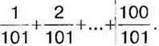
1064. Запишіть дріб, знаменник якого є найбільшим чотирицифровим числом, а чисельник дорівнює сумі всіх трицифрових чисел, кожне з яких записане одними і тими ж цифрами.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
1065. Відстань від Києва до Харкова становить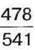 
відстані від Києва до Львова, а відстань від Києва до Черкас – на 
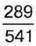менша. Яку частину відстані від Києва до Львова становить відстань від Києва до Черкас? Яка відстань від Києва до Черкас та від Києва до Харкова, якщо відстань від Києва до Львова дорівнює 541 км?
1066. Як поділити 7 хлібин на 8 осіб?
1067. Марина допомагала мамі по господарству.
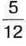год вона прибирала в кімнаті. Знайдіть число, яке стоїть на п’ятому місці в цій послідовності.
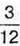год – мила посіуд. Скільки часу Марина займалася домашнім господарством?
ЗАДАЧА НА ПОВТОРЕННЯ
1068. Обчисліть:
1) 11120 + 5555 + 21080 + 4445; 2) 8 год 37 хв – 6 год 56 хв.
1069. Відстань між двома містами 60 км. З них одночасно виїхали в одному напрямку два велосипедисти. Швидкість одного з них 12 км/год, а іншого, що ще слідом за першим, – 15 км/год. Через який час другий велосипедист наздожене першого?
1070. Розв’яжіть рівняння:
1) (140-х)∙15=1845; 2) 325-(х-340): 9 = 85.
1071. Іринка прочитала 60 сторінок “Тореадорів з Васюківки” за 2 год, а Олег – за 3 год. Скільки часу потрібно кожному з дітей, щоб прочитати книгу повністю якщо в ній 540 сторінок?
(1 votes, average: 5.00 out of 5)
Loading...