Головна ⇒ 📌Довідник з геометрії ⇒ Доведення від супротивного
Доведення від супротивного
Геометрія
Основні властивості найпростіших геометричних фігур
Доведення від супротивного
Цей спосіб доведення складається з таких етапів.
1. Припускають протилежне тому, що стверджується теоремою.
2. На основі припущення, спираючись на аксіоми і вже доведені теореми, роблять висновки.
3. Знаходять, у чому цей висновок суперечить умові, якійсь аксіомі або доведеній раніше теоремі.
4. Роблять висновок, що зроблене припущення неправильне, а тому правильне твердження теореми.
Особливо часто використовують цей спосіб
Приклад. Довести, що в трикутнику може бути тільки один тупий кут.
Доведення:
1) Припустимо, що в трикутнику є два тупих кути.
2) Тоді сума кутів трикутника більша за
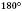 , тому що міра тупого кута більша за
, тому що міра тупого кута більша за 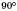 .
.3) Зроблений висновок суперечить теоремі про суму кутів трикутника.
4) Отже, наше припущення неправильне, а правильне те, що треба було довести.
Related posts:
- Розв’язування задач на застосування теореми синусів УРОК № 8 Тема. Розв’язування задач на застосування теореми синусів Мета уроку: формування вмінь учнів застосовувати теорему синусів до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13], посібник [14]. Вимоги до рівня підготовки учнів: застосовують теорему синусів до розв’язування задач. Хід уроку І. Перевірка домашнього завдання 1. […]...
- Сума кутів трикутника Геометрія Основні властивості найпростіших геометричних фігур Сума кутів трикутника Теорема. Сума кутів трикутника дорівнює . Із цієї теореми випливають наслідки: 1. У будь-якому трикутнику принаймні два кути гострі (тобто в трикутнику не може бути більше одного прямого або тупого кута). 2. Кути рівностороннього трикутника дорівнюють . Зовнішнім кутом трикутника при даній вершині називається кут, суміжний […]...
- Теорема синусів Геометрія Розв’язування трикутників Теорема синусів Теорема 1 (синусів). Сторони трикутника пропорційні до синусів протилежних кутів. У трикутнику, зображеному на рисунку, за теоремою синусів маємо: . Теорема 2. Якщо R – радіус кола, описаного навколо трикутника, то , або , де a – сторона трикутника, а – протилежний цій стороні кут. Теорема 3. У трикутнику проти […]...
- Властивості кутів трикутника Розділ 1. Найпростіші геометричні фігури та їх властивості § 10. Властивості кутів трикутника 344. ∠E = 60°, ∠F = 40°, ∠D = 80°. ∠E + ∠F + ∠D = 60° + 40° + 80° = 180°. 345. На мал. 208 неправильно сказано градусну міру кутів? АВС, оскільки? ABC – прямокутний, a ∠B + ∠C = […]...
- Рівнобедрений трикутник Урок № 23 Тема. Рівнобедрений трикутник Мета: домогтися свідомого розуміння учнями понять: – умова та висновок теореми; – пряма та обернена теореми; – формулювання та доведення ознаки рівнобедреного трикутника. Сформувати вміння: – відтворювати теорему – ознаку рівнобедреного трикутника; – виділяти у формулюванні теореми умову та висновки; – використовуючи знання про пряму та обернену теореми, складати […]...
- Пряма й обернена теореми Геометрія Основні властивості найпростіших геометричних фігур Пряма й обернена теореми Формулювання теореми складається з двох частин. В одній говориться про те, що дано. Ця частина називається Умовою. У другій частині говориться про те, що треба довести. Ця частина називається Висновком. Приклади 1) Якщо кути суміжні, то їх сума дорівнює 180°. Умова Висновок 2) У прямокутному […]...
- НЕРІВНОСТІ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 15. НЕРІВНОСТІ ТРИКУТНИКА Ви вже знаєте, що кожна сторона трикутника менша від суми двох інших його сторін. Щоб довести це твердження як теорему, спочатку розглянемо іншу теорему. Теорема 19 У кожному трикутнику проти більшої сторони лежить більший кут, а проти більшого кута – більша сторона. Доведення. 1) Нехай у трикутнику ABC […]...
- Теорема косинусів Геометрія Розв’язування трикутників Теорема косинусів Теорема (косинусів). Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін і косинуса кута між ними. У трикутнику, зображеному на рисунку, за теоремою косинусів: . Теорему косинусів зручно застосувати для розв’язування таких задач. 1. Знайти сторону трикутника, якщо відомі дві інші сторони й кут […]...
- Числові нерівності. Доведення числових нерівностей УРОК № 2 Тема. Числові нерівності. Доведення числових нерівностей Мета уроку: домогтися засвоєння учнями змісту: додаткових нерівностей для суми взаємно обернених додатних чисел та середнього арифметичного двох невід’ємних чисел (у порівнянні з їх середнім геометричним) та доведення цих нерівностей; способу застосування доведених нерівностей при доведенні інших числових нерівностей. Продовжити роботу з вироблення вмінь: відтворювати зміст […]...
- Тотожні вирази, тотожність. Тотожне перетворення виразу. Доведення тотожностей Розділ 1. ЦІЛІ ВИРАЗИ & 2. Тотожні вирази, тотожність. Тотожне перетворення виразу. Доведення тотожностей Знайдемо значення виразів 2(х – 1) і 2х – 2 для деяких даних значень змінної х. Результати запишемо в таблицю: Х -4 -3 -2 -1 0 1 2 3 4 2(х – 1) -10 -8 -6 -4 -2 0 2 4 […]...
- Порівняння сторін і кутів трикутника Урок № 37 Тема. Порівняння сторін і кутів трикутника Мета: перевірити рівень засвоєння навчального матеріалу теми “Прямокутні трикутники”; домогтися засвоєння учнями змісту та схеми доведення теореми про співвідношення між сторонами і кутами трикутника; сформувати вміння відтворювати формулювання теореми про співвідношення між сторонами і кутами трикутника та використовувати це співвідношення під час розв’язування задач. Тип уроку: […]...
- Теорема косинусів УРОК № 4 Тема. Теорема косинусів Мета уроку: вивчення теореми косинусів. Формування вмінь учнів застосовувати теорему косинусів до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника”[13]. Вимоги до рівня підготовки учнів: формулюють теорему косинусів та доводять її. Хід уроку I. Перевірка домашнього завдання Перевірити наявність виконаних домашніх завдань […]...
- Теорема синусів УРОК № 7 Тема. Теорема синусів Мета уроку: вивчення теореми синусів. Формування вмінь учнів застосовувати вивчену теорему до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Співвідношення між сторонами і кутами трикутника” [13]. Вимоги до рівня підготовки учнів: формулюють теорему синусів та доводять її. Хід уроку І. Перевірка домашнього завдання Перевірити правильність виконання домашніх […]...
- Суміжні та вертикальні кути § 1. Найпростіші геометричні фігури та їхні властивості § 4. Суміжні та вертикальні кути Практичні завдання 86. ∠BAC – гострий, ∠OAB – суміжний до кута ВАС. ∠АОВ – прямий, ∠COA – суміжний до кута АОВ. ∠BOC – тупий, ∠AOB – суміжний до кута ВОС. 87. ∠AOC і ∠COB – суміжні. 88. а) ∠ABD i ∠CBD; […]...
- Нерівність трикутника Урок № 38 Тема. Нерівність трикутника Мета: домогтися засвоєння змісту теореми, що виражає нерівність трикутника та схему її доведення та наслідку з теореми; виробляти вміння відтворювати формулювання доведених на уроці тверджень та застосувати для розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Нерівність трикутників та наслідки […]...
- Площа ортогональної проекції многокутника Урок 56 Тема. Площа ортогональної проекції многокутника Мета уроку: вивчення теореми про площу ортогональної проекції многокутника, формування вмінь учнів застосовувати вивчену теорему до розв’язування задач. Обладнання: стереометричний набір, модель куба. Хід уроку 1. Два учні відтворюють розв’язування задач № 42, 45 на дошці. 2. Фронтальне опитування. 1) Дайте означення кута між двома площинами, які перетинаються. […]...
- СУМА КУТІВ ТРИКУТНИКА РОЗДІЛ 3 ТРИКУТНИКИ & 10. СУМА КУТІВ ТРИКУТНИКА Теорема 8 Сума кутів трикутника дорівняй: 180°. Доведення. Нехай ABC – довільний трикутник (мал. 130). Через йот вершину С проведемо пряму КР, паралельну стороні АВ. Утворені кути АСК і ВСР позначимо цифрами 1 і 2. Тоді ∠A = ∠1, ∠B = ∠2, як внутрішні різносторонні кути при […]...
- Прямокутний трикутник Урок № 36 Тема. Прямокутний трикутник Мета: домогтися засвоєння учнями властивості прямокутного трикутника з гострим кутом 30° та оберненого твердження і схеми їх доведень; сформувати в учнів уміння відтворювати формулювання цих тверджень та використовувати їх для розв’язування задач; удосконалювати вміння використовувати набуті раніше знання для розв’язування задач на прямокутний трикутник. Тип уроку: засвоєння знань, умінь […]...
- Теореми § 2. Трикутники 11. Теореми 269. Теорема Умова Висновок 4.1 Кути АОС і СОВ – суміжні ∠AOC + ∠COB = 180° 8.2 X належить серединному перпендикуляру відрізка AB ХА = ХВ 9.1 ?ABC – рівнобедрений з основою АС 1) ∠A = ∠C; 2) бісектриса кута В є медіаною і висотою 10.3 Два кути трикутника ABC […]...
- Теореми про рівність і подібність трикутників – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Трикутник – де багатокутник із трьома сторонами. Сторони трикутника позначаються малими буквами, що відповідають позначенню протилежних вершин. Якщо всі три кути гострі – трикутник гострокутний. Якщо один з кутів прямий – прямокутний; сторони, що утворюють прямий кут, називаються катетами (а і b), сторона проти прямого кута – гіпотенузою (с). Якщо […]...
- ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ РОЗДІЛ 2 ВЗАЄМНЕ РОЗТАШУВАННЯ ПРЯМИХ НА ПЛОЩИНІ & 6. ОЗНАКИ ПАРАЛЕЛЬНОСТІ ПРЯМИХ Важливу роль у дослідженні паралельності прямих відіграють поняття січної та деяких пар кутів. Нехай а і b – дві довільні прямі площини. Пряму с, що їх перетинає, називають січною прямих а і b (мал. 73). Прямі а і b з їх січною с […]...
- Сума кутів трикутника Урок № 34 Тема. Сума кутів трикутника Мета: закріпити знання учнів про зміст теореми про суму кутів трикутника та наслідків з неї; працювати над засвоєнням поняття “зовнішній кут трикутника”; розглянути властивість зовнішнього кута трикутника. Сформувати вміння: – знаходити на рисунку та виконувати зображення зовнішнього кута при даній вершині трикутника; – записувати теорему про зовнішній кут […]...
- Властивість медіани, бісектриси й висоти рівнобедреного трикутника Урок № 25 Тема. Властивість медіани, бісектриси й висоти рівнобедреного трикутника Мета: домогтися свідомого сприйняття учнями змісту теореми про властивість медіани, бісектриси й висоти рівнобедреного трикутника та наслідків з неї; сформувати вміння відтворювати названі властивості та застосовувати їх під час розв’язування задач. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського […]...
- Перша ознака рівності трикутників Урок № 18 Тема. Перша ознака рівності трикутників Мета: закріпити знання учнями формулювання першої ознаки Рівності трикутників та алгоритму її застосування; формувати навички застосування теореми для розв’язування задач. Тип уроку: засвоєння вмінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Ознаки рівності трикутників”. ХІД УРОКУ I. Організаційний момент II. Перевірка домашнього завдання Математичний […]...
- Висота, бісектриса, медіана трикутника Геометрія Основні властивості найпростіших геометричних фігур Висота, бісектриса, медіана трикутника Висотою Трикутника, опущеною з даної вершини, називається перпендикуляр, проведений із цієї вершини до прямої, що містить протилежну сторону трикутника. У кожному трикутнику можна провести три висоти. Висоти трикутника (або прямі, що їх містять) перетинаються в одній точці. На рисунках зображено, як перетинаються висоти в гострокутному […]...
- Застосування подібності: властивість бісектриси трикутника Урок № 37 Тема. Застосування подібності: властивість бісектриси трикутника Мета: домогтися засвоєння учнями змісту теореми, що виражає властивість бісектриси трикутника та її доведення. Формувати вміння: – відтворювати зміст вивченої теореми; – за готовими рисунками із зображенням трикутника та його бісектриси знаходити пропорційні відрізки; – виконувати записи відповідно до формулювання теореми та умови задачі; – застосовувати […]...
- Рівносторонній трикутник – ТРИКУТНИКИ Формули й таблиці МАТЕМАТИКА ТРИКУТНИКИ Рівносторонній трикутник Усі висоти, медіани й бісектриси мають однакову довжину. Вписане і описане коло мають спільний центр. Середня лінія трикутника – відрізок, що сполучає середини двох сторін трикутника. Теорема: Зовнішній кут трикутника – кут, суміжний із внутрішнім кутом трикутника. Теорема: Теорема косинусів: у будь-якому трикутнику зі сторонами а, b, с […]...
- Зовнішній кут трикутника та його властивості Розділ 3. Трикутники. Ознаки рівності трикутників § 18. Зовнішній кут трикутника та його властивості 438. ∠BAK – зовнішній кут при вершині А. 439. ∠LDP – зовнішній кут при вершині D. 441. ∠A + ∠B = 70° – за властивістю зовнішнього кута трикутника. 442. Зовнішній кут трикутника при вершині С дорівнює 74° згідно з властивістю зовнішнього […]...
- Середня лінія трикутника Урок № 17 Тема. Середня лінія трикутника Мета: сформувати в учнів поняття середньої лінії трикутника. Розглянути властивості середньої лінії трикутника та зміст задачі Вариньйона; формувати в учнів уміння: відтворювати вивчені твердження (означення та властивості); виконувати зображення середніх ліній трикутника та здійснювати доведення або спростування того, що даний відрізок є середньою лінією трикутника; відтворювати доведення властивості […]...
- Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Урок № 57 Тема. Формули доповнення. Значення тригонометричних функцій кутів 30°, 45°, 60° Мета: сформувати в учнів свідоме розуміння змісту та доведення теореми, що містить формули доповнення, а також наслідку з неї; домогтися засвоєння учнями способу обчислення та значень тригонометричних функцій кутів 30°, 45° і 60°. Закріпити знання вивчених формул та сформувати вміння їх застосовувати […]...