Довжина кола і дуги кола
УРОК № 20
Тема. Довжина кола і дуги кола
Мета уроку: виведення формул для знаходження довжини кола та довжини дуги кола. Формування вмінь учнів застосовувати виведені формули до розв’язування задач.
Тип уроку: комбінований.
Наочність і обладнання: таблиця “Довжина кола і площа круга” [13].
Вимоги до рівня підготовки учнів: записують і пояснюють формули довжини кола і дуги кола. Формулюють теорему про відношення довжини кола до його діаметра. Застосовують вивчені формули до розв’язування задач.
Хід уроку
І.
Перевірити наявність виконаних домашніх завдань та відповісти на запитання, які виникли в учнів при виконанні домашніх завдань.
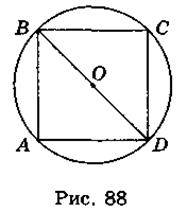
Задача 1. Розв’язання
Нехай BD = 4 см (рис. 88), тоді ОВ = 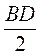 =
= 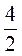 = 2 см, АВ = ОВ
= 2 см, АВ = ОВ = 2
= 2 (см).
(см).
Відповідь. 2 см.
см.
Задача 2. Доведення
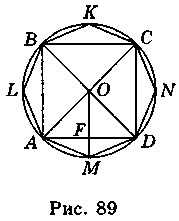
Нехай ABCD – квадрат, AMDNCKBL – правильний восьмикутник (рис. 89), точка О – центр цих многокутників, OA = R. Із прямокутного трикутника AMF маємо AM =
 = R
= R .
.FM = OM – OF = R – 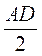 = R –
= R – 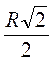 , маємо: AM =
, маємо: AM = 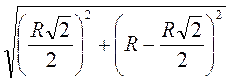 =
= 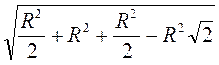 =
= 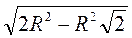 =
= 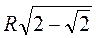 .
.
Фронтальна бесіда
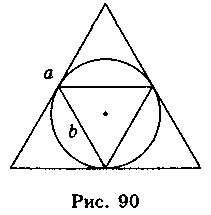
1) У коло вписано правильний трикутник, і навколо цього самого кола описано правильний трикутник (рис. 90). Сторона описаного трикутника дорівнює а, а сторона вписаного – b. Визначте, які з наведених тверджень є правильними, а які – неправильними.
А) a = 3b.
Б) Точки перетину медіан обох трикутників збігаються.
В) Радіус кола дорівнює 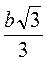 .
.
Г) Радіус кола дорівнює 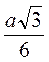 .
.
2) Навколо квадрата описано коло радіуса R, і в цей самий квадрат вписано коло радіуса r (рис. 91). Визначте, які з наведених тверджень є правильними, а які – неправильними.
А) R = r .
.
Б) Центри описаного та вписаного кіл збігаються.
В) Сторона квадрата дорівнює R .
.
Г) Сторона квадрата дорівнює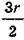
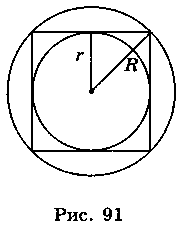
Самостійна робота
Самостійну роботу можна провести за посібником [14], тест 6 “Правильні многокутники”.
II. Первинне сприймання й усвідомлення нового матеріалу
Довжина кола
Щоб наочно уявити, що таке довжина кола, уявимо, що коло зроблено з тонкого дроту. Якщо таке коло розрізати в деякій точці А і розпрямити коло, то одержимо відрізок AA1, довжина якого і є довжиною кола (рис. 92).
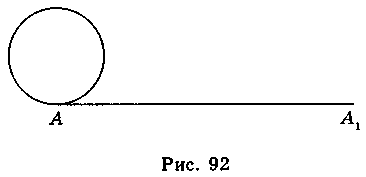
Периметр будь-якого правильного вписаного в коло многокутника є наближеним значенням довжини кола. Чим більше число сторін такого многокутника, тим точніше це наближення, оскільки многокутник при збільшенні числа сторін все ближче і ближче “прилягає” до кола.
Теорема. Відношення довжини кола до його діаметра одне й те саме для кожного кола.
Доведення
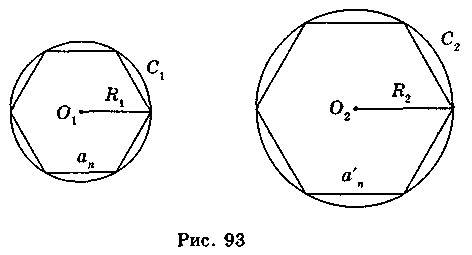
Нехай маємо два довільних кола (рис. 93), радіуси яких дорівнюють R1 і R2, а довжини кіл – С1 і С2. У кожне з цих кіл впишемо правильні n-кутники з однаковим числом сторін, довжини яких дорівнюють аn і а’n, тоді їх периметри Рn і Р’n відповідно дорівнюватимуть:
Pn = nan = n • 2R1sin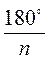 , Р’n = na’n = n • 2R2sin
, Р’n = na’n = n • 2R2sin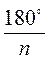 .
.
Тоді 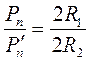 .
.
Якщо значення n необмежено збільшувати, то периметри Рn і Р’n прямуватимуть до довжин кіл С1 і С2, а відношення периметрів – до відношення 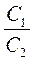 . Отже,
. Отже, 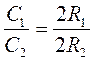 , або
, або 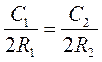 , що і треба було довести.
, що і треба було довести.
Відношення довжини кола С до його діаметра 2R прийнято позначати грецькою буквою n. Число n – ірраціональне число, його наближене значення n  3,1415926.
3,1415926.
Отже, 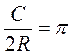 , звідки C = 2nR.
, звідки C = 2nR.
C = 2nR – формула довжини кола.
Виконання вправ
1. Знайдіть довжину кола радіуса 5 см. 2. Знайдіть довжину кола діаметра 5 см. 3. Знайдіть радіус кола, довжина якого дорівнює 16n см. 4. Знайдіть діаметр кола, довжина якого дорівнює 5n см.
Знаходження довжини дуги кола
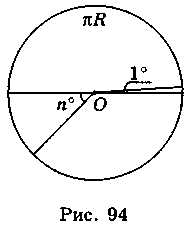
Знайдемо довжину дуги кола, яка відповідає центральному куту п°. Оскільки розгорнутому куту відповідає довжина півкола? R (рис. 94), то куту 1° відповідає дуга довжиною 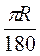 , а куту п° – дуга довжиною
, а куту п° – дуга довжиною 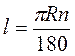 .
.
Виконання вправ
1. Знайдіть довжину дуги кола радіуса 1 см, яка відповідає центральному куту, що становить:
А) 30°; б) 270°.
Розв’язання
А) 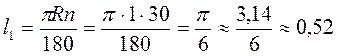 (см);
(см);
Б) 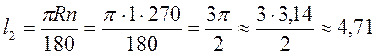 (см);
(см);
Відповідь. 0,52 см; 4,71 см.
2. Скільки градусів містить центральний кут, якщо відповідна йому дуга становить:
А)  ; б)
; б) 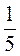 ; в)
; в) 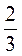 кола?
кола?
Розв’язання
 • 360° = 120°;
• 360° = 120°; 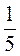 • 360° = 72°;
• 360° = 72°; 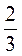 • 360° = 240°.
• 360° = 240°.
Відповідь. 120°, 72°, 240°.
3. За даним радіусом R = 1 м знайдіть довжину дуги, яка відповідає центральному куту, що становить:
А) 45°; б) 120°; в) 60°30′; г) 150°36′.
Розв’язання
А) 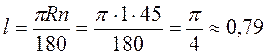 (м);
(м);
Б) 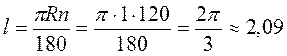 (м);
(м);
В) 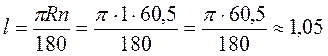 (м);
(м);
Г) 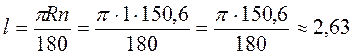 (м).
(м).
Відповідь.  0,79 м;
0,79 м;  2,09 м;
2,09 м;  1,05 м;
1,05 м;  2,63 м.
2,63 м.
III. Закріплення й осмислення нового матеріалу
Розв’язування задач
1. Довжина кола, описаного навколо квадрата, дорівнює 6? см. Знайдіть сторону цього квадрата. (Відповідь. 3 См.) 2. Сторона правильного трикутника дорівнює а. Знайдіть довжину кола, що є:
См.) 2. Сторона правильного трикутника дорівнює а. Знайдіть довжину кола, що є:
А) вписаним у цей трикутник;
Б) описаним навколо цього трикутника.
(Відповідь, а) 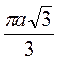 ; б)
; б) 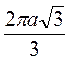 .)
.)
3. Знайдіть радіус кола, дуга якого має довжину 15,7 см і відповідає центральному куту, що становить 24°. (Відповідь.  37,5 см.) 4. Довжини основ і бічної сторони рівнобічної трапеції відповідно дорівнюють 9 см, 25 см і 17 см. Знайдіть довжину кола, вписаного в трапецію. (Відповідь. 15? см.) 5. Довжина відрізка АВ дорівнює а. На ньому позначено точки С1, С2, …, Сn і побудовано півкола (рис. 95), які мають діаметри АС1, С1С2, …, СnВ. Знайдіть довжину побудованої кривої з кінцями в точках А і В. (Відповідь.
37,5 см.) 4. Довжини основ і бічної сторони рівнобічної трапеції відповідно дорівнюють 9 см, 25 см і 17 см. Знайдіть довжину кола, вписаного в трапецію. (Відповідь. 15? см.) 5. Довжина відрізка АВ дорівнює а. На ньому позначено точки С1, С2, …, Сn і побудовано півкола (рис. 95), які мають діаметри АС1, С1С2, …, СnВ. Знайдіть довжину побудованої кривої з кінцями в точках А і В. (Відповідь. 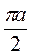 .)
.)
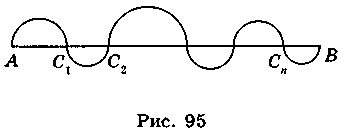
6. Знайдіть відношення периметра правильного восьмикутника до діаметра і порівняйте його з наближеним значенням n.
Розв’язання
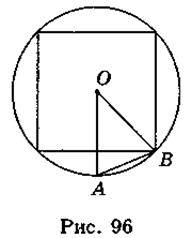
Нехай АВ – сторона восьмикутника (рис. 96), тоді за теоремою косинусів із трикутника АОВ маємо: АВ2 = ОА2 + ОВ2 – 2 • ОА • OB • cos  AOB, де OA = OB = R,
AOB, де OA = OB = R,  АОВ = 360° : 8 = 45°. Тоді AB2 = R2 + R2 – 2 • R2 •
АОВ = 360° : 8 = 45°. Тоді AB2 = R2 + R2 – 2 • R2 • 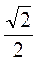 = 2R2 – R2
= 2R2 – R2 , AB =
, AB = 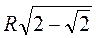 .
.
Периметр восьмикутника P8 = 8AB = 8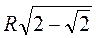 , діаметр кола 2R.
, діаметр кола 2R.
Отже, P8 : 2R = 8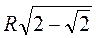 : 2R = 4
: 2R = 4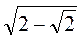
 3,06, а n
3,06, а n  3,14.
3,14.
Відповідь. 3,06 < 3,14.
7. Шків діаметра 1,4 м здійснює 80 обертів за хвилину. Знайдіть швидкість точки на ободі шківа.
Розв’язання
Довжина шківа: C = 2nR = n • 1,4 = 4,396 (м). Шлях, пройдений точкою за хвилину: S = C • 80 = 4,396 • 80 = 351,68 (м).
Швидкість точки на ободі шківа:
V = 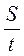 =
= 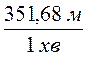 = 351,68
= 351,68 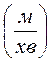 .
.
Відповідь. 351,68 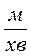 .
.
8. Відстань між якими двома точками на поверхні Землі дорівнює 1 км? Радіус Землі дорівнює 6370 км. Який кут утворюють радіуси Землі, проведені до двох даних точок?
Розв’язання
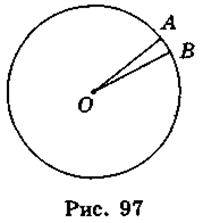
Нехай ОА = ОВ = 6370 км, lAB = 1 км (рис. 97). Оскільки 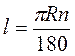 , то маємо
, то маємо 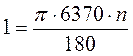 ; 180 = 6370n, звідси n =
; 180 = 6370n, звідси n = 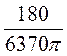
 0,009.
0,009.
Отже, шуканий кут дорівнює n° = 0,009° = 0,009 • 60′ = 0,54′ = 0,54 • 60″  32″.
32″.
Відповідь.  32″.
32″.
9. За даною хордою а знайдіть довжину її дуги, якщо градусна міра дуги дорівнює 120°.
Розв’язання
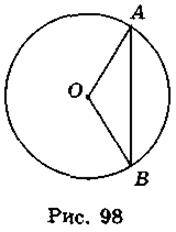
Нехай АВ = а,  AOB = 120° (рис. 98), OA = OB = R. За теоремою косинусів маємо:
AOB = 120° (рис. 98), OA = OB = R. За теоремою косинусів маємо:
АВ2 = АО2 + ВO2 – 2 • АО • BO • cos  AOB;
AOB;
A2 = 2R2 – 2R2 cos120°; a2 = 2R2 + R2; a2 = 3R2; R2 = 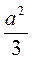 ; R =
; R = 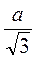 .
.
Тоді 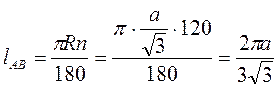 .
.
Відповідь. 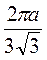 .
.
10. За довжиною дуги l знайдіть її хорду, якщо дуга становить 120°.
Розв’язання
Оскільки 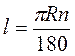 , то
, то 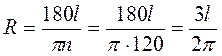 . За теоремою косинусів (рис. 98): АВ2 = АО2 + ВО2 – 2 • АО • BO • cos
. За теоремою косинусів (рис. 98): АВ2 = АО2 + ВО2 – 2 • АО • BO • cos  AOB = R2 + R2 + R2 = 3R2 = 3
AOB = R2 + R2 + R2 = 3R2 = 3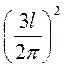 . Звідси АВ =
. Звідси АВ = 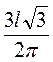 .
.
Відповідь. 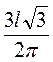 .
.
IV. Самостійна робота
Самостійну роботу навчального характеру можна провести за посібником [14], тест 7 “Довжина кола. Довжина дуги кола”.
V. Домашнє завдання
1. Вивчити формули довжини кола і довжини дуги кола. 2. Розв’язати задачі. 1) Обчисліть довжину кола, якщо радіус дорівнює: а) 10 м; б) 15 м. 2) Знайдіть довжину дуги кола радіуса 1 см, яка відповідає центральному куту, що становить:
А) 45°; б) 120°.
3) Знайдіть градусну міру центрального кута, якщо відповідна йому дуга становить:
А) 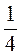 ; б)
; б) 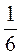 ; в)
; в) 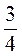 .
.
4) За даним колом радіуса R = 1 м знайдіть довжину дуги, яка відповідає центральному куту, що становить:
А) 30°; б) 45°45′.
VI. Підбиття підсумків уроку
Завдання класу
1. Чому дорівнює відношення довжини кола до діаметра? 2. Запишіть формули для знаходження:
А) довжини кола;
Б) довжини дуги кола, що відповідає куту n°.