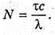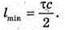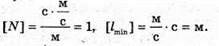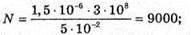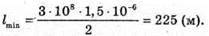ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ ТА ХВИЛІ
Вправа 23
1.
Дано: С = 1мкФ = 10-6 Ф L = 4 Гн Qм =100 мкКл = 10-4 Кл Q(t) – ?? І(t) – ? U(t) – ? Im – ? Um – ? | Розв’язання: Загальний вигляд рівняння, що описує коливання заряду на обкладинках конденсатора: q(t) = qm cos ωt. Циклічну частоту коливань знайдемо з формули Томсона:
Оскільки Сила струму це похідна заряду від гасу. Отже, і(t) = q'(t) = – qm ω sin ωt = – Im sin ωt. Звідси В коливальному контурі відбуваються перетворення енергії електричного поля в енергію магнітного поля, і навпаки. Згідно з законом збереження енергії: Звідси Різниця потенціалів на обкладинках конденсатора змінюється за законом: Перевіримо одиниці фізичних величин
Знайдемо числові значення.
Іm = 10-4 х 500 = 0,05 (А);
Q(t) = 10-4 cos 500t; і(t) = -0,05 sin 500t; u(t) =100 cos 500t. Відповідь: амплітудне значення сили струму |
2.
Дано: L = 0,2 мГн = 2 х 10-4 Гн C1 = С2 = 4 мкФ = 4 x 10-6 Ф Im = 0,1 А Т – ? Qm – ? Um1- ? Um2- ? | Розв’язання: Період коливань у контурі визначається з формули Томсона: Оскільки конденсатори з’єднані послідовно, то їх загальна ємність дорівнює: Отже Заряд на обкладинках конденсаторів, з’єднаних послідовно, однаковий: Qm1 = qm2 = qm Максимальний заряд пов’язаний з амплітудним значенням сили струму співвідношенням: Im= qm ω,
З визначення електричної ємності: Отже, Перевіримо одиниці фізичних величин:
[qm] = А · с = Кл; Знайдемо числові значення:
Відповідь: період коливань у контурі 12,56 х 10π-5 с, максимальне значення заряду кожного конденсатора 2 мкКл, максимальна напруга на кожному конденсаторі 0,5 В. |
3.
Дано: L С Um
I – ? | Розв’язання: В коливальному контурі відбуваються перетворення енергії електричного поля в енергію магнітного поля і навпаки. Згідно з законом збереження енергії:
Отже, Відповідь: сила струму буде |
4.
Дано: С = 10-5 Ф L = 0,1 Гн T = 5 T Um = 0,95Um0 R – ? | Розв’язання: В реальному коливальному контурі коливання затухають, оскільки частина енергії електромагнітного поля при кожному коливанні перетворюється у внутрішню енергію активного опору: Вважаючи, що амплітуда сили струму не змінюється, знайдемо кількість теплоти, що виділилася при проходженні струму, із закону Джоуля – Ленца: Q = I2Rt = 5 I2RT. Діюче значення сили струму Період власних коливань у коливальному контурі визначимо з формули Томсона. Амплітудне значення сили струму пов’язане з максимальним значенням напруги співвідношенням:
Тоді Отже, Звідси Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: активний опір контуру 0,32 Ом. |
5.
Дано: С = 10 мкФ = 10-5 Ф U = 400 В
Q – ? | Розв’язання: В реальному коливальному контурі коливання затухають, оскільки частина енергії електромагнітного поля перетворюється у теплову енергію: W0= W + Q, Отже, Q = W0- W. Згідно з законом збереження енергії: енергія електромагнітного поля дорівнює максимальній енергії електричного поля: Отже, Перевіримо одиницю фізичних величин:
Знайдемо числове значення:
Відповідь: в контурі виділиться 0,6 Дж теплоти. |
6.
Дано: L = 0,2 Гн Іm = 40 мА = 4 х 10-2 А
Wм – ? We – ? | Розв’язання: Енергія магнітного поля котушки: В коливальному контурі відбуваються перетворення енергії електричного поля в енергію магнітного поля і навпаки. Згідно з законом збереження енергії, повна енергія контуру дорівнює: W =Wе + Wм. Оскільки
Перевіримо одиниці фізичних величин: [We] = Дж.
Знайдемо числові значення:
Wе = З х 40 х 10 -6 =120 х 10 -6 (Дж) = 120 (мкДж). Відповідь: енергія електричного поля конденсатора 120 мкДж, енергія магнітного поля котушки 40 мкДж. |
Вправа 24
1.
Дано: V1 = 6 МГц = 6 х 106 Гц λ2= 150 м L1 = L2 = L
| Розв’язання: Довжина хвилі пов’язана з частотою електромагнітних коливань співвідношенням: Вважаючи, що швидкість електромагнітної хвилі дорівнює швидкості світла у вакуумі, можемо записати: Згідно з формулою Томсона: Оскільки частота коливань обернено пропорційна періоду, то:
Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: ємність конденсатора потрібно збільшити в 9 разів. |
2.
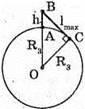
Дано: H = 25 м С = 3 • 108м/с R3 = 6,4 х106 м Lmax – ? Vімп – ? | Розв’язання:
Вважаючи, що радіохвилі не огинають Землю, знайдемо максимальну відстань виявлення цілі із трикутника ΔОВС. Оскільки ΔABC – прямокутний, то скористаємося теоремою Піфагора: ВС = lmax, OB = R3 + h, ОС = R3, Тоді Оскільки 2R3h >> h2, то Посланий імпульс має повернутися до посилання наступного. Оскільки шлях, який подолає імпульс, вдвічі більший за максимальну відстань виявлення цілі, а сигнал розповсюджується зі швидкістю світла, то Tімп – період посилання імпульсів. Період – це величина обернена до частоти: Отже, Перевіримо одиниці фізичних величин:
Знайдемо числові. значення:
Відповідь: максимальна відстань виявлення цілі 18 км; частота випускання імпульсів 8333 с_1. |
3.
Дано: λ = 5 см = 5 x 10 – 2 м τ = 1,5 мкс = 1,5 x 10-6 c
N – ? Lmin – ? | Розв’язання: Оскільки частота це кількість імпульсів за одиницю часу, то Вважаючи, що радіосигнал розповсюджується зі швидкістю світла, знайдемо частоту електромагнітної хвилі зі співвідношення: с = λν, Відбитий сигнал має повернутися не раніше, ніж закінчиться час випромінювання. Оскільки шлях, який подолає імпульс, вдвічі більший зі мінімальну відстань Виявлення цілі, то 2lmin = сτ, Перевіримо одиниці фізичних величин:
Знайдемо числові значення:
Відповідь: в кожному імпульсі міститься 9000 коливань, мінімальна дальність виявлення цілі 225 м. |
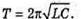
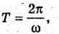 то
то 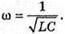
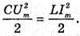
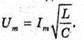
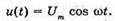
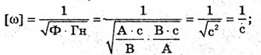
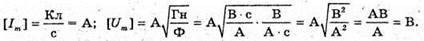
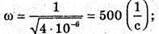
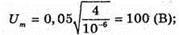
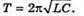
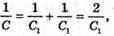
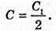
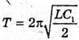
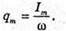 Оскільки
Оскільки 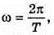 то
то 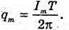
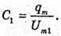
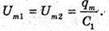
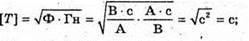
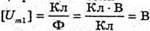
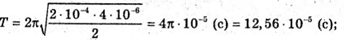
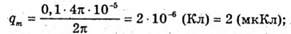
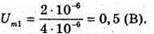
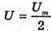
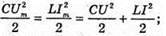
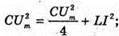
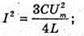
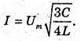
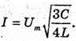
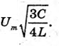
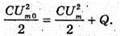
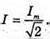
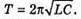
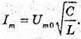
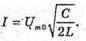
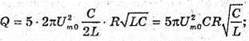
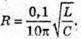
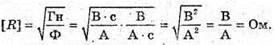
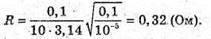
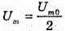
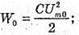
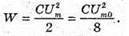
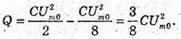
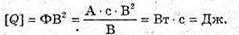
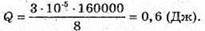
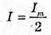
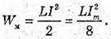
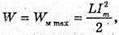 то
то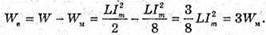
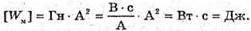
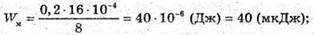
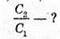
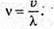
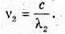
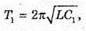
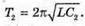
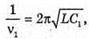
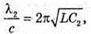
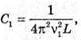
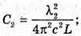
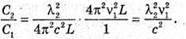
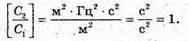
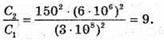
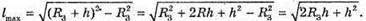
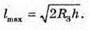
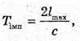 Де
Де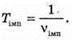
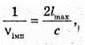
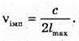
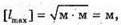
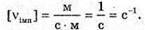
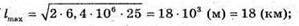
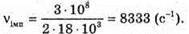
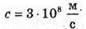
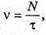 N = τν.
N = τν.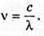 Отже,
Отже,